ГАУССА - ЛАПЛАСА РАСПРЕДЕЛЕНИЕ

одно из названий нормального распределения, к-рое наряду с другими названиями (Гаусса закон, гауссовское распределение, второй закон Лапласа, Лапласа- Гаусса распределение и т. д.) связывает историю открытия и первых приложений распределения к различным задачам теории вероятностей с именами К. <Гаусса (C.Gauss) и П. Лапласа (P. Laplace). Нормальное распределение появилось у К. Гаусса (1809) и П. Лапласа (1812) в связи с исследованиями по ошибок теории и наименьших квадратов методу. Так, в развитой К. Гауссом для задач астрономии и геодезии теории ошибок наблюдений плотность вероятностей случайных ошибок выражалась функцией

(см. Гаусса закон). П. Лаплас, кроме того, получил интеграл (функцию Лапласа)

как приближенное значение (при больших га) вероятности того, что число успехов в писпытаниях Бер-нулли с вероятностью успеха рбудет заключено в пределах и (так наз. предельная формула Лапласа). Однако соотношение, где нормальное распределение появляется как предельная форма биномиального с 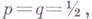было найдено еще А. Муавром (A. Moivre, 1733).

Лит.:[1] Гаусс К. Ф., Избр. геодезические соч., пер. с лат. и нем., т. 1, М., 1957, с. 89-109; [2] Lар1асе P. S., Theorie analitique des probabilites, P., 1812; [3] Тоdhunter I., A history of the mathematical theory of probability, [N. Y.], 1949. А. В. Прохоров.