Неприводимый многочлен — многочлен, неразложимый на нетривиальные (неконстантные) многочлены. Неприводимые многочлены являются неприводимыми элементами кольца многочленов. Содержание 1 Определение 2 Свойства 3 Примеры … Википедия
НЕПРИВОДИМЫЙ МНОГОЧЛЕН — многочлен, не разлагающийся на множители более низкой степени. Возможность разложить многочлен на множители (и свойство неприводимости) зависит от того, какие числа допускаются в качестве коэффициента многочлена. Так, многочлен х3 + 2 неприводим … Большой Энциклопедический словарь
неприводимый многочлен — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN irreducible polynominal … Справочник технического переводчика
неприводимый многочлен — многочлен, не разлагающийся на множители более низкой степени. Возможность разложить многочлен на множители (и свойство неприводимости) зависит от того, какие числа допускаются в качестве коэффициента многочлена. Так, многочлен х3 + 2 неприводим … Энциклопедический словарь
НЕПРИВОДИМЫЙ МНОГОЧЛЕН — многочлен от ппеременных над полем к, являющийся простым элементом кольца т. е. непредставимый в виде произведения , где gи h многочлены с коэффициентами из k, отличные от константы (неприводимость над k). Многочлен наз. абсолютно неприводимым,… … Математическая энциклопедия
НЕПРИВОДИМЫЙ МНОГОЧЛЕН — многочлен, не разлагающийся на множители более низкой степени. Возможность разложить многочлен на множители (и. свойство неприводимости) зависит от того, какие числа допускаются в качестве коэф. многочлена. Так, многочлен х3 + 2 неприводим, если… … Естествознание. Энциклопедический словарь
Многочлен — Запрос «Полином» перенаправляется сюда; см. также другие значения. Многочлен (или полином) от n переменных это конечная формальная сумма вида , где есть набор из целых неотрицательных чисел (называется мультииндекс), число… … Википедия
Многочлен Лорана — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия
Многочлен — полином, выражение вида Axkyl…..wm + Bxnyp…..wq + …… + Dxrts…..wt, где х, у, ..., w переменные, а А, В, ..., D (коэффициенты М.) и k, l, ..., t (показатели степеней целые неотрицательные числа) постоянные. Отдельные… … Большая советская энциклопедия
МНОГОЧЛЕН — полином, выражение вида где переменные, а А, В, ..., D (коэффициент ы М.) и x, y, .. ., w (показатели степеней целые неотрицательные числа) постоянные. Отдельные слагаемые вида наз. членами М. Порядок членов, а также порядок множителей в каждом… … Математическая энциклопедия
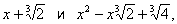если в качестве коэффициентов брать любые действительные числа, и в произведение трёх множителей
если коэффициентами будут числа комплексные. В общем случае понятие неприводимости определяется для многочленов с коэффициентами, принадлежащими произвольному полю (см. Поле алгебраическое). Часто Н. м. называют многочлен с рациональными коэффициентами, не разлагающийся на множители более низкой степени также с рациональными коэффициентами.Лит.: Курош А. Г., Курс высшей алгебры, 9 изд., М., 1968.