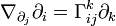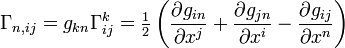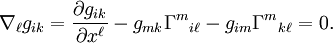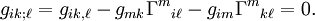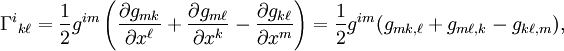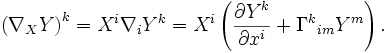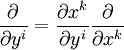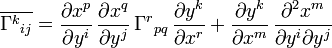- Кристоффеля символ
-
Символы Кристоффеля являются координатными выражениями аффинной связности, в частности связности Леви-Чивиты. Названы в честь Элвина Бруно Кристоффеля (1829—1900),
Символы Кристоффеля используются в дифференциальной геометрии, общей теории относительности и близких к ней теориях гравитации.
Символы Кристоффеля появляются в координатном выражении тензора кривизны. При этом сами символы тензорами не являются.
Ниже используется правило суммирования Эйнштейна, то есть по повторяющимся индексам подразумевается суммирование.
Содержание
Символы Кристоффеля первого и второго рода
Символы Кристоффеля второго рода
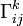 можно определить как коэффициенты разложения ковариантной производной координатных векторов
можно определить как коэффициенты разложения ковариантной производной координатных векторов 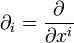 по базису:
по базису:Символы Кристоффеля первого рода
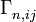
Выражение через метрический тензор
Символы Кристоффеля связности Леви-Чивита для карты xi могут быть определены из отсутствия кручения, то есть
- Γijk = Γikj.
и того условия, что ковариантная производная метрического тензора
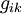 равна нулю:
равна нулю:Для сокращения записи символ набла
 и символы частных производных часто опускаются, вместо них перед индексом, по которому производится дифференцирование, ставится точка с запятой «;» в случае ковариантной и запятая ", " в случае частной производной. Таким образом, выражение выше можно также записать как
и символы частных производных часто опускаются, вместо них перед индексом, по которому производится дифференцирование, ставится точка с запятой «;» в случае ковариантной и запятая ", " в случае частной производной. Таким образом, выражение выше можно также записать какЯвные выражения для символов Кристоффеля второго рода получаются, если сложить это уравнение и другие два уравнения, которые получаются циклической перестановкой индексов:
где
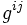 — контравариантное представление метрики, которое есть матрица, обратная к
— контравариантное представление метрики, которое есть матрица, обратная к 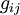 , находится путём решения системы линейных уравнений
, находится путём решения системы линейных уравнений 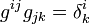 .
.Связь с безындексными обозначениями
Формальные, безындексные определения связности абстрагируются от конкретной системы координат и поэтому более предпочтительны при доказательстве математических теорем.
Пусть X и Y — векторные поля с компонентами
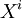 и
и 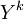 . Тогда k-я компонента ковариантной производной поля Y по отношению к X задается выражением
. Тогда k-я компонента ковариантной производной поля Y по отношению к X задается выражениемУсловие отсутствия кручения у связности, :
![\nabla_X Y - \nabla_Y X = [X,Y]\](/pictures/wiki/files/100/d648cf4c00e22c528c0c716bfc400b2d.png) , эквивалентно симметричности символов Кристоффеля по двум нижним индексам:
, эквивалентно симметричности символов Кристоффеля по двум нижним индексам:- Γijk = Γikj.
Замена координат
Несмотря на то, что символы Кристоффеля записываются в тех же обозначениях, что и компоненты тензоров, они не являются тензорами, потому что не преобразуются как тензоры при переходе в новую систему координат. В частности, выбором координат в окрестности любой точки символы Кристоффеля могут быть локально сделаны равными нулю (или обратно ненулевыми), что невозможно для тензора.
При замене переменных
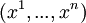 на
на 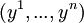 , базисные векторы преобразуются ковариантно,
, базисные векторы преобразуются ковариантно,откуда следует формула преобразования символов Кристоффеля:
Черта означает систему координат y. Таким образом, символы Кристоффеля не преобразуются как тензор. Они представляют собой более сложный геометрический объект в касательном пространстве с нелинейным законом преобразования от одной системы координат к другой.
Примечание. Можно заметить, например, из определения, что первый индекс является тензорным, то есть по нему символы Кристоффеля преобразуются как тензор.
Символы Кристоффеля в различных системах координат
Пользуясь выражением символа через метрический тензор, либо преобразованием координат, можно получить значения их в любой системе координат. В механике и физике чаще всего используются ортогональные криволинейные системы координат. В этом случае символы Кристоффеля с равными коэффициентами выражаются через коэффициенты Ламе (диагональные элементы метрического тензора) Hβ, а все остальные равны нулю.
Символы Кристоффеля первого рода выражаются так:
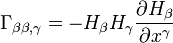 , при
, при 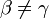 .
.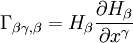 .
.
Символы Кристоффеля второго рода:
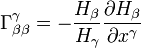 , при
, при 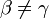 .
.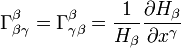
Ниже приведены значения для распространённых систем координат:
- В декартовой системе координат
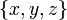 :
: 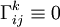 , поэтому ковариантная производная совпадает с частной производной.
, поэтому ковариантная производная совпадает с частной производной. - В цилиндрической системе координат
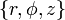 :
: 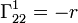 ,
, 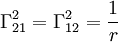 . Остальные равны нулю.
. Остальные равны нулю. - В сферической с.к.
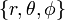 :
: 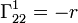 ,
, 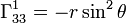 ,
, 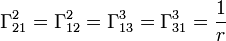 ,
, 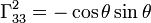 ,
, 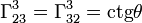 . Остальные равны нулю.
. Остальные равны нулю.
См. также
Другие величины, широко используемые в тензорном анализе
Литература
- Димитриенко Ю.И. Тензорное исчисление. — М.: Высшая школа, 2001. — 575 с. — ISBN 5-06-004155-7
- Победря Б.Е. Лекции по тензорному анализу. — Издательство Московского университета, 1974. — 206 с.
Ссылки
Wikimedia Foundation. 2010.