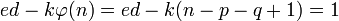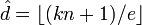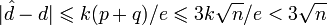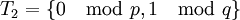- Криптосистема Ривеста — Шамира — Адельмана
-
RSA (буквенная аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический алгоритм с открытым ключом.
RSA стал первым алгоритмом такого типа, пригодным и для шифрования, и для цифровой подписи. Алгоритм используется в большом числе криптографических приложений.
Содержание
История
Опубликованная в ноябре 1976 года статья Уитфилда Диффи и Мартина Хеллмана «Новые направления в криптографии» перевернула представление о криптографических системах, заложив основы криптографии с открытым ключом. Разработанный впоследствии алгоритм Диффи-Хеллмана-Меркле позволял двум сторонам получить общий секретный ключ, используя незащищенный канал связи. Однако этот алгоритм не решал проблему аутентификации. Без дополнительных средств, один из пользователей не мог быть уверен, что он обменялся ключами именно с тем пользователем, который ему был нужен.
Изучив эту статью, трое ученых Рональд Райвест (Ronald Linn Rivest), Ади Шамир (Adi Shamir) и Леонард Адлеман (Leonard Adleman) из Массачусетского Технологического Института (MIT) приступили к поискам математической функции, которая бы позволяла реализовать сформулированную Уитфилдом Диффи и Мартином Хеллманом модель криптографической системы с открытым ключом. После работы над более чем 40 возможными вариантами, им удалось найти алгоритм, основанный на различии в том, насколько легко находить большие простые числа и насколько сложно раскладывать на множители произведение двух больших простых чисел, получивший впоследствии название RSA. Система была названа по первым буквам фамилий её создателей.
Описание RSA было опубликовано в августе 1977 года в журнале Scientific American. Авторы RSA поддерживали идею её активного распространения. В свою очередь, Агентство национальной безопасности (США), опасаясь использования этого алгоритма в негосударственных структурах, на протяжении нескольких лет безуспешно требовало прекращения распространения системы. Ситуация порой доходила до абсурда — например, когда программист Адам Бек(Adam Back) описал алгоритм RSA на языке
В 1983 году MIT был выдан патент 4405829 США, срок действия которого истёк 21 сентября 2000 года.[1]
В 1977 году создателями RSA была зашифрована фраза «The Magic Words are Squeamish Ossifrage» («Волшебные слова — это брезгливый ягнятник»). За расшифровку была обещана награда в 100 долларов США. Лишь в конце 1995 года удалось практически реализовать раскрытие шифра RSA для 500-значного ключа. На протяжении полугода более 600 добровольцев жертвовали процессорное время 1600 машин (две из которых были факс-машинами). Координирование проходило через Интернет, и это был один из первых подобных проектов распределённых вычислений. Полученную награду победители пожертвовали в фонд свободного программного обеспечения.
В декабре 1997 года была обнародована информация, согласно которой британский математик Клиффорд Кокс (Clifford Cocks), работавший в центре правительственной связи (GCHQ) Великобритании, описал аналогичную систему в 1973 году, несколькими месяцами позже в 1974 году Малькольм Вильямсон изобрел математический алгоритм, основанный на коммутативности возведения в степень, аналогичный алгоритму Диффи-Хеллмана-Меркле.
Описание алгоритма
Введение
Криптографические системы с открытым ключом используют так называемые однонаправленные функции, которые обладают следующим свойством:
- Если
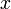 известно, то
известно, то  вычислить относительно просто
вычислить относительно просто - Если известно
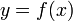 , то для
, то для 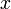 нет простого пути вычисления
нет простого пути вычисления
Под однонаправленностью понимается не теоретическая однонаправленость, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени.
В основу криптографической системы с открытым ключом RSA положена задача умножения и разложения простых чисел на множители, которая является вычислительно однонаправленной задачей.(доп.информация см. тест простоты, факторизация)
В криптографической системе с открытым ключом каждый участник располагает как открытым ключом (public key), так и секретным ключом (secret key). Каждый ключ — это часть информации. В криптографической системе RSA каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и секретный ключ самостоятельно. Секретный ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их. Открытый и секретный ключи каждого участника обмена сообщениями образуют «согласованную пару» в том смысле, что они являются взаимно обратными, т.е
 сообщения
сообщения 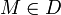 , где
, где 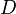 -множество допустимых сообщений.
-множество допустимых сообщений.
 открытого и секретного ключа
открытого и секретного ключа 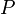 и
и 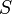
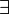 соответствующие функции
соответствующие функции 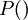 и
и 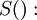
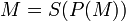

Алгоритм создания открытого и секретного ключей
- Выбираются два случайных простых числа
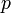 и
и  заданного размера (например, 512 битов каждое).
заданного размера (например, 512 битов каждое). - Вычисляется их произведение
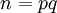
- Вычисляется значение функция Эйлера от числа n:
- Выбирается целое число
 , взаимно простое со значением функции
, взаимно простое со значением функции 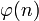 . Обычно в качестве e берут простые числа, содержащие небольшое количество единичных битов в двоичной записи, например, простые числа Ферма 17, 257, или 65537.
. Обычно в качестве e берут простые числа, содержащие небольшое количество единичных битов в двоичной записи, например, простые числа Ферма 17, 257, или 65537. - Вычисляется число d, мультипликативно обратное к числу e по модулю
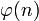 , т.е число, удовлетворяющее сравнению:
, т.е число, удовлетворяющее сравнению:
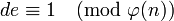 ; то есть
; то есть 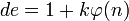 , где k любое натуральное число (0, 1, 2…).
, где k любое натуральное число (0, 1, 2…).
- Пара
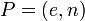 публикуется в качестве открытого ключа RSA (RSA public key).
публикуется в качестве открытого ключа RSA (RSA public key). - Пара
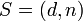 играет роль секретного ключа RSA (RSA secret key) и держится в секрете.
играет роль секретного ключа RSA (RSA secret key) и держится в секрете.
Число
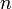 называется модулем, а числа
называется модулем, а числа  и
и 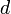 — открытой и секретной экспонентами, соответственно.
— открытой и секретной экспонентами, соответственно.Шифрование и расшифрование
Схема RSA
Предположим, сторона
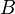 хочет послать стороне
хочет послать стороне 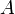 сообщение
сообщение  .
.Сообщением являются целые числа лежащие от
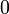 до
до 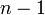 , т.е
, т.е 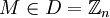 .
.
Алгоритм:
- Взять открытый ключ
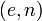 стороны
стороны 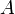
- Взять открытый текст

- Передать шифрованное сообщение:

Алгоритм:
- Принять зашифрованное сообщение
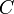
- Применить свой секретный ключ
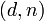 для расшифровки сообщения:
для расшифровки сообщения:
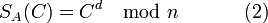
Корректность схемы RSA
- Уравнения
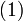 и
и  , на которых основана схема RSA, определяют взаимно обратные преобразования множества
, на которых основана схема RSA, определяют взаимно обратные преобразования множества 
ДоказательствоДействительно, для
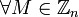
Докажем, что
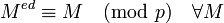 .
.Возможны два случая:
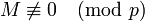 .
.
Поскольку числа
 и
и 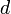 являются взаимно обратными относительно умножения по модулю
являются взаимно обратными относительно умножения по модулю  , т.e
, т.e-
 для некоторого целого
для некоторого целого 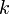 , тогда
, тогда
где второе тождество следует из теоремы Ферма.
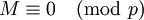 , тогда
, тогда 
Таким образом, при всех
 выполняется равенство
выполняется равенствоАналогично можно показать, что
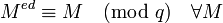 .
.Таким образом, из Китайской теоремы об остатках
Пример
Этап Описание операции Результат операции Генерация ключей выбрать два простых числа 
вычислить модуль 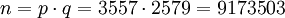
вычислить функцию Эйлера 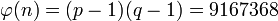
выбрать открытый показатель 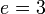
вычислить секретный показатель 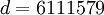
опубликовать открытый ключ 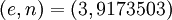
сохранить секретный ключ 
Шифрование выбрать открытый текст 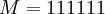
вычислить шифротекст 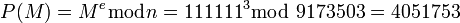
Расшифрование вычислить исходное сообщение 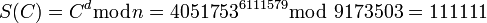
Цифровая подпись
Система RSA может использоваться не только для шифрования, но и для цифровой подписи.
Предположим, что стороне
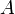 нужно отправить стороне
нужно отправить стороне 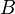 ответ
ответ 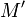 , подтверждённый цифровой подписью.
, подтверждённый цифровой подписью.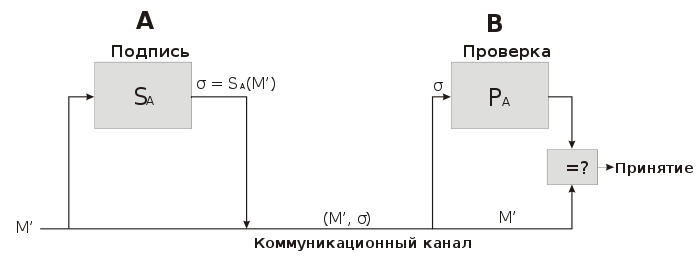
Алгоритм:
- Взять открытый текст
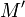
- Создать цифровую подпись
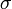 с помощью своего секретного ключа
с помощью своего секретного ключа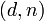
- Передать пару
 , состоящую из сообщения и подписи.
, состоящую из сообщения и подписи.
Алгоритм:
- Принять пару

- Взять открытый ключ
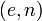 стороны
стороны 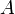
- Проверить подлинность подписи:
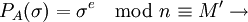 подпись верная
подпись вернаяПоскольку цифровая подпись обеспечивает как аутентификацию автора сообщения, так и подтверждение целостности содержимого подписанного сообщения, она служит аналогом подписи, сделанной от руки в конце рукописного документа.
Важное свойство цифровой подписи заключается в том, что её может проверить каждый, кто имеет доступ к открытому ключу ее автора. Один из участников обмена сообщениями после проверки подлинности цифровой подписи может передать подписанное сообщение ещё кому-то, кто тоже в состоянии проверить эту подпись. Например, сторона
 может переслать стороне
может переслать стороне  электронный чек. После того как сторона
электронный чек. После того как сторона  проверит подпись стороны
проверит подпись стороны 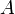 на чеке, она может передать его в свой банк, служащие которого также имеют возможность проверить подпись и осуществить соответствующую денежную операцию.
на чеке, она может передать его в свой банк, служащие которого также имеют возможность проверить подпись и осуществить соответствующую денежную операцию.Заметим, что подписанное сообщение
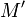 не зашифровано. Оно пересылается в исходном виде и его содержимое не защищено. Путём совместного применения представленных выше схем шифрования и цифровой подписи в системе RSA можно создавать сообщения, которые будут и зашифрованы, и содержать цифровую подпись. Для этого автор сначала должен добавить к сообщению свою цифровую подпись, а затем — зашифровать получившуюся в результате пару(состоящую из самого сообщения и подписи к нему) с помощью открытого ключа принадлежащего получателю. Получатель расшифровывает полученное сообщение с помощью своего секретного ключа. Если проводить аналогию с пересылкой обычных бумажных документов, то этот процесс похож на то, как если бы автор документа поставил под ним свою печать, а затем положил его в бумажный конверт и запечатал, с тем чтобы конверт был распечатан только тем человеком, кому адресовано сообщение.
не зашифровано. Оно пересылается в исходном виде и его содержимое не защищено. Путём совместного применения представленных выше схем шифрования и цифровой подписи в системе RSA можно создавать сообщения, которые будут и зашифрованы, и содержать цифровую подпись. Для этого автор сначала должен добавить к сообщению свою цифровую подпись, а затем — зашифровать получившуюся в результате пару(состоящую из самого сообщения и подписи к нему) с помощью открытого ключа принадлежащего получателю. Получатель расшифровывает полученное сообщение с помощью своего секретного ключа. Если проводить аналогию с пересылкой обычных бумажных документов, то этот процесс похож на то, как если бы автор документа поставил под ним свою печать, а затем положил его в бумажный конверт и запечатал, с тем чтобы конверт был распечатан только тем человеком, кому адресовано сообщение.Скорость работы алгоритма RSA
Поскольку генерация ключей происходит значительно реже операций, реализующих шифрование, расшифрование, а также создание и проверку цифровой подписи, задача вычисления
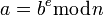 представляет основную вычислительную сложность. Эта задача может быть разрешена с помощью алгоритма быстрого возведения в степень. Таким образом для вычисления
представляет основную вычислительную сложность. Эта задача может быть разрешена с помощью алгоритма быстрого возведения в степень. Таким образом для вычисления 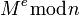 требуется
требуется 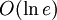 операций умножения по модулю.Доказательство
операций умножения по модулю.Доказательство- представим
 в двоичной системе счисления:
в двоичной системе счисления:
-
-
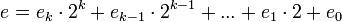 , где
, где 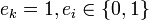
-
- положим
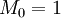 и затем для
и затем для  вычислим
вычислим
- найденное
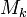 и будет искомым значением
и будет искомым значением 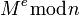
Т.к каждое вычисление на шаге 2 требует не более трёх умножений по модулю
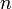 и этот шаг выполняется
и этот шаг выполняется 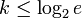 раз, то сложность алгоритма может быть оценена величиной
раз, то сложность алгоритма может быть оценена величиной 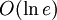 .
.Чтобы проанализировать время выполнения операций с открытым и секретным ключами, предположим, что открытый ключ
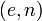 и секретный ключ
и секретный ключ 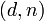 удовлетворяют соотношениям
удовлетворяют соотношениям 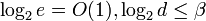 . Тогда в процессах их применения выполнятся соответственно
. Тогда в процессах их применения выполнятся соответственно 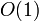 и
и 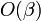 умножений по модулю.
умножений по модулю.Таким образом время выполнения операций растёт с увеличением количества ненулевых битов в двоичном представлении открытой экспоненты e. Чтобы увеличить скорость шифрования, значение e часто выбирают равным 17, 257 или 65537 — простым числам, двоичное представление которых содержит лишь две единицы: 17 = 0x11, 257 = 0x101, 65537 = 0x10001 (простые числа Ферма).
По эвристическим оценкам длина секретной экспоненты d, нетривиальным образом зависящей от открытой экспоненты e и модуля n, с большой вероятностью близка к длине n. Поэтому расшифрование данных идёт медленнее чем шифрование, а проверка подписи быстрее чем подписание.
Алгоритм RSA намного медленнее чем блочного шифрования. Программная реализация DES работает быстрее, по крайней мере, в 100 раз и от 1000 до 10 000 — в аппаратной реализации (в зависимости от конкретного устройства).
Криптоанализ RSA
На 2009 год система шифрования на основе RSA считается надёжной, начиная с размера
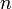 в 1024 бита.
в 1024 бита.Зная разложение модуля
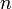 на произведение двух простых чисел, противник может легко найти секретную экспоненту
на произведение двух простых чисел, противник может легко найти секретную экспоненту 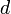 и тем самым взломать RSA. Однако на сегодняшний день самый быстрый алгоритм факторизации — решето обобщённого числового поля (General Number Field Sieve), скорость которого для k-битного целого числа составляет
и тем самым взломать RSA. Однако на сегодняшний день самый быстрый алгоритм факторизации — решето обобщённого числового поля (General Number Field Sieve), скорость которого для k-битного целого числа составляет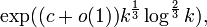 для некоторого
для некоторого 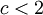 ,
,не позволяет разложить большое целое за приемлемое время. Будем рассматривать возможные атаки на RSA, которые позволяют взломать эту систему, не используя прямого разложения модуля n на произведение двух простых чисел.
Элементарные атаки
Рассмотрим несколько атак связанных с неправильным использованием алгоритма RSA.
Генерация простых чисел
На случайные простые числа
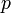 и
и  накладываются следующие дополнительные ограничения:
накладываются следующие дополнительные ограничения: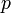 и
и  не должны быть слишком близки друг к другу, иначе можно будет их найти, используя метод факторизации Ферма. Однако, если оба простых числа
не должны быть слишком близки друг к другу, иначе можно будет их найти, используя метод факторизации Ферма. Однако, если оба простых числа 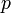 и
и  были сгенерированы независимо, то это ограничение с огромной вероятностью автоматически выполняется.
были сгенерированы независимо, то это ограничение с огромной вероятностью автоматически выполняется.- Необходимо выбирать «сильные» простые числа, чтобы нельзя было воспользоваться p-1 методом Полларда.
Схема с общим модулем n
Начальные данные: Чтобы избежать генерирования различных модулей
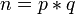 для каждого пользователя, защищённый сервер использует единый n для шифрования всех сообщений. Сторона
для каждого пользователя, защищённый сервер использует единый n для шифрования всех сообщений. Сторона 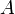 использует этот сервер для получения сообщения
использует этот сервер для получения сообщения 
Задача: противник хочет расшифровать сообщение стороны
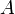 .
.Казалось бы, шифротекст
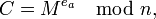 отправленный стороне
отправленный стороне 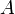 , не может быть расшифрован стороной
, не может быть расшифрован стороной 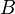 , если она не обладает секретным ключом
, если она не обладает секретным ключом 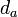 . Однако сторона
. Однако сторона 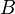 может использовать свои экспоненты
может использовать свои экспоненты 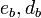 , чтобы разложить модуль
, чтобы разложить модуль 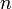 , и после этого, зная
, и после этого, зная 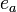 , вычислить секретную экспоненту
, вычислить секретную экспоненту  .
.Защита: для каждого пользователя должен использоваться свой модуль
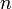 .
.Атака на подпись RSA в схеме с нотариусом
Начальные данные:
 — открытый ключ нотариуса. Противник получает отказ при попытке подписания нотариусом сообщения
— открытый ключ нотариуса. Противник получает отказ при попытке подписания нотариусом сообщения 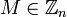
Задача: противник хочет получить подпись нотариуса на сообщении
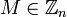 .
.Противник выбирает произвольное
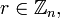 вычисляет
вычисляет  и отправляет это сообщение на подпись нотариусу.
и отправляет это сообщение на подпись нотариусу.Если нотариус подписывает это сообщение:
то противник, вычислив
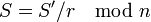 , получает подпись сообщения
, получает подпись сообщения  .
.Действительно,
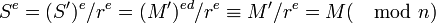
Защита: при подписи добавлять в сообщение некоторое случайное число (например, время).
Малые значения секретной экспоненты
Начальные данные: Чтобы увеличить скорость расшифрования (или создания цифровой подписи) было уменьшено число ненулевых битов двоичного представления секретной экспоненты
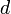 (см. скорость алгоритма RSA).
(см. скорость алгоритма RSA).Задача: вычислить секретную экспоненту
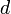 .
.В 1990 году Михаэль Винер (Michael J. Wiener) показал, что в случае малого значения d возможен взлом системы RSA, а именно:
Теорема Винера: Пусть n = pd, где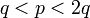
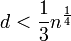 Тогда, если известно (n,e), где
Тогда, если известно (n,e), где  ,
то существует эффективный способ вычислить d.
,
то существует эффективный способ вычислить d.
Защита: Таким образом если n имеет размер 1024 бита, необходимо чтобы d был не менее 256 бит длиной.
Малые значения открытой экспоненты
Чтобы увеличить скорость шифрования и проверки цифровой подписи, используют малые значения открытой экспоненты
 . Наименьшее из них
. Наименьшее из них 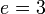 . Однако, чтобы повысить криптоустойчивость алгоритма RSA, рекомендовано использовать
. Однако, чтобы повысить криптоустойчивость алгоритма RSA, рекомендовано использовать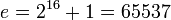 .
.Атака Хастада
Начальные условия: Сторона
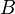 отсылает зашифрованное сообщение
отсылает зашифрованное сообщение  пользователям
пользователям 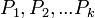 . Каждый пользователь имеет свой открытый ключ
. Каждый пользователь имеет свой открытый ключ 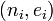 , причём
, причём 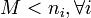 . Сторона
. Сторона  зашифровывает сообщение, используя поочерёдно открытый ключ каждого пользователя, и отсылает его соответствующему адресату. Противник прослушивает канал передачи и собирает
зашифровывает сообщение, используя поочерёдно открытый ключ каждого пользователя, и отсылает его соответствующему адресату. Противник прослушивает канал передачи и собирает 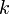 переданных шифротекстов.
переданных шифротекстов.Задача: противник хочет восстановить сообщение
 .
.Положим
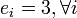 , тогда противник может восстановить
, тогда противник может восстановить  если
если 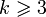 .Доказательство
.ДоказательствоДействительно, если противник получил
 , где
, гдеОчевидно
 взаимно просты, так как в противном случае хотя бы один из них был составным, что невозможно в системе RSA.Применяя китайскую теорему об остатках к
взаимно просты, так как в противном случае хотя бы один из них был составным, что невозможно в системе RSA.Применяя китайскую теорему об остатках к  , получим
, получим 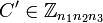 ,
,Поскольку
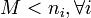 ,то
,то 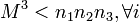 и
иТ.е противник может восстановить сообщение
 вычислив корень кубический из
вычислив корень кубический из 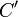 .
.В общем случае, если все открытые экспоненты равны
 , противник может восстановить
, противник может восстановить  при
при 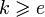 .
.Рассмотрим простейшую защиту от этой атаки. Пусть сообщение
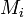 для каждого пользователя является некоторой фиксированной перестановкой исходного сообщения
для каждого пользователя является некоторой фиксированной перестановкой исходного сообщения  .К примеру
.К примеру-
-
-
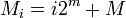 — сообщение для i-го пользователя.
— сообщение для i-го пользователя.
-
-
Хастад (Johan Hastad) показал, что даже в этом случае, противник может восстановить сообщение
 при достаточном количестве пользователей.
при достаточном количестве пользователей.Защита: Эта атака возможна только при малом значении открытой экспоненты
 , в этом случае криптостойкость системы RSA можно достигнуть, используя произвольную перестановку, а не фиксированную, пример которой был приведён выше.
, в этом случае криптостойкость системы RSA можно достигнуть, используя произвольную перестановку, а не фиксированную, пример которой был приведён выше.Атака Франклина-Рейтера
Начальные условия:
Имеются два сообщения
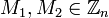 , причём
, причём-
-
-
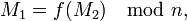 где
где ![f \in \mathbb{Z}_n[x]\,](/pictures/wiki/files/101/e144e01a9ba42e40092cf161b89b112f.png) некоторый открытый многочлен.
некоторый открытый многочлен.
-
-
Сторона
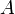 с открытым ключом
с открытым ключом  получает эти сообщения от стороны
получает эти сообщения от стороны 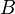 , которая просто зашифровывает сообщения
, которая просто зашифровывает сообщения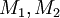 и передаёт полученные шифротексты
и передаёт полученные шифротексты 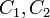 .
.Задача: Противник, зная
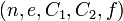 , хочет восстановить
, хочет восстановить 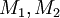 .
.Метью Франклин (Matthew K. Franklin) и Михаэль Рейтер (Michael K. Reiter) доказали, следующее утверждение:
Пусть 1) - открытый ключ системы RSA, причём
- открытый ключ системы RSA, причём 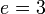 2)
2)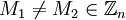 и
и 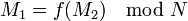 ,
для некоторого линейного многочлена
,
для некоторого линейного многочлена ![f=ax+b \in \mathbb{Z}_n[x] \,](/pictures/wiki/files/48/0a7c4c34c80d839e8751e5f65bb538c2.png) ,
, 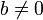 Тогда, зная
Тогда, зная 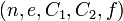 , противник может восстановить
, противник может восстановить 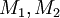 Доказательство
ДоказательствоДействительно, для произвольного
 :
: , является корнем многочлена
, является корнем многочленано,
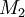 является также корнем многочлена
является также корнем многочлена-
-
-
![g_2(x)=x^e-C_2 \in \mathbb{Z}_n[x] \,](/pictures/wiki/files/50/2eb192cbbf92c1014a2a1f96d9da3599.png) .
.
-
-
Таким образом
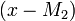 делит оба многочлена. И противник может использовать алгоритм Евклида, чтобы вычислить НОД
делит оба многочлена. И противник может использовать алгоритм Евклида, чтобы вычислить НОД 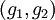 . Если результат окажется линейным многочленом, то
. Если результат окажется линейным многочленом, то 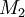 будет найдено.
будет найдено.Когда
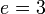 , НОД
, НОД 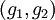 является линейным многочленом, и следовательно противник может эффективно вычислить сообщения
является линейным многочленом, и следовательно противник может эффективно вычислить сообщения 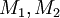 .
.Защита: при
 время взлома системы RSA пропорционально
время взлома системы RSA пропорционально 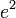 , поэтому данная атака может быть использована только при малых значениях открытой экспоненты.
, поэтому данная атака может быть использована только при малых значениях открытой экспоненты.Атака по частично известной секретной экспоненте
Начальные условия:
Противник знает часть двоичного представления секретной экспоненты
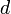 .
.Задача: восстановить
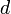 .
.Оказывается, что когда
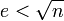 , эта атака возможна, а именно:
, эта атака возможна, а именно:Пусть
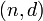 — секретный ключ системы RSA, где
— секретный ключ системы RSA, где 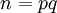 имеет размер
имеет размер 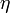 битов.
Тогда, зная
битов.
Тогда, зная 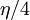 младших битов числа
младших битов числа 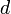 , противник может восстановить
, противник может восстановить 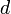 за время, пропорциональное
за время, пропорциональное 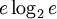
Возможность взлома системы RSA в случае, когда открытая экспонента
 мала, так же очевидна из следующих рассуждений:
мала, так же очевидна из следующих рассуждений:- из определения
 и
и 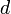 :
:
- Поскольку
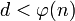 , то очевидно
, то очевидно 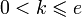 .
.
- При заданном
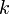 противник может легко вычислить
противник может легко вычислить
- Тогда при
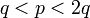
- Таким образом,
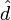 является хорошим приближением при
является хорошим приближением при 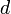 . Экспериментально показано, что в большинстве случаев старшие биты двоичного представления
. Экспериментально показано, что в большинстве случаев старшие биты двоичного представления 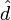 совпадают с соответствующими битами секретной экспоненты
совпадают с соответствующими битами секретной экспоненты 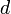 .
.
- Поскольку возможны только
 различных значений
различных значений 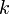 , противник может построить ряд, содержащий
, противник может построить ряд, содержащий  членов, для которого двоичное представление одного из его элементов совпадает со старшей половиной двоичного представления секретной экспоненты
членов, для которого двоичное представление одного из его элементов совпадает со старшей половиной двоичного представления секретной экспоненты 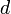 .
.
Защита: увеличение открытой экспоненты
 .
.Атака с помощью квантового компьютера
С помощью квантового компьютера, если он будет построен, можно будет взломать RSA, так как квантовый алгоритм Шора позволяет осуществить факторизацию больших чисел за достаточно короткое время. Разложив модуль n на простые множители, можно будет вычислить секретный показатель d.
Атаки, связанные с реализацией системы RSA
Атака по времени выполнения
Начальные условия:
Рассмотрим смарт-карту, микропроцессор которой подписывает сообщения, используя встроенный секретный ключ RSA.
Задача: противник хочет получить секретную экспоненту
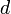 .
.Пол Кохер (Paul Kocher), предложил атаку, основанную на высокоточных замерах времени выполнения шифратором смарт-карты определенных операций. Рассмотрим эту атаку на примере системы RSA, использующей алгоритм быстрого возведения в степень:
Противник получает подписи смарт-карты для большого числа произвольных сообщений
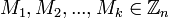 , и измеряет время генерации их подписей
, и измеряет время генерации их подписей  .
.В ходе атаки значение секретной экспоненты
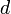 восстанавливается побитно, начиная с младшего бита:
восстанавливается побитно, начиная с младшего бита: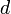 нечётное, поэтому
нечётное, поэтому  .
.- если
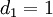 то микропроцессору смарт-карты необходимо произвести три умножения по модулю
то микропроцессору смарт-карты необходимо произвести три умножения по модулю 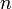 , в отличии от двух, необходимых при
, в отличии от двух, необходимых при 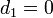 (см.алгоритм быстрого возведения в степень).Обозначим
(см.алгоритм быстрого возведения в степень).Обозначим 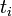 — время вычислений процессора для сообщения
— время вычислений процессора для сообщения 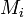 .
.
- Кохер показал, что когда
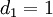 два ансамбля
два ансамбля  и
и 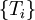 коррелируют.Однако в случае
коррелируют.Однако в случае 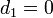 они независимы. Таким образом, прибегая к корреляционному анализу, противник может определить
они независимы. Таким образом, прибегая к корреляционному анализу, противник может определить  .
.
- аналогично можно определить
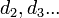 .
.
Заметим, что в случае малой открытой экспоненты
 может быть применена атака по частично открытой секретной экспоненте.В этом случае достаточно восстановить половину бит секретной экспоненты
может быть применена атака по частично открытой секретной экспоненте.В этом случае достаточно восстановить половину бит секретной экспоненты 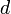 .
.Защита: необходимо добавлять соответствующую задержку таким образом, чтобы каждый шаг алгоритма быстрого возведения в степень занимал фиксированный период времени.
Атака при сбое аппаратной реализации RSA
Начальные условия:
Рассмотрим смарт-карту, микропроцессор которой подписывает сообщения, используя встроенный секретный ключ RSA. Микропроцессор карты использует китайскую теорему об остатках в целях ускорения процедуры подписи. Противник пытается вызвать сбой в вычислениях микропроцессора.
Задача: противник хочет вычислить модуль
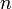 .
.Использование китайской теоремы об остатках, увеличивает скорость создания цифровой подписи.
- Действительно, вычислив
-
-
-
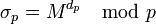 , где
, где 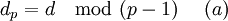
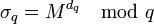 , где
, где 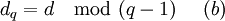
-
-
- можно получить подпись
-
-
-
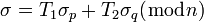 , где
, где 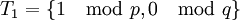
-
-
-
- Очевидно вычисления
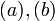 гораздо быстрее возведения в степень по модулю
гораздо быстрее возведения в степень по модулю 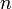 .
.
Пусть действия противника вызвали сбой, повлёкший за собой дефект одного бита подписи. Тогда по крайней мере одна из
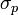 или
или 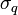 вычислена неправильно. Положим дефект содержится в
вычислена неправильно. Положим дефект содержится в 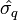 .
.В этом случае
однако
Таким образом противник может найти разложение
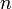 ,как результат поиска НОД
,как результат поиска НОД .
.Защита:
- при подписи добавлять в сообщение некоторое случайное число(например время).
- проверять подпись перед тем как её отправить.
Применение RSA
Система RSA используется для защиты программного обеспечения и в схемах цифровой подписи.
Также она используется в открытой системе шифрования симметричными алгоритмами.
Из-за низкой скорости шифрования (около 30 кбит/с при 512 битном ключе на процессоре 2 ГГц), сообщения обычно шифруют с помощью более производительных симметричных алгоритмов со случайным ключом (сеансовый ключ), а с помощью RSA шифруют лишь этот ключ. Такой механизм имеет потенциальные уязвимости ввиду необходимости использовать криптостойкий генератор случайных чисел для формирования случайного сеансового ключа симметричного шифрования и эффективно противостоящий атакам симметричный криптоалгоритм (в данное время широкое применение находят AES, Serpent,
Примечания
- ↑ U.S. Patent 4405829 (англ.)
Ссылки
Литература
- A. Menezes, P. van Oorschot, S. Vanstone. Handbook of Applied Cryptography. — CRC-Press, 1996. — 816 p. — (Discrete Mathematics and Its Applications). — ISBN 0-8493-8523-7
- Венбо Мао. Современная криптография: теория и практика = Modern Cryptography: Theory and Practice. — М.: «Вильямс», 2005. — 768 с. — ISBN 0-13-066943-1
- Нильс Фергюсон, Брюс Шнайер. Практическая криптография = Practical Cryptography: Designing and Implementing Secure Cryptographic Systems. — М.: «Диалектика», 2004. — 432 с. — ISBN 0-471-22357-3
- Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — 816 с. — 3000 экз. — ISBN 5-89392-055-4
- Если
Wikimedia Foundation. 2010.

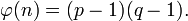
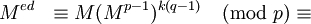
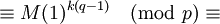

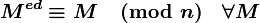
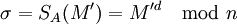
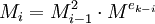

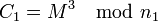
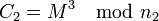

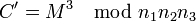
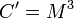
![g_1(x)=f(x)^e-C_1 \in \mathbb{Z}_n[x] \,](/pictures/wiki/files/56/8b85857367b2680f1602a847bd80c53b.png)