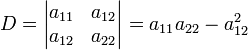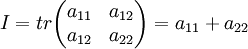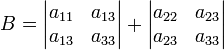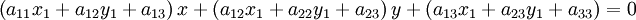- Кривые второго порядка
-
Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
- a11x2 + a22y2 + 2a12xy + 2a13x + 2a23y + a33 = 0,
в котором по крайней мере один из коэффициентов
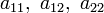 отличен от нуля.
отличен от нуля.История
Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и провращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же сечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур (см. ниже).
Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Еще позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижению второй космической скорости тело по параболе покинет поле притяжения Земли.
Инварианты
Вид кривой зависит от четырёх инвариантов:
- инварианты относительно поворота и сдвига системы координат:
- инвариант относительно поворота системы координат (полуинвариант):
Характеристическая квадратичная форма и характеристическое уравнение
Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой
F0(x,y) = a11x2 + 2a12xy + a22y2.
Так, например, невырожденная кривая (
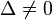 ) оказывается действительным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости от того, будет ли F0(x,y) положительно определённой, отрицательно определённой, неопределённой или полуопределённой квадратичной формой, что устанавливается по корням характеристического уравнения:
) оказывается действительным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости от того, будет ли F0(x,y) положительно определённой, отрицательно определённой, неопределённой или полуопределённой квадратичной формой, что устанавливается по корням характеристического уравнения: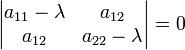
или
λ2 − Δλ + D = 0.
Корни этого уравнения являются собственными значениями действительной симметричной матрицы

и, как следствие этого всегда действительны.
Классификация кривых второго порядка
Невырожденные кривые
Кривая второго порядка называется невырожденной, если
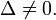 Могут возникать следующие варианты:
Могут возникать следующие варианты:- Невырожденная кривая второго порядка называется центральной если
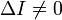
- эллипс — при условии D > 0 и ΔI < 0;
- частный случай эллипса — окружность — при условии I2 = 4D или a11 = a22,a12 = 0;
- мнимый эллипс (ни одной действительной точки) — при условии ΔI > 0;
- гипербола — при условии D < 0;
- эллипс — при условии D > 0 и ΔI < 0;
- Невырожденная кривая второго порядка называется нецентральной если ΔI = 0
- парабола — при условии D = 0.
Вырожденные кривые
Кривая второго порядка называется вырожденной, если Δ = 0. Могут возникать следующие варианты:
- действительная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии D > 0;
- пара действительная пересекающихся прямых (вырожденная гипербола) — при условии D < 0;
- вырожденная парабола — при условии D = 0:
- пара действительных параллельных прямых — при условии B < 0;
- одна действительная прямая (две слившиеся параллельные прямые) — при условии B = 0;
- пара мнимых параллельных прямых (ни одной действительной точки) — при условии B > 0.
Диаметры и центр кривой второго порядка
Диаметром кривой второго порядка называется геометрическое место середин параллельных хорд этой кривой. Полученный таким образом диаметр называется сопряжённым этим хордам или их направлению. Диаметр, сопряжённый хордам, образующих угол θ с положительным направлением оси Ox, определяется уравнением:
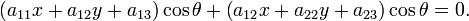
Если выпоняется условие
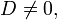 то все диаметры кривой пересекаются в одной точке — центре, а сама кривая называется центральной. В противном случае (D = 0) все диаметры кривой либо парралельны, либо совпадают.
то все диаметры кривой пересекаются в одной точке — центре, а сама кривая называется центральной. В противном случае (D = 0) все диаметры кривой либо парралельны, либо совпадают.Координаты центра
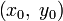 определяются системой уравнений:
определяются системой уравнений: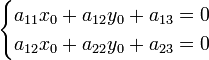
Решая эту систему относительно x0 и y0, получим:
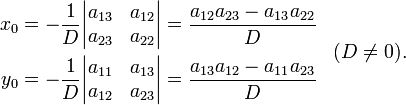
Если кривая центральная, то перенос начала координат в её центр приводит уравнение к виду
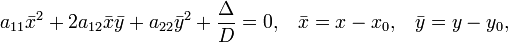
где
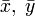 — координаты относительно новой системы.
— координаты относительно новой системы.Главные оси и вершины кривой второго порядка
Главной осью кривой второго порядка называется её диаметр, перпендикулярный к сопряжённым к ним хордам. Этот диаметр является осью симметрии кривой. Каждая центральная кривая
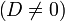 либо имеет две взаимно перпендикулярные оси, либо все диаметры являются главными осями. В последнем случае кривая является окружностью. Нецентральные кривые
либо имеет две взаимно перпендикулярные оси, либо все диаметры являются главными осями. В последнем случае кривая является окружностью. Нецентральные кривые 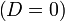 имеют лишь одну главную ось. Точки пересечения главной оси с самой кривой называются её вершинами.
имеют лишь одну главную ось. Точки пересечения главной оси с самой кривой называются её вершинами.Направляющие косинусы нормалей к главным осям удовлетворяют уравнениям

где λ — отличный от нуля корень характеристического уравнения. Направления главных осей и сопряжённых им хорд называются главными направлениями кривой. Угол между положительным направлением оси Ox и каждым из двух главных направлений определяется формулой
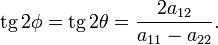
Из всех видов кривых второго порядка только окружность имеет неопределённые главные направления.
Уравнения
Общее уравнение в матричном виде
Общее уравнение кривой можно записать в матричном виде
Канонический вид
Вводом новой системы координат можно привести уравнения кривых второго порядка к стандартному каноническому виду (см. таблицу). Параметры канонических уравнений весьма просто выражаются через инварианты
 и корни характеристического уравнения
и корни характеристического уравнения 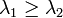 (см. выше раздел «Характеристическая квадратичная форма и характеристическое уравнение»).
(см. выше раздел «Характеристическая квадратичная форма и характеристическое уравнение»).Вид кривой Каноническое уравнение Инварианты Невырожденные кривые ( 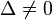 )
)Эллипс 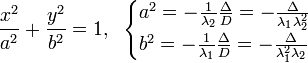
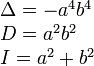
Гипербола 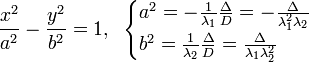
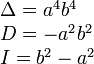
Парабола 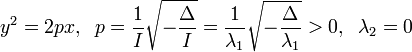
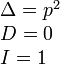
Вырожденные кривые (Δ = 0) Точка 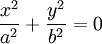

Две пересекающиеся прямые 
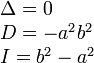
Две параллельные прямые 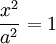
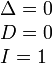
Одна прямая x2 = 0 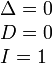
Для центральной кривой в каноническом виде её центр
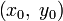 находится в начале координат.
находится в начале координат.Через эксцентриситет
Каноническое уравнение любой невырожденной кривой второго порядка при помощи подходящего преобразования начала координат может быть приведено к виду
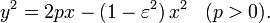
В этом случае кривая проходит через начало новой системы координат, а ось Ox является осью симметрии кривой. Данное уравнение выражает тот факт, что невырожденная кривая второго порядка является геометрическим местом точек, отношение расстояний которых
 (эксцентриситет) от данной точки (фокуса) и от данной прямой (директрисы) постоянно. Кроме того, при
(эксцентриситет) от данной точки (фокуса) и от данной прямой (директрисы) постоянно. Кроме того, при 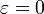 кривая является окружностью, при
кривая является окружностью, при 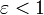 — эллипсом, при
— эллипсом, при 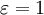 — параболой, при
— параболой, при  — гиперболой.
— гиперболой.Уравнение директриссы кривой выражается уравнением
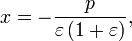 а координаты фокуса
а координаты фокуса 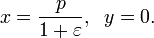 Директрисса перпендикулярна оси симметрии, проходящей через фокус и вершину кривой (фокальная ось). Расстояние между фокусом и директриссой равно
Директрисса перпендикулярна оси симметрии, проходящей через фокус и вершину кривой (фокальная ось). Расстояние между фокусом и директриссой равно 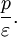
Если кривая второго порядка центральная (эллипс или гипербола), то прямая
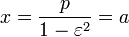
является осью симметрии и, следовательно, кривая имеет два фокуса и две директриссы.
Параметр p называется фокальным параметром и равен половине длины хорды, проходящей через фокус и перпендикулярной к фокальной оси (фокальная хорда).
Полярные координаты
Если взять в качестве полюса полярной системы координат
 фокус невырожденной кривой второго порядка, а в качестве полярной оси — её ось симетрии, то в полярных координатах ρ, φ уравнение кривой будет иметь вид
фокус невырожденной кривой второго порядка, а в качестве полярной оси — её ось симетрии, то в полярных координатах ρ, φ уравнение кривой будет иметь вид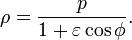
Кривая, заданная своими пятью точками
Кривая второго порядка вполне определяется пятью своими точками, если никакие четыре из них не лежат на одной прямой. Уравнение кривой, проходящей через точки
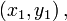
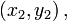
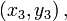
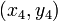 и
и 
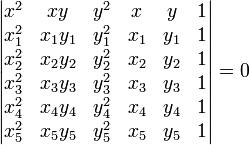
Кривая, заданная пятью точками вырождается в том и только в том случае, когда три из заданных точек лежат на одной прямой.
Касательные и нормали
Уравнение касательной к кривой второго порядка f(x,y) в её точке
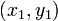 имеет вид:
имеет вид: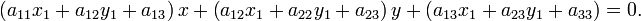
Уравнение нормали к кривой второго порядка в точке
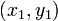 имеет вид
имеет вид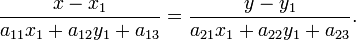
Полюсы и поляры
Уравнение
помимо касательной опряделяет прямую, называемую полярой точки
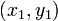 относительно кривой второго порядка, независимо от того, лежит ли эта точка на кривой или нет. При этом точка
относительно кривой второго порядка, независимо от того, лежит ли эта точка на кривой или нет. При этом точка 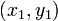 называется полюсом этой прямой. Поляра точки кривой есть её касательная в этой точке.
называется полюсом этой прямой. Поляра точки кривой есть её касательная в этой точке.Теоремы о полюсах и полярах:
- Если прямая, проведённая через полюс P, пересекает поляру в точке Q, а кривую второго порядка — в точках R1 и R2, то точки P и Q гармонически разделяют отрезок R1R2, т. е. выполняется условие
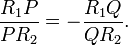
- Если точка лежит на некоторой прямой, то её поляра проходит через полюс этой прямой. Если прямая проходит через некоторую точку, то её полюс лежит на поляре этой точки.
- Диаметр кривой второго порядка есть поляра бесконечно удалённой точки, через которую проходят сопряжённые ему хорды, а центр кривой есть полюс бесконечно удалённой прямой.
- Фокус кривой есть центр пучка, обладающего тем свойством, что полюс любой его прямой принадлежит перпендикулярной к ней прямой пучка. Директрисса есть поляра фокуса.
Из этих утверждений, в частности, следует, что:
- если через точку можно провести две касательные к кривой, то то поляра этой точки проходит через точки касания;
- касательные к кривой в концах диаметра параллельны сопряжённым ему хордам;
- точка пересечения касательных к кривой в концах любой её хорды, проходящей через фокус, лежит на директриссе;
- каждая хорда, проходящая через фокус, перпендикулярна к прямой, проведённой через её фокус и точку пересечения касательных в концах хорды.
Теоремы, связанные с кривыми второго порядка
- Теорема Паскаля: точки пересечения противоположных сторон шестиугольника, вписанного в кривую второго порядка, лежат на одной прямой.
- Теорема Брианшона: диагонали, проходящие через противоположные вершины шестиугольника, описанного около кривой второго порядка, пересекаются в одной точке.
См. также
Ссылки
Литература
- Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64-69.
Wikimedia Foundation. 2010.