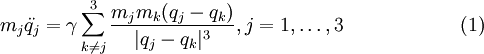Задача трех тел

Задача трёх тел (в астрономии) — частная задача небесной механики, состоящая в определении относительного движения трёх тел (материальных точек), взаимодействующих по закону тяготения Ньютона (например, Солнца, Земли и Луны). В общем случае не существует решения этой задачи. Известно только 5 точных решений для специальных начальных скоростей и координат объектов.

Математическая формулировка

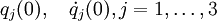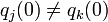Общая задача 3-тел в небесной механике является задачей с начальными условиями для системы обыкновенных дифференциальных уравнений. Для заданных начальных условий $q_j(0), \quad\dot q_j(0), j=1,\ldots,3$ и $q_j(0) \neq q_k(0)$ для различных j и k , нужно найти решение системы уравнений второго порядка

$m_j \ddot{q_j} = \gamma \sum\limits_{k\neq j }^{3} \frac{m_j m_k({q_j}-{q_k})}{|q_j-q_k|^3}, j=1,\ldots,3 \qquad \qquad \qquad (1)$

где m₁,m₂,m₃ — массы тел, и q₁,q₂,q₃ — их трёхмерные векторные функции, зависящие от времени t, описывающие положение этих масс.

Частные решения

Во всех пяти известных на данный момент точных решениях отношения расстояний между телами остаются неизменными.

Первые три решения были найдены Эйлером. Они имеют место, когда все три тела находятся на одной прямой. В этом случае имеют место 3 возможных последовательности расположения (третье тело находится между двумя другими, либо слева или справа от обоих). Такое движение называется коллинеарным.

Ещё два решения нашел в 1772 году Лагранж. В них треугольник, образованный телами, сохраняется равносторонним, вращаясь в пространстве либо по часовой стрелке, либо против часовой стрелки.

Общий случай

Относительно общего случая Вейерштрасс предложил такую задачу (1885 г., конкурс на премию шведского короля Оскара II):

Пусть дана система произвольного числа материальных точек, взаимодействующих по закону Ньютона. Требуется, в предположении, что не произойдет соударения каких либо двух точек, представить координаты каждой точки в виде рядов по каким либо непрерывным функциям времени, равномерно сходящихся для всех действительных значений этой переменной.^[1]

По всей видимости, сам Вейерштрасс, опираясь на свою знаменитую теорему об аппроксимации произвольной функции полиномами, желал получить выражение для координат тел в виде

$\lim \limits_{n\rightarrow \infty}P_{n}(t)$,

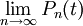где P_n — некоторые полиномы. Существование таких полиномов сразу следует из непрерывности решения, но найти конструктивный способ отыскания полиномов до сих пор не удалось.

Обсуждение самой возможности ситуации, описанной в задаче Вейерштрасса, привело к ряду важных выводов:

• Если решение задачи трех тел является голоморфной функцией t в интервале [0,t₀) и перестает быть таковым при t = t₀, то при 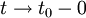$t\rightarrow t_0-0$ или все расстояния между телами стремятся к нулю (тройное соударение тел), или одно из них стремится к нулю, а остальные два — к конечным пределам (простое соударение тел). (Пенлеве, 1897)
• Тройное соударение в задаче трех тел возможно лишь при условии обращения в нуль момента импульса системы и, следовательно, может иметь место лишь при весьма специальных начальных данных. (Ф. А. Слудский, 1874)
• Если момент импульса системы не равен нулю, то существует т. н. регуляризирующий параметр s, через который можно выразить координаты и время голоморфным образом в окрестности вещественной оси s. (Зундман, 1912; короткое доказательство дал в 1967 Бурде (Burdet)^[2])

Это подтолкнуло Пуанкаре и Зундмана искать решение не в виде функций от t, а в виде рядов от некоторого параметра. Именно, координаты трех тел и время являются голоморфными функциями s вдоль всей вещественной оси плоскости s, то есть существует некоторая область, в которой координаты голоморфны. По теореме Римана эту область можно отобразить на круг единичного радиуса | v | < 1, поэтому координаты трех тел и время можно представить в виде функций параметра v, голоморфных в круге единичного радиуса. Такие функции представимы в виде сходящегося во всем круге рядов по положительным степеням v. Эти ряды были найдены Зундманом в 1912, точнее говоря, был найден алгоритм отыскания их коэффициентов. К несчастью, как показал Д. Белорицкий^[3], по крайней мере в случае Лагранжа для нужд вычислительной астрономии в сходящихся рядах Зудмана нужно брать как минимум 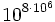$10^{8 \cdot 10^6}$ членов.

Литература

• Алексеев В. М. Лекции по небесной механике. Ижевск, 1999.
• Зигель К. Лекции по небесной механике.
• Маршал К. Задача трех тел. М.-Ижевск, 2004

Ссылки

1. ↑ Погребысский И. Б. Комм. к Задаче трех тел Пуанкаре// Пуанкаре А. Избранные труды. Т. 2. М.: Наука, 1979. С.967-976.
2. ↑ Маршал К. Задача трех тел. М.-Ижевск, 2004
3. ↑ Belorizky, D. Sur la solution du problème des trois corps, donnée par M. Sundman // C. R. 193, 766—768. Published: 1931

См. также

• Задача двух тел
• Гравитационная задача N тел