- Евклида алгоритм
-
Алгори́тм Евкли́да — алгоритм для нахождения наибольшего общего делителя двух целых чисел или наибольшей общей меры двух однородных величин.
Содержание
История
Древнегреческие математики называли этот алгоритм ἀνθυφαίρεσις или ἀνταναίρεσις — «взаимное вычитание». Этот алгоритм не был открыт Евклидом, так как упоминание о нём имеется уже в Топике Аристотеля. В «Началах» Евклида он описан дважды — в VII книге для нахождения наибольшего общего делителя двух натуральных чисел и в X книге для нахождения наибольшей общей меры двух однородных величин. В обоих случаях дано геометрическое описание алгоритма, для нахождения «общей меры» двух отрезков.
Историками математики (Цейтен и др.) было выдвинуто предположение, что именно с помощью алгоритма Евклида (процедуры последовательного взаимного вычитания) в древнегреческой математике впервые было открыто существование несоизмеримых величин (стороны и диагонали квадрата, или стороны и диагонали правильного пятиугольника). Впрочем, это предположение не имеет достаточных документальных подтверждений. Алгоритм для поиска наибольшего общего делителя двух натуральных чисел описан также в I книге древнекитайского трактата Математика в девяти книгах.
Ряд математиков средневекового Востока (Сабит ибн Курра, ал-Махани, Ибн ал-Хайсам, Омар Хайям) попытались построить на основе алгоритма Евклида теорию отношений, альтернативную по отношению теории отношений Евдокса, изложенной в V книге «Начал» Евклида. Согласно определению, предложенному этими авторами, четыре величины, первая ко второй и третья к четвёртой, имеют между собой одно и то же отношение, если при последовательном взаимном вычитании второй величин в обеих парах на каждом шаге будут получаться одни и те же неполные частные.
Алгоритм Евклида для целых чисел
Пусть a и b целые числа, не равные одновременно нулю, и последовательность чисел
определена тем, что каждое rk это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
- a = bq0 + r1
- b = r1q1 + r2
- r1 = r2q2 + r3
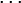
- rk − 2 = rk − 1qk − 1 + rk
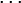
- rn − 1 = rnqn
Тогда НОД(a,b), наибольший общий делитель a и b, равен rn, последнему ненулевому члену этой последовательности.
Существование таких r1,r2,..., то есть возможность деления с остатком m на n для любого целого m и целого
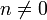 , доказывается индукцией по m.
, доказывается индукцией по m.Корректность этого алгоритма вытекает из следующих двух утверждений:
- Пусть a = bq + r, тогда gcd(a,b) = gcd(b,r).
- gcd(0,r) = r для любого ненулевого r.
Проще сформулировать алгоритм Евклида так: если даны натуральные числа a и b и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.
На С
// фукнция получения НОД int NOD(int a, int b) { // пока числа не равны 0 while(a!=0 && b!=0) { if(a>=b) a=a%b; else b=b%a; } return a+b; // Одно - ноль }
взято с [1]
Расширенный алгоритм Евклида и соотношение Безу
Формулы для ri могут быть переписаны следующим образом:
- r1 = a + b( - q0)
- r2 = b − r1q1 = a( − q1) + b(1 + q1q0)
- gcd(a,b) = rn = as + bt
здесь s и t целые. Это представление наибольшего общего делителя называется соотношением Безу, а числа s и t — коэффициентами Безу. Соотношение Безу является ключевым в доказательстве леммы Евклида и основной теоремы арифметики.
Связь с цепными дробями
Отношение a / b допускает представление в виде цепной дроби:
-
![\frac ab=[q_0; q_1, q_2,\cdots,q_n]](/pictures/wiki/files/54/60b453ad7c91fd519201831d804953f8.png) .
.
При этом цепная дробь без последнего члена равна отношению коэффициентов Безу t / s, взятому со знаком минус:
-
![[q_0; q_1, q_2,\cdots,q_{n-1}] = -\frac ts](/pictures/wiki/files/50/2f2b1e116a8094901e95149ea1ec66d0.png) .
.
Вариации и обобщения
- Кольца в которых применим алгоритм Евклида, называются евклидовыми кольцами, к ним относятся в частности кольцо многочленов.
Ускоренные версии алгоритма
- Одним из методов ускорения целочисленного алгоритма Евклида является использования симметричного остатка:
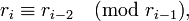
- где
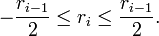
- Одна из наиболее многообещающих версий ускоренного алгоритма Евклида для полиномов основывается на том, что промежуточные значения алгоритма в основном зависят от высоких степеней. При применении стратегии Divide & Conqurer наблюдается большое ускорение асимптотической скорости алгоритма.
См. также
- Евклидово кольцо
- Непрерывная дробь
- Примеры реализации алгоритма Евклида
- Обоснование Алгоритма Евклида
Литература
- Виноградов И. М. Основы теории чисел.
- Курант Р., Роббинс Г. Что такое математика? Дополнение к главе I, § 4.
- Щетников А. И. Алгоритм Евклида и непрерывные дроби. Новосибирск: АНТ, 2003.
- Fowler D. H. The Mathematics of Plato’s Academy: a new reconstruction. 2nd ed. Oxford: Clarendon Press, 1999.
- von zur Gathen J., Gerhard J. Modern Computer Algebra. ISBN 0-521-82646-2
Wikimedia Foundation. 2010.