- Грина функция
-
Функция Грина - используется для решения неоднородных дифференциальных уравнений с граничными условиями (неоднородная краевая задача).
Функция Грина линейного оператора L, действующего на обобщённые функции над многообразием (в частности, над евклидовым пространством, в том числе над числовой прямой), определяется для точки x0 как решение уравнения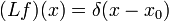 ,
,
где δ — дельта-функция Дирака, а x0 предполагается не входящим больше никуда, кроме разности в аргументе дельта-функции.
Если ядро оператора L нетривиально, тогда функция Грина не единственна. Однако на практике симметрии, граничные условия и дополнительные критерии позволяют выделить единственную функцию Грина. Cледует помнить, что вообще говоря функция Грина — не обычная, а обобщённая функция, то есть, иными словами, в некоторых случаях она может выпадать из класса обычных функций, например, иметь особенности вида дельта-функции или ее производных.
Функцию Грина можно представить как обратный оператор к L. Поэтому ее нередко символически обозначают как L − 1.
Функции Грина полезны в электростатике — для решения уравнения Пуассона; в теории конденсированных сред — где они позволяют разрешить уравнение диффузии (и совпадающее с ним уравнение теплопроводности); в квантовой механике — где функция Грина гамильтониана является одной из ключевых концепций и имеет отношение к плотности состояний. Функции Грина, используемые в этих областях, очень похожи, поскольку математическая структура уравнения диффузии и уравнения Шрёдингера подобны. Все области матфизики и теорфизики, где крайне полезны функции Грина, пожалуй трудно даже перечислить. Они помогают находить стационарные и нестационарные решения, в том числе при разнообразных граничных условиях, и т.д.В физике элементарных частиц функции Грина используются как пропагаторы в диаграммах Фейнмана (и выражение «функция Грина» часто применяется вообще к корреляционной функции в квантовой теории поля). Функция Грина широко применяется в приложениях теории рассеяния к физике твёрдого тела (рентгенография, расчёты электронных спектров металлических материалов).
Функция Грина названа в честь английского математика Джорджа Грина (англ. George Green), который первым развил соответствующую теорию в 1830-х гг.
Содержание
Основание
Свёртка с функцией Грина даёт решение неоднородного линейного интегро-дифференциального уравнения.
Пусть
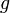 — функция Грина линейного оператора
— функция Грина линейного оператора 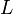 , тогда решение
, тогда решение 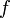 неоднородного уравнения
неоднородного уравнения 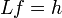 даётся интегралом:
даётся интегралом:- в одномерном случае, или
-в многомерном, где
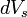 - элемент объема.
- элемент объема.Ключевым здесь можно считать разложение
 по базису из дельта-функций Дирака.
по базису из дельта-функций Дирака.Замечание
Иногда, когда неоднородное уравнение содержит в правой части постоянный коэффициент, то есть имеет вид
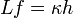 , функция Грина
, функция Грина 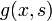 также определяется с учетом этого коэффициента, то есть, по определению тогда она есть решение уравнения
также определяется с учетом этого коэффициента, то есть, по определению тогда она есть решение уравнения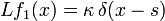 .
.
В этом случае решение исходного неоднородного уравнения
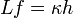 с произвольной функцией
с произвольной функцией 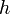 в правой части записывается как
в правой части записывается как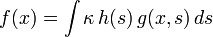 .
.
(Ясно, что описанное в этом параграфе отличие в определении функции Грина от данного в статье выше, касается не сути дела, а всего лишь предпочитаемой формы записи).
Функция Грина оператора Штурма — Лиувилля (одномерный случай)
Постановка задачи
Пусть
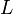 — оператор Штурма — Лиувилля, линейный дифференциальный оператор вида
— оператор Штурма — Лиувилля, линейный дифференциальный оператор видаи пусть
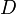 — оператор краевых условий
— оператор краевых условийПусть
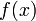 — непрерывная функция на промежутке
— непрерывная функция на промежутке ![[0,\;l]](/pictures/wiki/files/49/1e126249557db1326bb68ec9167f4ab6.png) . Предположим также, что задача
. Предположим также, что задачарегулярна, то есть существует только тривиальное решение однородной задачи.
Теорема Грина
Тогда существует единственное решение
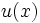 , удовлетворяющее системе
, удовлетворяющее системекоторое задаётся выражением
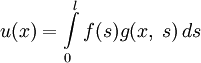 ,
,
где
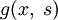 — функция Грина, которая удовлетворяет следующим требованиям:
— функция Грина, которая удовлетворяет следующим требованиям: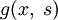 непрерывна по
непрерывна по 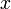 и
и  .
.- Для
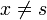 ,
, 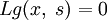 .
. - Для
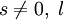 ,
, 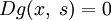 .
. - Скачок производной:
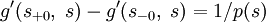 .
. - Симметрична:
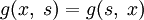 .
.
Пример
-См. ниже.
Нахождение функции Грина
В виде ряда через собственные функции оператора
Если множество собственных векторов (собственных функций)
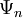 дифференциального оператора
дифференциального оператора 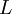
(то есть набор функций
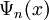 , таких, что для каждой найдется число
, таких, что для каждой найдется число 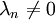 , что
, что 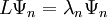 )
)полно, тогда мы можем построить функцию Грина из собственных векторов
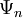 и собственных значений
и собственных значений 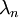 .
.Под полнотой подразумевается выполнение соотношения полноты для набора
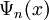 :
: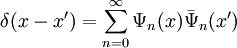 .
.
Можно показать, что
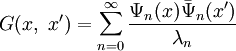 .
.
Действительно, подействовав оператором
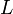 на эту сумму, мы получим дельта-функцию (в силу соотношения полноты).
на эту сумму, мы получим дельта-функцию (в силу соотношения полноты).(Чертой сверху обозначено комплексное сопряжение, если
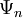 - вещественные функции, его можно не делать).
- вещественные функции, его можно не делать).Функция Грина для лапласиана
Функция Грина для лапласиана может быть readily put to use using the second of Green's identities.
To derive Green's theorem, begin with the divergence theorem (otherwise known as Gauss' law):
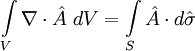 .
.
Let
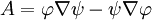 and substitute into Gauss' law. Compute
and substitute into Gauss' law. Compute 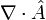 and apply the chain rule for the
and apply the chain rule for the  operator:
operator: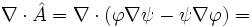
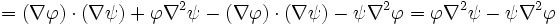 .
.
Plugging this into the divergence theorem, мы получаем Теорему Грина:
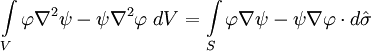 .
.
Suppose that our linear differential operator L is the Laplacian,
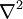 , and that we have a Green's function G for the Laplacian. The defining property of the Green's function still holds:
, and that we have a Green's function G for the Laplacian. The defining property of the Green's function still holds: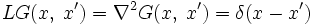 .
.
Let ψ = G in Green's theorem. We get:
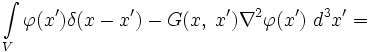
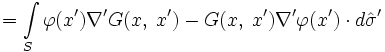 .
.
Используя выражение, мы можем решить уравнение Лапласа (
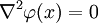 ) и уравнение Пуасона ((
) и уравнение Пуасона ((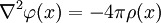 ) с граничными условиями Неймана или Дирихле. Другими словами, we can solve for
) с граничными условиями Неймана или Дирихле. Другими словами, we can solve for  everywhere inside a volume where either (1) the value of
everywhere inside a volume where either (1) the value of  is specified on the bounding surface of the volume (Dirichlet boundary conditions), or (2) the normal derivative of
is specified on the bounding surface of the volume (Dirichlet boundary conditions), or (2) the normal derivative of 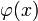 is specified on the bounding surface.
is specified on the bounding surface.Suppose we're interested in solving for
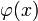 inside the region. Then the integral
inside the region. Then the integral 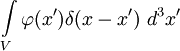 reduces to simply
reduces to simply 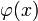 due to the defining property of the Dirac delta-function and we have:
due to the defining property of the Dirac delta-function and we have: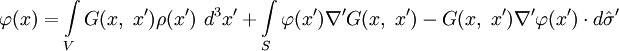 .
.
This form expresses the well-known property of harmonic functions, that if the value or normal derivative is known on a bounding surface, then the value of the function inside the volume is known everywhere.
In electrostatics, we interpret
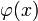 as the electric potential, ρ(x) as electric charge density, and the normal derivative
as the electric potential, ρ(x) as electric charge density, and the normal derivative 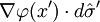 as the normal component of the electric field.
as the normal component of the electric field.If we're interested in solving a Dirichlet boundary value problem, we choose our Green's function such that
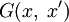 vanishes when either x or
vanishes when either x or 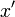 is on the bounding surface; conversely, if we're interested in solving a Neumann boundary value problem, we choose our Green's function such that its normal derivative vanishes on the bounding surface. Thus we are left with only one of the two terms in the surface integral.
is on the bounding surface; conversely, if we're interested in solving a Neumann boundary value problem, we choose our Green's function such that its normal derivative vanishes on the bounding surface. Thus we are left with only one of the two terms in the surface integral.With no boundary conditions, the Green's function for the Laplacian is:
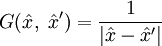 .
.
Supposing that our bounding surface goes out to infinity, and plugging in this expression for the Green's function, we arrive at the familiar expression for electric potential in terms of electric charge density:
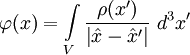 .
.
Пример
(Этот пример служит иллюстрацией к параграфу Функция Грина оператора Штурма — Лиувилля (одномерный случай), причем описанные здесь соображения иллюстрируют пункты теоремы из соответствующего параграфа, ссылки на пункты которой присутствуют в тексте ниже).
Дана задача
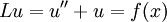 ;
;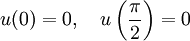 .
.
Найти функцию Грина.
Первый шаг: Функция Грина
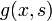 в данном случае по определению должна быть решением уравнения
в данном случае по определению должна быть решением уравнения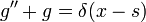 ,
,
где двумя штрихами обозначена вторая производная по x.
Для
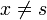 , где δ-функция равна нулю, это уравнение сводится к однородному (пункт 2 упомянутой теоремы):
, где δ-функция равна нулю, это уравнение сводится к однородному (пункт 2 упомянутой теоремы):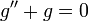 ,
,
то есть для всех точек, кроме s, функция Грина будет решением такого однородного уравнения.
Общее решение такого уравнения
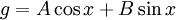 ,
,
где
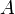 и
и 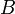 - константы (не зависят от
- константы (не зависят от 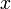 ).
).Таким образом,
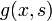 должно иметь именно такой вид всюду, кроме точки
должно иметь именно такой вид всюду, кроме точки  , причем слева и справа от нее коэффициенты
, причем слева и справа от нее коэффициенты 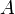 и
и 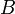 могут (и будут) иметь разное значение.
могут (и будут) иметь разное значение.Наложим на функцию Грина граничные условия, совпадающие с граничными условиями исходной задачи (пункт 3 упомянутой во вводном замечании теоремы). Функция Грина с наложенными так граничными условиями удобна тем, что конструируемые суммированием или интегрированием таких функций Грина решения автоматически будут удовлетворять этим граничным условиям.
Из левого граничного условия:
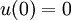 - налагаемого на функцию Грина мы видим, что для
- налагаемого на функцию Грина мы видим, что для 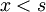 коэффициент
коэффициент 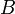 общего решения должен быть нулем, то есть для
общего решения должен быть нулем, то есть для 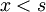
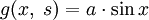 .
.
Точно так же из правого граничного условия:
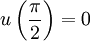 - получаем равенство нулю коэффициента
- получаем равенство нулю коэффициента 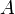 , то есть для
, то есть для 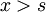
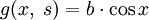 .
.
В итоге, учитывая, что коэффициенты a и b вообще говоря могут зависеть от s, можем записать:
Второй шаг:
Нужно определить
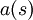 и
и 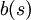 .
.Проинтегрировав дважды левую и правую часть уравнения с дельта-функцией в правой части, мы увидим, что функция Грина должна быть непрерывна (пункт 1 упомянутой теоремы), а отсюда условие сшивки решения x < s и x > s:
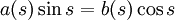 .
.
Проинтегрировав же левую и правую часть того же уравнения получим условие на скачок первой производной (пункт 4 теоремы), и используя его, получим:
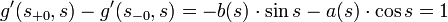 .
.Используя правило Крамера или просто угадывая решение системы из двух этих уравнений, получим, что
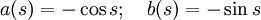 .
.Эти выражения удовлетворяют условию пункта 5 теоремы.
Тогда функция Грина задачи:
Другие примеры
- Пусть дано множество
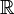 и оператор L равен d / dx. Тогда функция Хевисайда H(x − x0) является функцией Грина для L при x0.
и оператор L равен d / dx. Тогда функция Хевисайда H(x − x0) является функцией Грина для L при x0. - Пусть многообразие задаётся первой четвертью плоскости
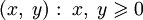 и L — оператор Лапласа. Также предположим, что при x = 0 наложены краевые условия Дирихле, при y = 0 — краевые условия Неймана. Тогда функция Грина примет вид
и L — оператор Лапласа. Также предположим, что при x = 0 наложены краевые условия Дирихле, при y = 0 — краевые условия Неймана. Тогда функция Грина примет вид
См. также
Литература
- Eyges, Leonard, The Classical Electromagnetic Field, Dover Publications, New York, 1972. ISBN 0-486-63947-9. (5-я глава содержит очень понятное изложение использования функций Грина для решения краевых задач в электростатике.)
- A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (2nd edition), Chapman & Hall/CRC Press, Boca Raton, 2003. ISBN 1-58488-297-2
- A. D. Polyanin, Handbook of Linear Partial Differential Equations for Engineers and Scientists, Chapman & Hall/CRC Press, Boca Raton, 2002. ISBN 1-58488-299-9
Wikimedia Foundation. 2010.

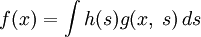
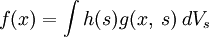
![L={d\over dx}\left[p(x){d\over dx}\right]+q(x)](/pictures/wiki/files/50/27c569c3fe145a50d74fab3caa8c311f.png)
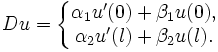
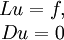
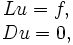
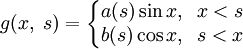
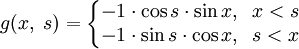
![G(x,\;y,\;x_0,\;y_0)=\frac{1}{2\pi}\left[\ln\sqrt{(x-x_0)^2+(y-y_0)^2}-\ln\sqrt{(x+x_0)^2+(y-y_0)^2}\right]+](/pictures/wiki/files/48/00311cf655335b8d46685cf72b71972b.png)
![+\frac{1}{2\pi}\left[\ln\sqrt{(x-x_0)^2+(y+y_0)^2}-\ln\sqrt{(x+x_0)^2+(y+y_0)^2}\right].](/pictures/wiki/files/49/1a6743e41c576ca387a97a856cf25711.png)