Π-теорема

π-теорема — основополагающая теорема анализа размерностей. Теорема утверждает, что если имеется физически значимое выражение, включающее в себя n физических переменных, и эти переменные описываются при помощи k независимых фундаментальных физических величин, то исходное выражение эквивалентно выражению, включающему множество из p = n — k безразмерных величин, построенных из исходных переменных. Это позволяет вычислять множество безразмерных величин по данным физическим значениям, даже если неизвестно выражение, связывающее эти значения. Способ выбора множества безразмерных параметров не единственный: π-теорема демонстрирует, как это можно сделать, но не обеспечивает, что полученные параметры будут наиболее «физически значимыми».

История

π-теорема, идеи которой были впервые методически изложены Н. А. Морозовым в монографии «Основы качественного физико-математического анализа и новые физические факторы, обнаруживаемые им в различных явлениях природы» (1908)., была опубликована Эдгаром Бакингемом (англ.) в 1917 году, а впоследствии и обобщена Германом Вейлем в 1926. Поэтому за рубежом она именуется «теорема Бакингема» (см. интервики), либо «теорема Ваши-Бакингема».

Теорема

Если дано физически значимое выражение:

$f ( q_1, q_2, \ldots , q_n ) = 0$,

где q_i — это n различных физических переменных и они выражаются через k независимых физических величин, то это выражение может быть переписано в виде:

$F ( {\pi}_1, {\pi}_2, \ldots , {\pi}_p ) = 0$,

где π_i — это безразмерные параметры, полученные из q_i при помощи p = n — k выражений следующего вида:

${\pi}_i = {q_1}^{m_1} \cdot {q_2}^{m_2} \cdot \ldots \cdot {q_n}^{m_n}$,

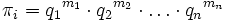где показатели степеней m_i — это рациональные числа.

Доказательство

Дана система из n разменных величин (физических величин) в k (физических) измерениях. Запишем матрицу M. Её строками будут измерения, а столбцами — физические величины: элемент (i, j) этой матрицы соответствует степени i-го множителя в формуле размерности j-й физической величины. Матрица может быть проинтерпретирована следующим образом: столбцу

$\left[ \begin{array}{ccc} {m_1} \\ {m_2} \\ \vdots \\ {m_n} \end{array} \right]$

соответствует запись

${q_1}^{m_1} \cdot {q_2}^{m_2} \cdot \ldots \cdot {q_n}^{m_n}$

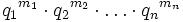
Очевидно, что безразмерным величинам соответствуют нулевые столбцы матрицы. Эти столбцы являются линейными комбинациями столбцов, соответствующих размерным величинам.

Как известно, любая система из n векторов в k-мерном линейном пространстве удовлетворяет системе из p = n — k отношений. И любой её базис будет состоять из p элементов, которым соответствуют безразмерные величины.

Безразмерные величины всегда могут быть выбраны таким образом, чтобы быть целочисленной комбинацией размерных величин. Это математический, иногда несамый лучший способ определения безразмерных величин. Некоторые способы выбора безразмерных величин более физически значимы (например, имеют смысл отношения характерных сил), и они должны использоваться в идеале.

См. также

• Анализ размерности
• Критерий подобия, безразмерные числа
• Размерность физической величины

Библиография

• Buckingham, E. (1914). «On physically similar systems; illustrations of the use of dimensional equations». Phys. Rev. 4: 345—376.