- Эйлерова характеристика
-
Эйлерова характеристика или характеристика Эйлера — Пуанкаре — характеристика топологического пространства. Эйлерова характеристика пространства
 обычно обозначается
обычно обозначается  .
.Содержание
Определения
- Для конечного клеточного комплекса (в частности для конечного симплициального комплекса) эйлерова характеристика может быть определена как знакопеременная сумма
- где
 обозначает число клеток размерности
обозначает число клеток размерности  .
.
- Эйлерова характеристика произвольного топологического пространства может быть определена через числа Бетти
 как знакопеременная сумма:
как знакопеременная сумма:
- Это определение имеет смысл только если все числа Бетти конечны и обнуляются для всех достаточно больших индексов.
- Последнее определение обобщает предыдущее и обобщается на другие гомологии с произвольными коэффициентами.
Свойства
- Эйлерова характеристика является гомотопическим инвариантом; то есть сохраняется при гомотопической эквивалентности топологических пространств.
- В частности, эйлерова характеристика есть топологический инвариант.
Эйлерова характеристика полиэдров
- Эйлерова характеристика двумерных топологических полиэдров может быть посчитана по формуле:
 где Г, Р и В суть числа граней, рёбер и вершин соответственно. В частности, для выпуклого многогранника верна формула Эйлера:
где Г, Р и В суть числа граней, рёбер и вершин соответственно. В частности, для выпуклого многогранника верна формула Эйлера:
- Например, Эйлерова характеристика для куба равна 6 − 12 + 8 = 2, а для треугольной пирамиды 4 − 6 + 4 = 2.
Теорема Гаусса — Бонне
Для компактного двумерного ориентированного риманова многообразия (поверхности)
 без границы существует формула Гаусса — Бонне, связывающая эйлерову характеристику
без границы существует формула Гаусса — Бонне, связывающая эйлерову характеристику  с гауссовой кривизной
с гауссовой кривизной  многообразия:
многообразия:где
 — элемент площади поверхности
— элемент площади поверхности  .
.- Существует обобщение формулы Гаусса-Бонне для двумерного многообразия с краем.
- Существует обобщение формулы Гаусса — Бонне на чётномерное римановых многообразий многообразия известная, как Теорема Гаусса — Бонне — Черна или Обобщённая формула Гаусса — Бонне.
- Существует также дискретный аналог теоремы Гаусса — Бонне, гласящий, что Эйлерова характеристика равна сумме дефектов полиэдра, делённой на
 .[1]
.[1]
- Существует комбинаторные аналоги формулы Гаусса — Бонне.
Ориентированные и неориентированные поверхности
- Эйлерова характеристика для ориентированной сферы с ручками выражается формулой:
 , где g - число ручек, для неориентированной поверхности формула выглядит, как
, где g - число ручек, для неориентированной поверхности формула выглядит, как  .
.
Величина эйлеровой характеристики
Название Вид Эйлерова характеристика Отрезок 
1 Окружность 
0 Круг 
1 сфера 
2 Тор
(произведение двух окружностей)
0 Двойной тор 
−2 Тройной тор 
−4 Проективная поверхность 
1 Лист Мёбиуса 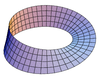
0 Бутылка Клейна 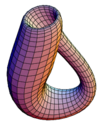
0 Две сферы(несвязные) 

2 + 2 = 4 Три сферы 


2 + 2 + 2 = 6 История
В 1752 году Эйлер[2] опубликовал формулу, связывающую между собой количество граней трёхмерного многогранника. В оригинальной работе формула приводится в виде
где S — количество вершин, H — количество граней, A — количество рёбер.
Ранее эта формула встречается в рукописях Р. Декарта, опубликованных в XVIII в.
В 1899 году Пуанкаре[3] обобщил эту формулу на случай N-мерного многогранника:
где
 — количество i-мерных граней N-мерного многогранника.
— количество i-мерных граней N-мерного многогранника.Если формально считать сам многогранник своей собственной единственной гранью размерности N, формулу можно записать в более простом виде:
Примечания
- ↑ Practical Polygonal Mesh Modeling with Discrete Gaussian-Bonnet Theorem
- ↑ L. Euler Demonstratio nonnullarum insignium proprietatum, quibus solida hedris planis inclusa sunt praedita. Novi Commentarii Academiae Scientiarum Petropolitanae 4:140–160, 1758. Представлено Санкт-Петербургской Академии 6 апреля 1752 года. Opera Omnia 1(26): 94–108.
- Перевод на английский язык: Leonhard Euler Proof of Some Notable Properties with wich Solids Enclosed by Plane Faces are Endowed. (Translated by Christopher Francese and David Richeson)
- ↑ H. Poincaré, Sur la généralisation d'un théorème d'Euler relatif aux polyèdres, Compt. Rend. Acad. Sci., 117 (1893), 144-145; Oeuvres, Vol. XI, 6-7.
Литература
- Долбилин Н. Три теоремы о выпуклых многогранниках // Квант. — 2001. — № 5. — С. 7-12.
- Лакатос И. Доказательства и опровержения. Как доказываются теоремы / Пер. И. Н. Веселовского. — М.: Наука, 1967.
- Шашкин Ю. А. Эйлерова характеристика. — М.: Наука, 1984. — Т. 58. — (Популярные лекции по математике).
См. также
Для улучшения этой статьи по математике желательно?: - Проставив сноски, внести более точные указания на источники.
Категория:- Алгебраическая топология
- Для конечного клеточного комплекса (в частности для конечного симплициального комплекса) эйлерова характеристика может быть определена как знакопеременная сумма
Wikimedia Foundation. 2010.







