Работа силы

Пусть материальная точка M движется по непрерывно дифференцируемой кривой G = {r = r(s)}, где s — переменная длинна дуги,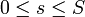$0\le s\le S$. Пусть на рассматриваемую материальную точку, находящуюся в положение r(s), действует сила F(s), направленная по касательной к траектории в направлении движения (точнее F(s) - численная величина этой силы).

Возьмем какое-либо разбиение 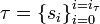$\tau = {\{ s_i \} }^{i=i_\tau} _{i=0}$ отрезка [0,S]. Ему соответствует разбиение траектории G на части

$G_i=\{ r(s), s_{i-1}\leq s \leq s_i\}, i=1,...,i_\tau$.

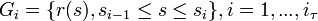Выберем произвольно по точке $\xi \leq [s_{i-1}, s_i]$ (см. рисунок)

Величина 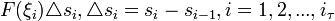$F(\xi _i)\triangle s_i, \triangle s_i = s_i - s_{i-1}, i=1,2,...,i_{\tau}$, называется элементарной работой силы F на участке G_i и принимается за приближенное значение работы, которую производит сила F, воздействующая на материальную точку, когда последняя проходит кривую G_i. Сумма всех элементарных работ 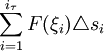$\sum_{i=1} ^{i_{\tau}}F(\xi_i)\triangle s_i$ является интегральной суммой Римана функции F(s).

Определение

Предел, к которому стремится сумма 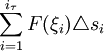$\sum_{i=1} ^{i_{\tau}}F(\xi_i)\triangle s_i$ всех элементарных работ, когда мелкость | τ | разбиения τ стремится к нулю, называется работой силы F вдоль кривой G.

Таким образом, если обозначить эту работу буквой W, то, в силу данного определения,

$W=\lim_{|\tau |\rightarrow 0} \sum_{i=1} ^{i_{\tau}}F(\xi_i)\triangle s_i$,

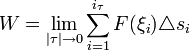следовательно,

1) $W=\int \limits_0 ^s F(s)ds$.

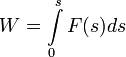Если положение точки на траектории ее движения описывается с помощью какого-либо другого параметра t (например, времени) и если величина пройденного пути s = s(t), 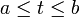$a\leq t \leq b$ является непрерывно дифференцируемой функцией, то из формулы 1) получим

$W=\int\limits_a ^b F[s(t)]s'(t)dt.$

Еще одно определение работы

Пусть на покоящееся тело начала действовать некоторая постоянная сила F. Под действием этой силы тело начнет движение и переместится на расстояние s, причем направление силы и перемещения совпадут. Вместе с телом будет двигаться и точка приложения силы.Эта точка также сдвинется на расстояние s Работа силы W = Fs в данном случае - произведение силы на перемещение точки приложения силы. Если же, несмотря на действие силы перемещения точки ее приложения не происходит,то W = 0. Например, если груз неподвижно висит на подвесе, то работа силы тяжести равна 0. Но при опускании или подъеме груза сила тяжести совершает работу W = F_Th, (h - расстояние на которое опустился или поднялся груз,F_T - сила тяжести).

Работа силы, перпендикулярной к перемещению

Если перемещение происходит в направлении, перпендикулярном к направлению силы, то сила не влияет на перемещение в этом направлении, поэтому считают, что работа силы равна 0. Например, при перемещении по горизонтальной плоскости работа силы тяжести равна 0

Работа силы тяжести равна 0

Работа силы, направленной под любым углом к перемещению

Для простоты считаем силу постоянной, а движение точки перемещения прямолинейным.

Угол между s и F > 90

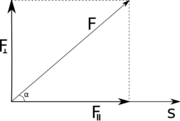Угол между s и F < 90

Разложим силу F на две составляющие: параллельную к перемещению и перпендикулярную к нему (см.рис). Исходя из вышесказанного, работу будет совершать только параллельная перемещению составляющая. Исходя из рисунка, эта проекция будет равна Fcosα, значит работа равна W = Fscosα. Из математики известно, что для двух векторов величина, равная произведению длин (модулей) двух векторов на косинус угла между ними называется скалярным произведением, значит работа 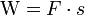$\mbox{W}=F\cdot s$, причем если α < 90 - работа положительна, больше - отрицательна. Но s = vt, Значит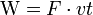 $\mbox{W}=F\cdot vt$

Литература

• Кудрявцев Л. Д. Курс математического анализа. — 5-е, переработанное и дополненное. — М.: Дрофа, 2003. — Т. 1. — С. 640—641. — 703 с.