- Минимизация логических функций методом Квайна
-
Метод Куайна — способ представления функции в ДНФ или КНФ с минимальным количеством членов и минимальным набором переменных.[1][2][3]
Преобразование функции можно разделить на два этапа:- на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемой сокращённой форме;
- на втором этапе — переход от сокращённой формы к минимальной форме.
Содержание
Первый этап (получение сокращённой формы)
Представим, что заданная функция
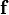 представлена в СДНФ. Для осуществления первого этапа преобразование проходит два действия:
представлена в СДНФ. Для осуществления первого этапа преобразование проходит два действия:- Операция склеивания;
- Операция поглощения.
Операция склеивания сводится к нахождению пар членов, соответствующих виду
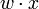 или
или 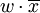 , и преобразованию их в следующие выражения:
, и преобразованию их в следующие выражения: 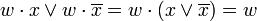 . Результаты склеивания w теперь играют роль дополнительных членов.
. Результаты склеивания w теперь играют роль дополнительных членов.Потом выполняется операция поглощения. Она основана на равенстве
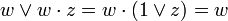 (член
(член 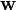 поглощает выражение
поглощает выражение 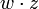 ). В следствие этого действия из логического выражения вычёркиваются все члены, поглощаемые другими переменными, результаты которых получены в операции склеивания.
). В следствие этого действия из логического выражения вычёркиваются все члены, поглощаемые другими переменными, результаты которых получены в операции склеивания.
Обе операции первого этапа могут выполнятся до тех пор, пока это может быть осуществимо.
Применение этих операций продемонстрировано в таблице: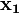
0 0 0 0 1 1 1 1 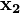
0 0 1 1 0 0 1 1 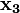
0 1 0 1 0 1 0 1 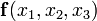
0 0 1 0 1 1 1 1 СДНФ выглядит так:
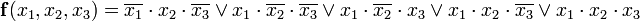
Результат операции склеивания нужен для преобразования функции на втором этапе (поглощения)
Членами результата склеивания являются
Член
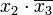 поглощает те члены исходного выражения, которые содержат
поглощает те члены исходного выражения, которые содержат 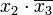 , то есть первый и четвёртый. Эти члены вычёркиваются. Член
, то есть первый и четвёртый. Эти члены вычёркиваются. Член 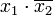 поглощает второй и третий, а член
поглощает второй и третий, а член 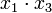 — пятый член исходного выражения.
— пятый член исходного выражения.Повторение обеих операций приводит к следующему выражению:
Здесь склеивается пара членов
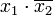 и
и 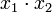 (склеивание пары членов
(склеивание пары членов 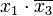 и
и 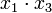 приводит к тому же результату), результат склеивания
приводит к тому же результату), результат склеивания 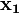 поглощает 2-, 3-, 4-, 5-й члены выражения. Дальнейшее проведение операций склеивания и поглощения оказывается невозможным, сокращённая форма выражения заданной функции (в данном случае она совпадает с минимальной формой)
поглощает 2-, 3-, 4-, 5-й члены выражения. Дальнейшее проведение операций склеивания и поглощения оказывается невозможным, сокращённая форма выражения заданной функции (в данном случае она совпадает с минимальной формой)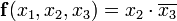
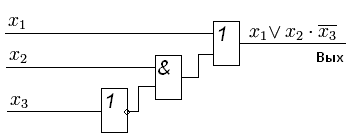
 Структурная схема функции
Структурная схема функцииЧлены сокращённой формы (в нашем случае это
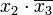 и
и 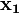 ) называются простыми импликантами функции. В итоге, мы получили наиболее простое выражение, если сравнивать его с начальной версией — СДНФ. Структурная схема такого элемента показана на рисунке справа.
) называются простыми импликантами функции. В итоге, мы получили наиболее простое выражение, если сравнивать его с начальной версией — СДНФ. Структурная схема такого элемента показана на рисунке справа.Второй этап (получение минимальной формы)
Как и на первом этапе, в полученном равенстве могут содержаться члены, устранение которых никаким образом не повлияет на конечный результат. Следующий этап минимизации — удаление таких переменных. Таблица, представленная ниже содержит значения истинности функции, по ней будет собрана следующая СДНФ.
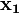
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 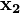
0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 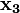
0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 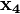
0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 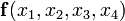
1 1 1 0 0 0 1 0 0 0 0 0 0 0 1 1 СДНФ, собранная по этой таблице выглядит следующим образом:
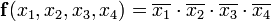
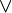
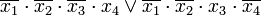
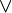
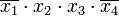
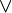
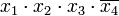
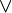
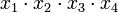
Конечное выражение достигается засчёт повторного использования операций склеивания и поглощения:
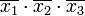
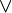
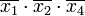
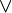
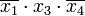
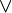
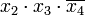
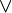
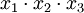
Члены этого выражения являются простыми импликантами выражения. Переход от сокращённой формы к минимальной осуществляется с помощью импликантной матрицы.
Члены СДНФ заданной функции вписываются в столбцы, а в строки — простые импликанты, то есть члены сокращённой формы. Отмечаются столбцы членов СДНФ, которые поглощаются отдельными простыми импликантами. В следующей таблице простая импликанта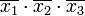 поглощает члены
поглощает члены 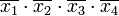 и
и 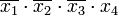 (в первом и во втором столбцах поставлены крестики).
(в первом и во втором столбцах поставлены крестики).Импликантная матрица
Простая импликанта 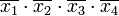
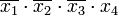
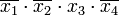
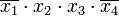
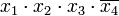
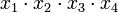
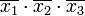
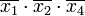
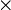
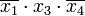
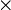
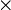
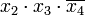
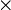
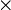
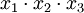
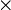
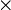
Вторая импликанта поглощает первый и третий члены СДНФ (указано крестиками) и т. д. Импликанты, не подлежащие исключению, образуют ядро. Такие импликанты определяются по вышеуказанной матрице. Для каждой из них имеется хотя бы один столбец, перекрываемый только этой импликантой.
В нашем примере ядро составляют импликанты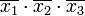 и
и 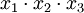 (ими перекрываются второй и шестой столбцы). Исключение из сокращённой формы одновременно всех импликант, не входящих в ядро, невозможно, так как исключение одной из импликант может превратить другую в уже нелишний член.
(ими перекрываются второй и шестой столбцы). Исключение из сокращённой формы одновременно всех импликант, не входящих в ядро, невозможно, так как исключение одной из импликант может превратить другую в уже нелишний член.
Для получения минимальной формы достаточно выбрать из импликантов, не входящих в ядро, такое минимальное их число с минимальным количеством букв в каждом из этих импликант, которое обеспечит перекрытие всех столбцов, не перекрытых членами ядра. В рассматриваемом примере необходимо импликантами, не входящими в ядро, перекрыть третий и четвёртый столбцы матрицы. Это может быть достигнуто различными способами, но так как необходимо выбирать минимальное число импликант, то, очевидно, для перекрытия этих столбцов следует выбрать имликанту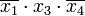 .
.
Минимальная дизъюнктивная нормальная форма (МДНФ) заданной функции:Нажмите на изображение для его увеличения 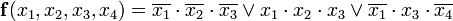 (а)
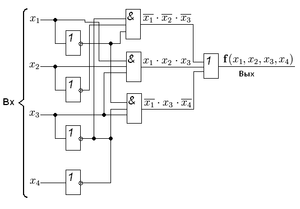
(а)Структурная схема, соответствующая этому выражению приведена на рисунке слева. Переход от сокращённой схемы к МДНФ был осуществлён путём исключения лишних членов — импликант
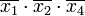 и
и 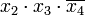 . Покажем допустимость подобного исключения членов из логического выражения.
. Покажем допустимость подобного исключения членов из логического выражения.
Импликанты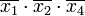 и
и 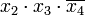 становятся равными лог. 1 соответственно при следующих наборах значений аргументов:
становятся равными лог. 1 соответственно при следующих наборах значений аргументов: 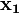 = 0,
= 0, 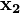 = 0,
= 0, 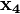 = 0 и
= 0 и 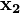 = 1,
= 1, 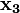 = 1,
= 1, 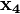 = 0.
= 0.
Роль этих импликант в выражении сокращённой формы функции заключается лишь в том, чтобы на приведённых наборах значений аргументов присваивать функции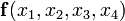 значение 1. Однако при этих наборах функция равна 1 из-за остальных импликант выражения. Действительно, подставляя набор значений, указанных выше в формулу (а), получаем:
значение 1. Однако при этих наборах функция равна 1 из-за остальных импликант выражения. Действительно, подставляя набор значений, указанных выше в формулу (а), получаем:- при
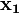 = 0,
= 0, 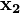 = 0,
= 0, 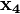 = 0
= 0
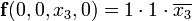
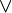
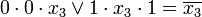
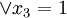 ;
;- при
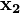 = 1,
= 1, 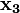 = 1,
= 1, 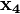 = 0
= 0
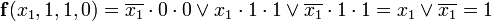 ;
;Использование метода для получения минимальной КНФ
Для получения Минимальной Конъюнктивной Нормальной Формы (МКНФ), используя метод Куайна, вводятся слудующие критерии:
- для минимизации берётся не СДНФ, а СКНФ функции;
- склеиваемые пары членов меняются на:
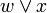 или
или 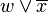 ;
; - правило операции поглощения выглядит следующим образом:
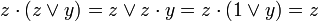
См. также
Примечания
- ↑ Краткое описание метода Куайна www.ptca.narod.ru
- ↑ Лекция: Минимизация ФАЛ www.works.tarefer.ru
- ↑ Пример минимизации переключательной функции методом Квайна www.matrixcalc.ru
Wikimedia Foundation. 2010.