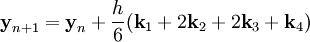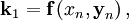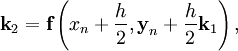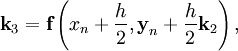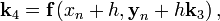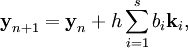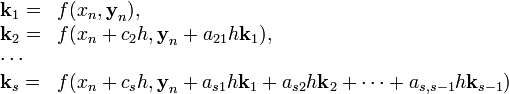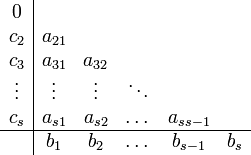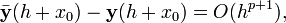Метод Рунге — Кутта

Метод Рунге — Кутта

Ме́тоды Ру́нге — Кутта́ (Ме́тоды Ру́нге — Кутты́) — важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

Формально, методом Рунге — Кутта является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения. Наиболее часто используется и реализована в различных математических пакетах (Maple, MathCAD, Maxima) стандартная схема четвёртого порядка. Иногда при выполнении расчётов с повышенной точностью применяются схемы пятого и шестого порядков^[1][2]. Построение схем более высокого порядка сопряжено с большими вычислительными трудностями^[3]. Методы седьмого порядка должны иметь по меньшей мере девять этапов, в схему восьмого порядка входит 11 этапов. Хотя схемы девятого порядка не имеют большой практической значимости, неизвестно, сколько этапов необходимо для достижения этого порядка. Аналогичная задача существует для схем десятого и более высоких порядков^[3].

Классический метод Рунге — Кутта 4 порядка

Метод Рунге—Кутта 4 порядка столь широко распространён, что его часто называют просто методом Рунге—Кутта.

Рассмотрим задачу Коши

$\textbf{y}'=\textbf{f}(x,\textbf{y}), \textbf{y}(x_0)=\textbf{y}_0.$.

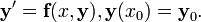Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:

$\textbf{y}_{n+1} = \textbf{y}_n + {h \over 6} (\textbf{k}_1 + 2\textbf{k}_2 + 2\textbf{k}_3 + \textbf{k}_4)$

где h — величина шага сетки по x и вычисление нового значения проходит в четыре этапа:

$\textbf{k}_1 = \textbf{f} \left( x_n, \textbf{y}_n \right),$

$\textbf{k}_2 = \textbf{f} \left( x_n + {h \over 2}, \textbf{y}_n + {h \over 2} \textbf{k}_1 \right),$

$\textbf{k}_3 = \textbf{f} \left( x_n + {h \over 2}, \textbf{y}_n + {h \over 2} \textbf{k}_2 \right),$

$\textbf{k}_4 = \textbf{f} \left( x_n + h, \textbf{y}_n + h \textbf{k}_3 \right),$

Этот метод имеет четвёртый порядок точности, т.е. суммарная ошибка на конечном интервале интегрирования имеет порядок O(h⁴) (ошибка на каждом шаге порядка O(h⁵)).

Прямые методы Рунге — Кутта

Семейство прямых методов Рунге — Кутта является обобщением метода Рунге — Кутта 4 порядка. Оно задаётся формулами

$\textbf{y}_{n+1} = \textbf{y}_n + h\sum_{i=1}^s b_i \textbf{k}_i,$

где h — величина шага сетки по x и вычисление нового значение проходит в s этапов:

$\begin{array}{ll} \textbf{k}_1 =& f(x_n, \textbf{y}_n),\\ \textbf{k}_2 =& f(x_n+c_2h, \textbf{y}_n+a_{21}h\textbf{k}_1),\\ \cdots&\\ \textbf{k}_s =& f(x_n+c_sh, \textbf{y}_n+a_{s1}h\textbf{k}_1+a_{s2}h\textbf{k}_2+\cdots+a_{s,s-1}h\textbf{k}_{s-1}) \end{array}$

Конкретный метод определяется числом s и коэффициентами b_i,a_ij и c_i. Эти коэффициенты часто упорядочивают в таблицу

$\begin{array}{c|ccccc} 0 &&&&&\\ c_2 & a_{21} &&&&\\ c_3 & a_{31} & a_{32} &&&\\ \vdots & \vdots & \vdots& \ddots&&\\ c_s & a_{s1} & a_{s2}& \dots & a_{ss-1}&\\ \hline & b_1 & b_2 & \dots & b_{s-1} & b_s \end{array}$

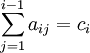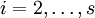Для коэффициентов метода Рунге — Кутта должны быть выполнены условия $\sum_{j=1}^{i-1} a_{ij} = c_i$ для $i=2, \ldots, s$. Если требуется, чтобы метод имел порядок p, то следует так же обеспечить условие

$\bar\textbf{y}(h+x_0)-\textbf{y}(h+x_0)=O(h^{p+1}),$

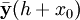где $\bar\textbf{y}(h+x_0)$ — приближение полученное по методу Рунге — Кутта. После многократного дифференцирования это условие преобразуется в систему полиномиальных уравнений на коэффициенты метода.

Произношение

Согласно грамматическим нормам русского языка фамилия Кутта́ склоняется^[4], поэтому говорят: "Метод Ру́нге — Кутты́ четвёртого порядка", так как законы русской грамматики предписывают склонять все мужские и женские фамилии, оканчивающиеся на -а, -я, которым предшествует согласный. Единственное исключение – фамилии французского происхождения с ударением на последнем слоге типа Дюма́, Золя́. Однако, в речевой практике зачастую встречается и несклоняемый вариант "Метод Ру́нге — Кутта́" (например, в книге^[5]). Как указывает Справочно-информационный портал Грамота.ру^[6], несклонение может быть оправдано тем, что фамилия Кутта́ имеет ударение на последнем слоге.

Решение систем ОДУ

Метод Рунге-Кутта непосредственно обобщается на случай систем обыкновенных дифференциальных уравнений.

Пример программы

Приведем пример программы на языке C#. В программе используется абстрактный класс TRungeKutta, в котором следует перекрыть абстрактный метод F, задающий правые части уравнений.

using System;
using System.Collections.Generic;
 
namespace rwsh_rk4
{
    public abstract class TRungeKutta 
    {
        public int N;
        double t; // текущее время 
        public double[] Y; // искомое решение Y[0] - само решение, Y[i] - i-тая производная решения
 
        double[] YY, Y1, Y2, Y3, Y4; // внутренние переменные 
 
        public TRungeKutta(int aN) // aN - размерность системы 
        {
            N = aN; // сохранить размерность системы
 
            if (N < 1)
            {
                N = -1; // если размерность меньше единицы, то установить флаг ошибки
                return; // и выйти из конструктора
            }
 
            Y = new double[N]; // создать вектор решения
            YY = new double[N]; // и внутренних решений
            Y1 = new double[N];
            Y2 = new double[N];
            Y3 = new double[N];
            Y4 = new double[N];
        }
 
        public void SetInit(double t0, double[] Y0) // установить начальные условия.
        {                                           // t0 - начальное время, Y0 - начальное условие
            t = t0;
            int i;
            for (i = 0; i < N; i++)
            {
                Y[i] = Y0[i];
            }
        }
 
        public double GetCurrent() // вернуть текущее время
        {
            return t;
        }
 
        public abstract void F(double t, double[] Y, ref double[] FY); // правые части системы.
 
        public void NextStep(double dt) // следующий шаг метода Рунге-Кутта, dt - шаг по времени (может быть переменным)
        {
            if(dt<0)
            {
                return;
            }
 
            int i;
 
            F(t, Y, ref Y1); // расчитать Y1
 
            for (i = 0; i < N; i++)
            {
                YY[i] = Y[i] + Y1[i] * (dt / 2.0);
            }
            F(t + dt / 2.0, YY, ref Y2); // расчитать Y2
 
            for (i = 0; i < N; i++)
            {
                YY[i] = Y[i] + Y2[i] * (dt / 2.0);
            }
            F(t + dt / 2.0, YY, ref Y3); // расчитать Y3
 
            for (i = 0; i < N; i++)
            {
                YY[i] = Y[i] + Y3[i] * dt;
            }
            F(t + dt, YY, ref Y4); // расчитать Y4
 
            for (i = 0; i < N; i++)
            {
                Y[i] = Y[i] + dt / 6.0 * (Y1[i] + 2.0 * Y2[i] + 2.0 * Y3[i] + Y4[i]); // расчитать решение на новом шаге
            }
 
            t = t + dt; // увеличить шаг
 
        }
    }
 
    public class TMyRK : TRungeKutta
    {
        public TMyRK(int aN) : base(aN) { }
 
        public override void F(double t, double[] Y, ref double[] FY) 
        {
            FY[0] = Y[1]; // пример математический маятник 
            FY[1] = -Y[0]; // y''(t)+y(t)=0
        }
    }
 
    class Program
    {
        static void Main(string[] args)
        {
            TMyRK RK4 = new TMyRK(2);
 
            double[] Y0 = {0, 1}; // зададим начальные условия y(0)=0, y'(0)=1
 
            RK4.SetInit(0, Y0);
 
            while (RK4.GetCurrent() < 10) // решаем до 10
            {
                Console.WriteLine("{0}\t{1}\t{2}", RK4.GetCurrent(), RK4.Y[0], RK4.Y[1]); // вывести t, y, y'
 
                RK4.NextStep(0.01); // расчитать на следующем шаге, шаг интегрирования dt=0.01
            }
        }
    }
}

См. также

• Метод Эйлера

Ссылки

1. ↑ Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. - М.: Бином, 2001 - с. 363-375.
2. ↑ Ильина В.А., Силаев П.К. Численные методы для физиков-теоретиков. т.2. - Москва-Ижевск: Институт компьютерных исследований, 2004. – с. 16-30.
3. ↑ ^{1 2} J. C. Butcher. Numerical Methods for Ordinary Differential Equations. The University of Auckland, New Zealand.
4. ↑ http://www.gramota.ru/spravka/buro/search_answer/?s=%F1%EB%EE%E3%E5, вопрос №255386.
5. ↑ Б. П. Демидович, И. А. Марон, Э. 3. Шувалова. Численные методы анализа, 3-е изд. - М.: Наука, 1967.
6. ↑ http://www.gramota.ru/spravka/buro/search_answer/?s=%D0%F3%ED%E3%E5, вопрос №255356.