- Классический метод расчета переходных процессов
-
Классический метод расчета переходных процессов
Название метода «классический» отражает использование в нем решений дифференциальных уравнений с постоянными параметрами методами классической математики. Данный метод обладает физической наглядностью и удобен для расчета простых цепей (расчет сложных цепей упрощается операторным методом).
Содержание
Методика
Этапы расчета переходного процесса в цепи классическим методом:
- Прежде всего необходимо составить систему уравнений на основе законов Кирхгофа, Ома, электромагнитной индукции и т.д., описывающих состояние цепи после коммутации, и исключением переменных получить одно дифференциальное уравнение, в общем случае неоднородное относительно искомого тока i или напряжения u. Для простых цепей получается дифференциальное уравнение первого или второго порядка, в котором в качестве искомой величины выбирают либо ток в индуктивном элементе, либо напряжение на емкостном элементе.
- Далее следует составить общее решение полученного неоднородного дифференциального уравнения цепи в виде суммы частного решения неоднородного дифференциального уравнения и общего решения соответствующего однородного дифференциального уравнения.
- Наконец, в общем решении следует найти постоянные интегрирования из начальных условий, т. е. услови в цепи в начальный момент времени после коммутации.
Применительно к электрическим цепям в качестве частного решения неоднородного дифференциального уравнения выбирают установившийся режим в рассматриваемой цепи (если он существует), т. е. постоянные токи и напряжения, если в цепи действуют источники постоянных ЭДС и токов, или синусоидальные напряжения и токи при действии источников синусоидальных ЭДС и токов. Токи и напряжения установившегося режима называют установившимися.
Общее решение однородного дифференциального уравнения описывает процесс в цепи без источников ЭДС и тока, который поэтому называют свободным процессом. Токи и напряжения свободного процесса называют свободными, а их выражения должны содержать постоянные интегрирования, число которых равно порядку однородного уравнения.
Примеры расчета
В схеме на рисунке до замыкания ключа был установившийся режим:
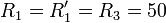 Ом, C = 100 мкФ, E = 150 В. Требуется найти: полные, принужденные и свободные составляющие токов i1,i2,i3 и uc при t = 0 + а также начальное значение производной от свободного напряжения на конденсаторе; токи i1,i2,i3 и напряжение uc в функции времени.
Ом, C = 100 мкФ, E = 150 В. Требуется найти: полные, принужденные и свободные составляющие токов i1,i2,i3 и uc при t = 0 + а также начальное значение производной от свободного напряжения на конденсаторе; токи i1,i2,i3 и напряжение uc в функции времени.До коммутации i2(0 − ) = 0 и
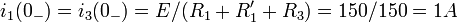 .
.Напряжение на конденсаторе равно напряжению на резисторе R3: Невозможно разобрать выражение (лексическая ошибка): u_c (0_-) = i_3 (0_-) R_3 = 1*50 = 50 В .
Найдем принужденные значения токов и напряжений после коммутации: Невозможно разобрать выражение (лексическая ошибка): i_{1пр} = i_{3пр} = \frac{E}{R_1 + R_3} = 150/150 = 1,5 A
Невозможно разобрать выражение (лексическая ошибка): u_{Cпр} (0_+) = i_{3пр} R_3 = 1,5*50 = 75 В .
См. также
Литература
- Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов.— 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6
Ссылки
- Классический метод расчета переходных процессов на http://www.ups-info.ru
- Методика и примеры расчета переходных процессов классическим методом. на http://www.ups-info.ru
Wikimedia Foundation. 2010.
