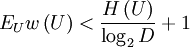Прямая теорема Шеннона для канала без помех

Не следует путать с другими теоремами Шеннона.

Теоремы Шеннона для источника общего вида описывают возможности кодирования источника общего вида с помощью разделимых кодов. Другими словами, описываются максимально достижимые возможности кодирования без потерь.

Прямая теорема

В применении к побуквенному кодированию прямая теорема может быть сформулирована следующим образом:

Существует префиксный, то есть разделимый код, для которого средняя длина сообщений отличается от нормированной энтропии не более, чем на единицу:

$E_U w\left( U \right) < \frac{{H\left( U \right)}}{{\log _2 D}} + 1$

где:

• U — некоторый источник сообщений, а также множество всех его сообщений u₁,u₂,...,u_K
• w₁,w₂,...,w_K — длины сообщений истоника после кодирования
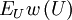• $E_U w\left( U \right)$ — средняя длина сообщений
• $H\left( U \right)$ — энтропия источника
• D — количество букв в алфавите кодирования (например, 2 для двоичного алфавита, 33 — для кодирования заглавными русскими буквами и т. д.)

В качестве доказательства теоремы исследуются характеристики кода Шеннона-Фано. Данный код удовлетворяет условиям теоремы, и он обладает указанными свойствами.

Обратная теорема

Обратная теорема ограничивает максимальную степень сжатия, достигаемую с помощью кодирования без потерь. В применении к побуквенному кодированию, описывает ограничение на среднюю длину кодового слова для любого разделимого кода.

Для любого разделимого кода с длинами w₁,w₂,...,w_K средняя длина сообщений больше или равна энтропии источника U, нормированный на двоичный логарифм от числа букв D в алфавите кодера:

$\frac{{H\left( U \right)}}{{\log _2 D}} \le E_U w\left( U \right)$

Литература

• Габидулин, Э. М., Пилипчук, Н. И. §3.4 Теоремы Шеннона для источника // Лекции по теории информации. — М.: МФТИ, 2007. — С. 49-52. — 214 с. — ISBN 5-7417-0197-3