Осцилляции Зенера — Блоха

Осцилляции Зенера — Блоха

Осцилляции Зенера — Блоха

Если пренебречь межзонными переходами электронов в присутствии внешнего электрического поля 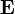$\mathbf{E}$, то перемещения электрона в k-пространстве полностью определяется вторым законом Ньютона:

$\hbar \; \frac{dk}{dt} = - e\mathbf{E}$.

Где e - элементарный заряд (в этих обозначениях заряд электрона равен $-e = -1,6 \cdot 10^{-19}$ Кл). При отсутствии столкновений электрон проходит во всей первой зоне Бриллюэна, отражается от её границы, снова пересекает зону, и вновь отражается на границе. В результате такое движение электрона в зоне под действием постоянного электрического поля имеет характер осцилляций в $\mathbf{k}$- пространстве, а значит и в обычном пространстве. Эти осцилляции получили название осцилляций Зенера (частичный случай электрического поля) и Блоха (общий случай действия потенциального поля какой-либо природы).

Пусть поле 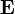$\mathbf{E}$ направлено вдоль вектора обратной решётки $\mathbf{K}$, определяющий положение границы зоны Бриллюэна, отражающей электроны. За одну осцилляцию электрон проходит расстояние K. Если $K = \frac{2\pi}{a}$, где a - постоянная решетки, то циклическая частота равна:

$\omega_z = \frac{eEa}{\hbar \;}$.

Поскольку $a \approx \; 3$A, для поля $2 \cdot 10^6$ В/м, то частота составляет около 10¹³ Гц. Осцилляции ограничены в пространстве. В такой ситуации потенциал возмущения $e\mathbf{E}\mathbf{r}$ видоизменяет энергетические уровни в зоне. И состояния, энергия которых отличается на величину eEa изменяют энергии вдоль краёв зоны. Равные энергии создают т. н. штарковскую лестницу, названную так, что её возникновение напоминает эффект Штарка в атомной физике. Ясно, что амплитуда L_z, пространственных осцилляций определяется шириной зоны W_b:

$L_z = \frac{ W_b }{2eE}$

Так как на элементарную ячейку приходится одно состояние, то общее количество осцилляций остаётся неизменной величиной, однако интервалы между соседними уровнями энергии остаются конечными и одинаковыми.

Волновая функция электрона в состоянии Зенера-Блоха, очевидно отличается от бегущей волны, поскольку $\mathbf{k}$ уже не является хорошим квантовым числом. Рассматривая приложенный потенциал, как возмущение, находим:

$\big (H^*_0 - e\mathbf{E}\cdot \mathbf{r} \big )\psi_z = E_z\psi_z$-

$\psi_z = V^{-\frac{1}{2}} \sum_{\mathbf{k}}^ \propto \; c_k\phi_k(\mathbf{r})$

где $\psi_k(\mathbf{r})$ - зонные функции Блоха. Теория возмущений даёт

$c_{k'} = \sum_{\mathbf{k}}^\propto \; \frac{c_k\left \langle \mathbf{k'}| - eE\mathbf{r}|\mathbf{k}\right \rangle}{W_z - W_{k'}}$

Матричный элемент удобнее всего вычислять учитывая

$\mathbf{r}exp(i\mathbf{k}\mathbf{r} ) = -i\Delta_k exp(i\mathbf{k}\mathbf{r})$

Переходя от суммирования по $\mathbf{k}$ к интегрированию с помощью соотношения

$\sum_{\mathbf{k}} \; \to \int_{}^{} \frac{V}{8\pi^3}\, d\mathbf{k}$

и интегрируя по частям, используя свойство ортогональности плоских волн, получаем:

$\sum_{\mathbf{k}}^ \propto \; c_k \left \langle \mathbf{k'}| - e\mathbf{E}\mathbf{r}|\mathbf{k} \right \rangle = -e \mathbf{E}\Delta_kc_k\delta_{kk'}$-

откуда находим производные

$\frac{dc_k}{d\mathbf{k}} = \frac{i(W_z - W_k)c_k}{eE}$

как и

$c_k = c_0 exp \quad \left \lbrace \int_{}^{} \frac{i(W_z - W_k)}{eE}\, d\mathbf{k} \right \rbrace$

С тем, чтобы периодичность волновой функции сохранялась, функция c_k должна быть периодической. Если положить

$W_k = W_0 + W(\mathbf{k}),$

где W_k = W₀ - энергия центра зоны, то с условия периодичности вытекает равенство энергий

$W_z - W_0 = e \mathbf{E}n'(\mathbf{a}),$

где n' - целое число, а 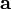$\mathbf{a}$- вектор элементарной ячейки. В результате, состояние, которому отвечает собственное значение W_z, локализовано в пространстве у элементарной ячейки, расположенной в точке $n'\mathbf{a}$, откуда полагая $n'\mathbf{a} = \mathbf{r}$, находим

$c_k = c_0 exp \quad \left \lbrace -i\big (\mathbf{k}\mathbf{r_0} \int_{}^{} \frac{iW_k}{eE}\, d\mathbf{k} \big )\right \rbrace$

Волновые функции Блоха здесь принимают вид

$\psi_z = V^{-1/2}c_0 \sum_{\mathbf{k}}^ \propto \; u_k(\mathbf{r}) exp \quad \left \lbrace i \int_{}^{}\frac{W(\mathbf{k})}{eE}\, d\mathbf{k} - i\mathbf{k}(\mathbf{r_0 - r}) \right \rbrace.$

Теперь можно использовать простую модель, описывающую зону по направлению поля $\mathbf{E}$:

$W\mathbf{k} = - \frac{W_b}{2} \cos ka \,$

$-\frac{\pi}{a} < k <\frac{\pi}{a},$

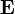где W_b- ширина зоны. Далее предполагаем, что функция $u_k(\mathbf{r})$ от $\mathbf{k}$. Тогда

$\psi_z = V^{-1/2}c_0 u(\mathbf{r})\sum_{\mathbf{k}}^ \propto \; exp \quad \left \lbrace -\frac{iW_b \sin {ka}}{2eEa} - i\mathbf{k} \mathbf{r_0 - r}\right \rbrace =$

$= c_0u(\mathbf{r})J_n(\frac{W_b}{2eEa}), n = (x_0 - x)/a,$

где J_n(z)- функция Бесселя, n- целое число, а поле направлено вдоль оси x. У точки x = x₀ функция J_n(z) ведет себя подобно стоящей волны с волновым вектором величины π / 2a, то есть длина волнового вектора ровная половине расстоянии от центра зоны Бриллюэна к его границе. Когда $|x_0 - x| \gg \, a$, асимптотическое разложение даёт

$J_n(\frac{W_b}{2eEa}) \approx \; \frac{(-1)^{|x_0-x|/a}}{(2\pi |x_0 - x|/a)^{1/2}}\big (\frac{e_nL_z}{2|x_0 - x|} \big)^{|x_0-x|/a}$

где L_z- классическая амплитуда пространственных осцилляций, а e_n- основание натуральных логарифмов. Ясно, которые у | x₀ − x | > e_nL_z / 2 волновая функция очень быстро затихают. Она уменьшается и $|x_0-x|\rightarrow 0$, достигая максимума при | x₀ − x | = L_z / 2. Поведение этой волновой функции качественно напоминает поведение гармоничного осцилятора - она растет у концов отрезка, соответствующие классическим точкам поворота. С тем, чтобы наблюдать это явление необходимо удовлетворить условия

ω_zτ > 1,

где τ- время между столкновениями. Обычно расчет времени τ проводят для состояний, близких к краям зоны. Типичные значения τ около 10 ^{− 13} с. В результате, электрон который осуществляет колебания Зинера-Блоха, большую часть времени находится около краёв зоны, и потому разумно принять оценку времени около 10 ^{− 13}. С целью необходимо создать поля превысят $2\cdot10^6$ В/м. Во многих случаях такое сильное поле может привести к пробою полупроводника.

Литература

• Ридли Б. Квантовые процессы в полупроводниках: Пер. с англ. М.:Мир, 1986.
• Zener C. Proc.Roy.Soc.А, v.145, p.523, 1934.

См. также

• Квантовый осциллятор
• Осцилляции Блоха