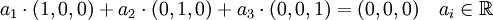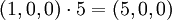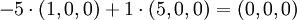- Линейно зависимые и линейно независимые системы векторов
-
В линейной алгебре линейная зависимость — это свойство, которое может иметь подмножество линейного пространства. Для этого должна существовать нетривиальная линейная комбинация элементов этого множества, равная нулевому элементу. Если такой комбинации нет, т.е. факторы единственной такой линейной комбинации равны нулю, множество называется линейно независимым.
Содержание
Пример
В
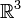 векторы (1,0,0), (0,1,0) и (0,0,1) линейно независимы, т.к. уравнение
векторы (1,0,0), (0,1,0) и (0,0,1) линейно независимы, т.к. уравнениеимеет только одно, тривиальное, решение. Векторы (1,0,0) и (5,0,0) являются линейно зависимыми, т.к.
а значит
Определение
Пусть V будет линейное пространство над полем K и
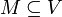 . M называется линейно независимым множеством, если любое его конечное подмножество является линейно независимым.
. M называется линейно независимым множеством, если любое его конечное подмножество является линейно независимым.Конечное множество M' = {v1,v2,...,vn} называется линейно независимым, если единственная линейная комбинация, равная нулю, тривиальна, т.е. состоит из факторов, равных нулю:

Если существует такая линейная комбинация с минимум одним
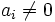 , M' называется линейно зависимым. Обратите внимание, что в первом равенстве подразумевается
, M' называется линейно зависимым. Обратите внимание, что в первом равенстве подразумевается 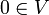 , а во втором
, а во втором 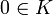 .
.Свойства
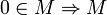 линейно зависимо
линейно зависимо- M линейно независимо
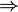 M' линейно независимо для всех
M' линейно независимо для всех 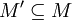
- M линейно зависимо
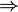 M' линейно зависимо для всех
M' линейно зависимо для всех 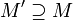
Значение
- Линейные системы уравнений
Линейная система n уравнений, где n — количество переменных, имеет однозначное решение тогда и только тогда, когда столбцы её основной матрицы являются линейно независимыми.
- Ранг матриц
Ранг матрицы равен числу её линейно независимых строк или столбцов.
- Геометрический смысл
- Векторы
 и
и 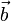 линейно зависимы тогда и только тогда, когда они коллинеарны (лежат на параллельных прямых).
линейно зависимы тогда и только тогда, когда они коллинеарны (лежат на параллельных прямых). - Векторы
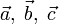 линейно зависимы тогда и только тогда, когда они компланарны (лежат в параллельных плоскостях).
линейно зависимы тогда и только тогда, когда они компланарны (лежат в параллельных плоскостях).
- Базис
Базис линейного пространства является в частности множеством линейно независимых векторов.
См. также
Wikimedia Foundation. 2010.