Ротор (математика)

У этого термина существуют и другие значения, см. Ротор.

Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем.

Обозначается

$\operatorname{rot}$ (в русскоязычной^[1] литературе) или

$\operatorname{curl}$ (в англоязычной литературе),

а также - как векторное умножение дифференциального оператора набла на векторное поле:

$\mathbf{\nabla} \times.$

Результат действия этого оператора на конкретное векторное поле F называется ротором поля F или, короче, просто ротором F и представляет собой новое векторное^[2] поле:

$\operatorname{rot}\,\mathbf F\equiv\mathbf{\nabla} \times \mathbf{F}.$

Поле rot F (длина и направление вектора rot F в каждой точке пространства) характеризует в некотором смысле^[3] вращательную составляющую поля F соответственно в каждой точке.

Интуитивный образ

Если v(x,y,z) - поле скорости движения газа (или течения жидкости), то rot v - вектор, пропорциональный вектору угловой скорости очень маленькой и лёгкой пылинки (или шарика), находящегося в потоке (и увлекаемого движением газа или жидкости; хотя центр шарика можно при желании закрепить, лишь бы он мог вокруг него свободно вращаться).

Конкретно rot v = 2 ω, где ω - эта угловая скорость.

• Простую иллюстрацию этого факта - см. ниже.

Эта аналогия может быть сформулирована вполне строго (см. ниже). Основное определение через циркуляцию (данное в следующем параграфе) можно считать эквивалентным полученному таким образом.

Математическое определение

Ротор $\operatorname{rot}\, \mathbf a$ векторного поля $\mathbf a$ — есть вектор, проекция которого $\operatorname{rot} _ \mathbf n \mathbf a$ на каждое направление n есть предел отношения циркуляции векторного поля по контуру L, являющемуся краем плоской площадки ΔS, перпендикулярной этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:

$\operatorname{rot} _ \mathbf n \mathbf a=\lim_{\Delta S\to 0}\frac{\oint\limits_{L}\mathbf{ a\cdot \, dr}}{\Delta S}$.

Направление обхода контура выбирается так, чтобы, если смотреть в направлении $\mathbf n$, контур L обходился по часовой стрелке^[4].

В трёхмерной декартовой системе координат ротор (в соответствии с определением выше) вычисляется следующим образом (здесь F - обозначено некое векторное поле с декартовыми компонентами $F_x, F_y, F_z$, а $\mathbf e_x, \mathbf e_y, \mathbf e_z$ - орты декартовых координат):

$\operatorname{rot}\;(F_x \mathbf e_x + F_y\, \mathbf e_y + F_z \mathbf e_z) =$

$= \left( \partial_y F_z - \partial_z F_y \right) \mathbf e_x+ \left( \partial_z F_x - \partial_x F_z \right) \mathbf e_y+ \left( \partial_x F_y - \partial_y F_x \right) \mathbf e_z \equiv$

$\equiv \left(\frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}\right) \mathbf e_x+ \left(\frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}\right) \mathbf e_y+ \left(\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}\right) \mathbf e_z.$

или

$(\operatorname{rot}\;\mathbf F)_x = \partial_y F_z - \partial_z F_y \equiv \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}$

$(\operatorname{rot}\;\mathbf F)_y = \partial_z F_x - \partial_x F_z \equiv \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}$

$(\operatorname{rot}\;\mathbf F)_z = \partial_x F_y - \partial_y F_x \equiv \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}$

(что можно считать альтернативным определением, по сути совпадающим с определением в начале параграфа, по крайней мере при условии дифференцируемости компонент поля).

Для удобства можно формально представлять ротор как векторное произведение оператора набла (слева) и векторного поля:

$\operatorname{rot}\; \mathbf{F} = \mathbf{\nabla} \times \mathbf{F} = \begin{pmatrix} \frac{\partial}{\partial x} \\ \\ \frac{\partial}{\partial y} \\ \\ \frac{\partial}{\partial z} \end{pmatrix} \times \mathbf F = \begin{vmatrix} \mathbf{e}_x & \mathbf{e}_y & \mathbf{e}_z \\ \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ \\ F_x & F_y & F_z \end{vmatrix}.$

(Последнее равенство формально представляет векторное произведение как определитель).

Связанные определения

Векторное поле, ротор которого равен нулю в любой точке, называется безвихревым и является потенциальным. Поскольку эти условия являются друг для друга необходимыми и достаточными, оба термина являются практическими синонимами. (Впрочем, это верно только для случая полей, определённых на односвязной области).

Чуть подробнее о взаимной обусловленности потенциальности и безвихревого характера поля - см. ниже (Основные свойства).

Напротив, поле, ротор которого не равен нулю, называется обычно вихревым, такое поле не может быть потенциальным.

Обобщение

Наиболее прямое обобщение ротора применительно к векторным (и псевдовекторным) полям, определённым на пространствах произвольной размерности (при условии совпадения размерности пространства с размерностью вектора поля) такое

$(\operatorname{rot}\;\mathbf F)_{12} = \left(\frac{\partial F_2}{\partial x_1} - \frac{\partial F_1}{\partial x_2}\right)$

$(\operatorname{rot}\;\mathbf F)_{13} = \left(\frac{\partial F_3}{\partial x_1} - \frac{\partial F_1}{\partial x_3}\right)$

$(\operatorname{rot}\;\mathbf F)_{23} = \left(\frac{\partial F_3}{\partial x_2} - \frac{\partial F_2}{\partial x_3}\right)$

...

или

$(\operatorname{rot}\;\mathbf F)_{mn} = \partial_m F_n - \partial_n F_m \equiv \frac{\partial F_n}{\partial x_m} - \frac{\partial F_m}{\partial x_n}$

при индексах m и n от 1 до размерности пространства.

Это же может быть записано как внешнее произведение:

$\operatorname{rot}\;\mathbf F = \nabla \wedge \mathbf F.$

• При этом ротор есть антисимметричное^[5] тензорное поле валентности два.

• В случае размерности 3 свертка этого тензора с символом Леви-Чивиты даёт обычное определение трехмерного ротора, приведённое в статье выше.

• Для двумерного пространства может быть вдобавок при желании использована аналогичная формула с псевдоскалярным произведением (такой ротор будет псевдоскаляром, совпадающим с проекцией традиционного векторного произведения на ось, ортогональную данному двумерному пространству - если считать при этом двумерное пространство вложенным в некое трехмерное, чтобы традиционное векторное произведение имело смысл).

Физическая интерпретация

По теореме Коши-Гельмгольца распределение скоростей сплошной среды вблизи точки О задаётся уравнением

$\mathbf{v}(\mathbf{r}) = \mathbf{v}_{O} + \mathbf{\omega} \times \mathbf{r} + \nabla\varphi + o(\mathbf{r}),$

где $\mathbf{\omega}$ — вектор углового вращения элемента среды в точке О, а $\varphi$ — квадратичная форма от координат — потенциал деформации элемента среды.

Таким образом, движение сплошной среды вблизи точки О складывается из поступательного движения (вектор $\mathbf{v}_{O}$), вращательного движения (вектор $\mathbf{\omega} \times \mathbf{r}$) и потенциального движения — деформации (вектор $\nabla\varphi$). Применяя к формуле Коши—Гельмгольца операцию ротора, получим, что в точке О справедливо равенство $\operatorname{rot} ~\mathbf{v} = 2\mathbf{\omega},$ и, следовательно, можно заключить, что когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.

В качестве интуитивного образа, как это описано выше, здесь можно использовать представление о вращении брошенной в поток маленькой пылинки (увлекаемой потоком с собой, без его заметного возмущения) или о вращении помещённого в поток с закреплённой осью маленького (без инерции, вращаемого потоком, заметно не искажая его) колеса с прямыми (не винтовыми) лопастями. Если то или другое при взгляде на него вращается против часовой стрелки, то это означает, что вектор ротора поля скорости потока в данной точке имеет положительную проекцию в направлении на нас.

Основные свойства

Свойства, непосредственно получаемые из обычных правил дифференцирования

• Линейность:

$\operatorname{rot}\;( a\mathbf{F} + b\mathbf{G} ) = a\;\operatorname{rot} ~\mathbf{F} + b\;\operatorname{rot} ~\mathbf{G}$

для любых векторных полей F и G и для любых постоянных чисел a и b.

• Если $\varphi$ — скалярное поле, а F — векторное, тогда:

$\operatorname{rot} ~\varphi \mathbf{F} = \operatorname{grad} ~\varphi ~\times \mathbf{F} + \varphi \;\operatorname{rot} ~\mathbf{F},$

или

$\nabla\times(\varphi \mathbf{F}) = (\nabla\varphi) \times \mathbf{F} + \varphi \;(\nabla\times\mathbf{F}).$

• Дивергенция ротора равна нулю:

$\operatorname{div} ~\operatorname{rot} ~\mathbf{F} = 0$ или $\nabla \cdot (\nabla \times \mathbf{F}) = 0 .$

При этом верно и обратное: если поле F бездивергентно, оно вихрь некоторого поля G (векторного потенциала):

$\operatorname{div} ~\mathbf{F} = 0 \Rightarrow \mathbf{F} = \operatorname{rot} ~\mathbf{G}.$

• Если поле F потенциально, его ротор равен нулю (поле F — безвихревое):

$\mathbf{F} = \operatorname{grad}~\varphi \Rightarrow \operatorname{rot} ~\mathbf{F} = 0$

Верно и обратное: если поле безвихревое, то оно потенциально:

$\operatorname{rot} ~\mathbf{F} = 0 \Rightarrow \mathbf{F} = \operatorname{grad}~\varphi$

для некоторого скалярного поля $\varphi\$ (то есть найдется такое $\varphi\$, что F будет его градиентом).

• (Следствие из свойств выше): два (и сколько угодно) различных векторных поля могут иметь одинаковый ротор. При этом различаться они будут обязательно на безвихревое поле, то есть на градиент некоторого скалярного поля.

• Ротор ротора равен градиенту дивергенции минус лапласиан:

$\operatorname{rot} ~\operatorname{rot} ~\mathbf{F} = \operatorname{grad} ~\operatorname{div} ~\mathbf{F} - \Delta\mathbf{F}$

Теорема Стокса

Циркуляция вектора по замкнутому контуру, являющемуся границей некоторой поверхности, равна потоку ротора этого вектора через эту поверхность:

$\oint\limits_{\partial S}\mathbf{F} \cdot\,\mathbf{dl} = \int\limits_S (\operatorname{rot} ~\mathbf{F}) \cdot \,\mathbf{dS}$

Частный случай теоремы Стокса для плоской поверхности - содержание теоремы Грина.

Альтернативные определения

Все определения ротора, о которых будет говориться в данном параграфе полностью эквивалентны (по крайней мере для случая дифференцируемого векторного поля), и в качестве основного, в принципе, можно выбрать любое из них. Остальные тогда оказываются формулами, которые могут быть более удобны в том или ином случае.

Прежде всего, перечислим явно те варианты, которые уже упоминались в статье выше и могут при желании каждое играть роль определения ротора.

• Классическое определение, приведённое в данной статье как основное (см.Математическое определение).
• Вычислительная формула через производные компонент в декартовых координатах, приведённая там же.
• Формула в параграфе Физическая интерпретация.

Кроме них полезно упомянуть:

• Выражение через символ Леви-Чивиты, дающее наиболее компактную координатную запись, а во втором варианте - общую формулу для любых криволинейных координат (ограничиваясь^[6], правда, только размерностью 3):
  • В варианте для ортонормированного базиса (обычных декартовых координат):

    $(\mathrm{rot}\ \mathbf v)_i = \sum_{j,k} \varepsilon_{ijk}\frac{\partial}{\partial x_j} v_k,$

  • В тензорной записи для произвольных (в том числе косоугольных и криволинейных координат; используя верхние и нижние индексы и правило суммирования Эйнштейна):

    $(\mathrm{rot}\ \mathbf v)_i = \varepsilon_{ijk}g^{jm}\frac{\partial}{\partial x^m} v^k,$

где $g^{jm}$ - метрический тензор в представлении с верхними индексами. В последнем случае (общем) важно упомянуть, что под значком $\varepsilon_{ijk}$ имеется в виду именно тензор, включая множитель $\sqrt{g}.$

• Интересную и довольно красивую форму определения, иногда используемую в литературе:

$\mathrm{rot}\ \mathbf a \Big|_{O} = \lim_{S\rightarrow O} \oint\limits_{S} [\mathbf a \times \mathbf{dS}].$

Ротор в криволинейных координатах

Общий случай

Удобным общим выражение ротора, пригодным для произвольных криволинейных координат в трехмерном^[6] пространстве является выражение с использованием тензора Леви-Чивиты:

Используя верхние и нижние индексы и правило суммирования Эйнштейна:

$(\mathrm{rot}\ \mathbf v)_i = \varepsilon_{ijk}g^{jm}\frac{\partial}{\partial x^m} v^k,$

где $\varepsilon_{ijk}$ - координатная запись тензора Леви-Чивиты, включая множитель $\sqrt{g},$ $g^{jm}$ - метрический тензор в представлении с верхними индексами, $g \equiv \mathrm{det} (g_{rs}).$

Это выражение при желании может быть также переписано, например, в виде:

$(\mathrm{rot}\ \mathbf v)^n = g^{ni}\varepsilon_{ijk}g^{jm}\frac{\partial}{\partial x^m} v^k,$

итд.

В ортогональных криволинейных координатах

$\operatorname{rot}\;\mathbf{A} = \operatorname{rot}\;(\mathbf{q_1}A_1 + \mathbf{q_2}A_2 + \mathbf{q_3}A_3) =$

$= \frac{1}{H_2H_3}\left[\frac{\partial}{\partial q_2}(A_3H_3) - \frac{\partial}{\partial q_3}(A_2H_2)\right]\mathbf{q_1}\ +$

$+\ \frac{1}{H_3H_1}\left[\frac{\partial}{\partial q_3}(A_1H_1) - \frac{\partial}{\partial q_1}(A_3H_3)\right]\mathbf{q_2}\ +$

$+\ \frac{1}{H_1H_2}\left[\frac{\partial}{\partial q_1}(A_2H_2) - \frac{\partial}{\partial q_2}(A_1H_1)\right]\mathbf{q_3},$

где H_i — коэффициенты Ламе.

Примеры

• В этой главе будем использовать для единичных векторов по осям (прямоугольных) декартовых координат использовать обозначение $\mathbf e_x, \mathbf e_y, \mathbf e_z.$

Простой пример

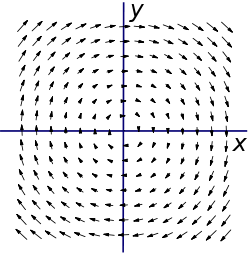
Рассмотрим векторное поле F, зависящее от координат x и y так:

$\mathbf{F}(x,y)=y\mathbf e_x - x \mathbf e_y$.

• В отношении этого примера нетрудно заметить, что $\mathbf{F} = \mathbf\omega \times \mathbf r$, где r - радиус-вектор, а $\omega = -1 \mathbf e_z$, то есть поле F можно рассматривать как поле скоростей точек твёрдого тела, вращающегося с единичной по величине угловой скоростью, направленной в отрицательном направлении оси z (то есть по часовой стрелке, если смотреть "сверху" - против оси z). Интуитивно более или менее очевидно, что поле закручено по часовой стрелке. Если мы поместим колесо с лопастями в жидкость, текущую с такими скоростями (то есть вращающуюся как целое по часовой стрелке), в любое место, мы увидим, что оно начнет вращаться по направлению часовой стрелки. (Для определения направлений используем, как обычно, правило правой руки или правого винта).
• z-компоненту поля F будем считать равной нулю. Однако если она ненулевая, но постоянная (или даже зависящая только от z) - результат для ротора, получаемый ниже, будет тем же.

Вычислим ротор:

$\mathbf{\nabla} \times \mathbf{F} =0 \mathbf e_x + 0 \mathbf e_y+ \left[ {\frac{\partial}{\partial x}}(-x) -{\frac{\partial}{\partial y}} y \right] \mathbf e_z = -2\mathbf e_z$

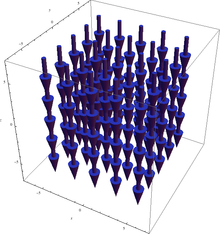
Как и предположили, направление совпало с отрицательным направлением оси z. В данном случае ротор оказался константой, то есть поле $\mathbf{\nabla} \times \mathbf{F}$ оказалось однородным, не зависящим от координат (что естественно для вращения твёрдого тела). Что замечательно,

• угловая скорость вращения жидкости, вычисленная из ротора и оказавшаяся равной точно $rot \mathbf F / 2$, точно совпала с тем, что указано в параграфе Физическая интерпретация, то есть этот пример является хорошей иллюстрацией приведённого там факта. (Конечно же, вычисления, полностью повторяющие приведённые выше, но только для неединичной угловой скорости, дают тот же результат $\mathbf{\nabla} \times \mathbf{F} = 2\omega$).

Угловая скорость вращения в данном примере одна и та же в любой точке пространства (угол поворота пылинки, приклеенной к твердому телу не зависит от того места, где именно приклеить пылинку). График ротора F поэтому не слишком интересен:

Более сложный пример

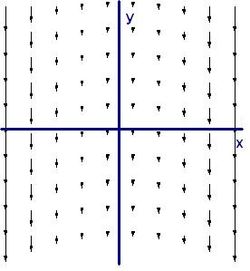
Теперь рассмотрим несколько более сложное векторное поле^[7]:

$F(x,y)=-x^2 \mathbf e_y$.

Его график:

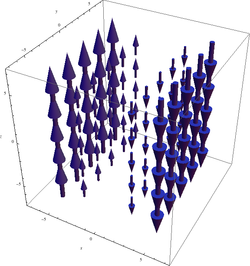
Мы можем не увидеть никакого вращения, но, посмотрев повнимательнее направо, мы видим большее поле в, например, точке x=4, чем в точке x=3. Если бы мы установили маленькое колесо с лопастями там, больший поток на правой стороне заставил бы колесо вращаться по часовой стрелке, что соответствует ввинчиванию в направлении -z. Если бы мы расположили колесо в левой части поля, больший поток на его левой стороне заставил бы колесо вращаться против часовой стрелки, что соответствует ввинчиванию в направлении +z. Проверим нашу догадку с помощью вычисления:

$\mathbf{\nabla} \times \mathbf{F} = 0 \mathbf e_x + 0 \mathbf e_y + {\frac{\partial}{\partial x}}(-x^2) \mathbf e_z = -2x \mathbf e_z$

Действительно, ввинчивание происходит в направлении +z для отрицательных x и -z для положительных x, как и ожидалось. Так как этот ротор не одинаков в каждой точке, его график выглядит немного интереснее:

Ротор F с плоскостью x=0, выделенной тёмно-синим цветом

Можно заметить, что график этого ротора не зависит от y или z (как и должно быть) и направлен по -z для положительных x и в направлении +z для отрицательных x.

Три общих примера

Основная статья: Формулы векторного анализа

Рассмотрим пример ∇ × [ v × F ]. Используя прямоугольную систему координат, можно показать, что

$\mathbf{ \nabla \times} \left( \mathbf{v \times F} \right) = \left[ \left( \mathbf{ \nabla \cdot F } \right) + \mathbf{F \cdot \nabla} \right] \mathbf{v}- \left[ \left( \mathbf{ \nabla \cdot v } \right) + \mathbf{v \cdot \nabla} \right] \mathbf{F} \ .$

Если v и ∇ поменять местами:

$\mathbf{v \ \times } \left( \mathbf{ \nabla \times F} \right) =\nabla_F \left( \mathbf{v \cdot F } \right) - \left( \mathbf{v \cdot \nabla } \right) \mathbf{ F} \ ,$

что является фейнмановской записью с нижним индексом ∇_F, что значит, что градиент с индексом F относится только к F.

Другой пример ∇ × [ ∇ × F ]. Используя прямоугольную систему координат, можно показать, что:

$\nabla \times \left( \mathbf{\nabla \times F} \right) = \mathbf{\nabla} (\mathbf{\nabla \cdot F}) - \nabla^2 \mathbf{F} \ ,$

что можно считать частным случаем первого примера с подстановкой v → ∇.

Поясняющие примеры

• В смерче ветры вращаются вокруг центра, и векторное поле скоростей ветра имеет ненулевой ротор (где-то) в центральной области. (см. Вихревое движение).
• Для векторного поля v скоростей движения точек вращающегося твёрдого (абсолютно твёрдого) тела, rot v одинаков всюду по объёму этого тела и равен (вектору) удвоенной угловой скорости вращения (подробнее - см. выше).
• Если бы скорости автомобилей на трассе описывались векторным полем, и разные полосы имели разные ограничения по скорости движения, ротор на границе между полосами был бы ненулевым.
• Закон электромагнитной индукции Фарадея, одно из уравнений Максвелла, просто записывается (в дифференциальной форме) через ротор: ротор электрического поля равен скорости изменения магнитного поля (со временем), взятой с обратным знаком.
• Четвёртое уравнение Максвелла - закон Ампера - Максвелла также записывается в дифференциальной форме с использованием ротора: ротор напряжённости магнитного поля равен сумме плотностей тока обычного и тока смещения.^[8]

Важный контринтуитивный пример

Довольно важно иметь в виду, что в принципе (хотя и далеко не всегда) направление ротора может не соответствовать направлению вращения поля (будем говорить для конкретности о поле скоростей жидкости), которое кажется очевидным по направлению искривления линий тока. Он может даже иметь противоположное направление (а в частном случае ротор может оказаться равным нулю, хотя линии тока загибаются или даже представляют собой точные окружности).

Дело в том, что ротор может быть представлен как сумма двух слагаемых, одно из которых завивит от кривизны линий тока, а второе от завивимости скорости течения от перпендикулярной (в данной точке) скорости течения координаты.

Рассмотрим частный, но хорошо иллюстрирующий сказанное пример. Пусть поле скорости течения жидкости v таково, что на любом фиксированном расстоянии r от некоторого фиксированного центра (поместим туда для удобства и начало координат) - жидкость течет точно по окружности с центром в начале координат и радиусом r (будем для краткости говорить в двумерных терминах; для перехода к трехмерной формулировке этого примера надо заменить слово "центр" на слово "ось").

Пусть скорость движения по каждой такой окружности (равная абсолютной величине вектора v) зависит только от r :

$v \equiv |\mathbf v| = v(r).$

Пусть направление вращения - против часовой стрелки (угловая скорость - вдоль оси z).

Нам будет досаточно вычислить ротор только вдоль оси x. Для этого выразим v (его компоненты) через координаты вблизи оси x.

$v_x = - v(x) y / x,\$

$v_y = v(x).\$

(Учитывая то, что вблизи оси x можем считать, что координата y << x, а при дифференцировании нам нужен будет только первый порядок, мы отбросили всё, меньшее y/x, и воспользовались тем, что вследствии этого x≈r).

Вычислим теперь прямо компоненту ротора на ось z:

$(rot\ \mathbf v)_z = \partial_x v_y - \partial_y v_x,$

что даст, если подставить сюда $v_x, v_y$ приведённые выше,

$(rot\ \mathbf v)_z = d v(x) / dx + v(x) / x.$

Отсюда видно, что

• Если v(r) ~ 1/r, то rot v = 0.
• Eсли v(r) убывает с r быстрее, чем 1/r, то проекция ротора на ось z отрицательна! (это и есть контринтуитивный пример).

Таким образом, мы видим, что в принципе просто из того, куда закручены линии тока не очевидно, куда направлен ротор такого течения. То есть не очевидно, в какую сторону будут вращаться пылинки в таком потоке. Зато достаточно ясно, что если где-то есть очень резкое убывание v(r), то направление ротора в этом месте будет направоено против того, которое соответствует направлению закручивания линий тока.

Этот частный пример означает, что и в общем случае однозначной связи между направлением закручивания линий поля и направлением вектора его ротора - нет.

Необходимо однако сделать две оговорки:

1. всё сказанное не означает, что однозначной связи между направлением закручивания линий поля и направлением вектора ротора этого поля не может быть для каких-то конкретных полей (подчиняющихся определённым уравнениям) и даже, быть может, для большинства практически важных полей в простых ситуациях. Однако если такая связь для каких-то (и даже для многих) полей имеет место, то
   1. во-первых, это есть следствие не определения ротора, а других уравнений (которые могут быть справедливы для какого-то конкретного поля и какой-то конкретной ситуации, а могут - для других полей ситуаций - и не быть),
   2. во-вторых, даже если эти другие уравнения в простейшем случае дадут такую связь, то при усложнении ситуации она может пропасть. Например, при переходе от случая однородной среды к неоднородной; так, даже если для однородной жидкости в бесконечном свободном пространстве такая связь имела бы место, то для вращения жидкости в неподвижном сосуде, скажем круглом стакане, очевидно вблизи стенок ротор будет противоположен направлению вращения жидкости в целом.
2. исходя из теоремы Стокса можно утверждать, что если (например) жидкость вращается по окружности, то где-то внутри этой окружности есть точки, в которых ротор имеет знак (направление), совпадающий с направлением циркуляции жидкости. В нашем примере быстроубывающего v(r), рассмотренном выше в этой главе, такая область находится вблизи центра (в предельном случае - в самом центре ротор даже становится бесконечным). Однако мы утверждаем (как это и видно из примера), что это совпадение не обязано существовать ни вблизи данной точки, ни даже везде внутри окружности данного радиуса (а лишь где-то внутри неё, хотя интеграл по всей её внутренности и даст таки это совпадение, то есть "в среднем" - направление совпадает; однако в большинстве точек - может быть и противоположным).

Примечания

1. ↑ Также в немецкой, откуда, по-видимому, это обозначение и попало в русскую, а также почти везде в Европе, кроме Англии, где такое обозначение считается "альтернативным".
2. ↑ Точнее - если F - псевдовекторное поле, то rot F - обычное векторное поле (вектор rot F - полярный), и наоборот, если поле F - поле обычного (полярного) вектора, то rot F - псевдовекторное поле.
3. ↑ См. далее.
4. ↑ Обычное соглашение, согласованное с определением через векторное произведение с оператором набла.
5. ↑ То, что тензор антисимметричен, очевидно непосредственно из определения.
6. ↑ ^{1 2} Для произвольной размерности - см. параграф «Обобщение».
7. ↑ Простейшая физическая реализация такого поля (с точностью до аддитивной константы, которая не влияет на вычисление ротора, поскольку rot const = 0; кроме того, при желании эта константа может быть обнулена переходом в систему отсчета, связанной с максимально быстро текущей водой в центре струи) - ламинарное течение (вязкой) жидкости между двумя параллельными твердыми плоскостями, перпендикулярными оси х, под действием однородного силового поля (тяжести) или разности давлений. Течение жидкости в трубе круглого сечения даёт такую же зависимости $v_y(x)$, поэтому приведённое дальше вычисление ротора применимо и к этому случаю (проще всего взять ось y совпадающей с осью трубы, и хотя зависимость $\mathbf v (z)$ не будет уже константой, однако $\partial v_y/\partial z$ будет нулем при z = 0, как и в основном примере, т.е. вычисление и ответ для любой плоскости, проходящей через ось трубы такой же, а это решает задачу).
8. ↑ Математический словарь высшей школы. В. Т. Воднев, А. Ф. Наумович, Н. Ф. Наумович

См. также

• Векторный анализ
• Дивергенция
• Оператор набла
• Теорема Грина
• Формулы векторного анализа