- Уравнения Максвелла
-
Уравне́ния Ма́ксвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца образуют полную систему уравнений классической электродинамики. Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее, влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму (одним из ярчайших примеров здесь может служить специальная теория относительности).
Содержание
- 1 История
- 2 Запись уравнений Максвелла и системы единиц
- 3 Дифференциальная форма
- 4 Интегральная форма
- 5 Сила Лоренца
- 6 Размерные константы в уравнениях Максвелла
- 7 Уравнения Максвелла в среде
- 8 Законы сохранения
- 9 Потенциалы
- 10 Ковариантная формулировка
- 11 Спектральное представление
- 12 Уравнения без свободных зарядов и токов
- 13 Некоторые точные решения
- 14 Связь с другими теориями
- 15 Аксиоматический подход
- 16 Единственность решений уравнений Максвелла
- 17 Численное решение уравнений Максвелла
- 18 Источники
- 19 Примечания
- 20 См. также
- 21 Литература
- 22 Ссылки
История
Уравнения, сформулированные Джеймсом Клерком Максвеллом, возникли на основе ряда важных экспериментальных открытий, которые были сделаны в начале XIX века. В 1820 году Ганс Христиан Эрстед обнаружил[1], что пропускаемый через провод гальванический ток заставляет отклоняться магнитную стрелку компаса. Это открытие привлекло широкое внимание учёных того времени. В том же 1820 году Био и Савар экспериментально нашли выражение[2] для порождаемой током магнитной индукции (закон Био — Савара), и Андре Мари Ампер обнаружил, что взаимодействие на расстоянии возникает также между двумя проводниками, по которым пропускается ток. Ампер ввёл термин «электродинамический» и выдвинул гипотезу, что природный магнетизм связан с существованием в магните круговых токов[3].
Влияние тока на магнит, обнаруженное Эрстедом, привело Майкла Фарадея к идее о том, что должно существовать обратное влияние магнита на токи. После длительных экспериментов, в 1831 году, Фарадей открыл, что перемещающийся возле проводника магнит порождает в проводнике электрический ток. Это явление было названо электромагнитной индукцией. Фарадей ввёл понятие «поля сил» — некоторой среды, находящейся между зарядами и токами. Его рассуждения носили качественный характер, однако они оказали огромное влияние на исследования Максвелла.
После открытий Фарадея стало ясно, что старые модели электромагнетизма (Ампер, Пуассон и др.) неполны. Вскоре появилась теория Вебера, основанная на дальнодействии. Однако к этому моменту вся физика, кроме теории тяготения, имела дело только с близкодейственными силами (оптика, термодинамика, механика сплошных сред и др.). Гаусс, Риман и ряд других учёных высказывали догадки, что свет имеет электромагнитную природу, так что теория электромагнитных явлений тоже должна быть близкодейственной. Этот принцип стал существенной особенностью теории Максвелла.
В своём знаменитом «Трактате об электричестве и магнетизме» (1873) Максвелл писал[4]:
Приступая к изучению труда Фарадея, я установил, что его метод понимания явлений был так же математическим, хотя и не представленным в форме обычных математических символов. Я также нашёл, что этот метод можно выразить в обычной математической форме и таким образом сравнить с методами профессиональных математиков.
Заменяя фарадеевский термин «поле сил» на понятие «напряжённость поля», Максвелл сделал его ключевым объектом своей теории[5]:
Если мы примем эту среду в качестве гипотезы, я считаю, что она должна занимать выдающееся место в наших исследованиях, и что нам следовало бы попытаться сконструировать рациональное представление о всех деталях её действия, что и было моей постоянной целью в этом трактате.
Подобная электродинамическая среда явилась абсолютно новым понятием для ньютоновской физики. Последняя изучала взаимодействие между собой материальных тел. Максвелл же записал уравнения, которым должна подчиняться среда, определяющая взаимодействие зарядов и токов и существующая даже в их отсутствие.
Анализируя известные эксперименты, Максвелл получил систему уравнений для электрического и магнитного полей. В 1855 году в своей самой первой статье «О фарадеевых силовых линиях»[6] («On Faraday’s Lines of Force»[7]) он впервые записал в дифференциальной форме систему уравнений электродинамики, но не вводя ещё ток смещения. Такая система уравнений описывала все известные к тому времени экспериментальные данные, но не позволяла связать между собой заряды и токи и предсказать электромагнитные волны[8]. Впервые ток смещения был введён Максвеллом в работе «О физических силовых линиях»[9] («On Physical Lines of Force»[10]), состоящей из четырёх частей и опубликованной в 1861—1862 годах. Обобщая закон Ампера, Максвелл вводит ток смещения, вероятно, чтобы связать токи и заряды уравнением непрерывности, которое уже было известно для других физических величин[8]. Следовательно, в этой статье фактически была завершена формулировка полной системы уравнений электродинамики. В статье 1864 года «Динамическая теория электромагнитного поля»[11] («A dynamical theory of the electromagnetic field»[12]) рассмотрена сформулированная ранее система уравнений из 20 скалярных уравнений для 20 скалярных неизвестных. В этой статье Максвелл впервые сформулировал понятие электромагнитного поля как физической реальности, имеющей собственную энергию и конечное время распространения, определяющее запаздывающий характер электромагнитного взаимодействия[8].
Оказалось, что не только ток, но и изменяющееся со временем электрическое поле (ток смещения) порождает магнитное поле. В свою очередь, в силу закона Фарадея, изменяющееся магнитное поле снова порождает электрическое. В результате, в пустом пространстве может распространяться электромагнитная волна. Из уравнений Максвелла следовало, что её скорость равна скорости света, поэтому Максвелл сделал вывод об электромагнитной природе света.
Часть физиков выступила против теории Максвелла (особенно много возражений вызвала концепция тока смещения). Гельмгольц предложил свою теорию, компромиссную по отношению к моделям Вебера и Максвелла, и поручил своему ученику Генриху Герцу провести её экспериментальную проверку. Однако опыты Герца однозначно подтвердили правоту Максвелла.
Максвелл не использовал векторных обозначений и записывал свои уравнения в достаточно громоздком компонентном виде. В своём трактате[13] он, кроме того, частично использовал кватернионную формулировку. Современная форма уравнений Максвелла появилась около 1884 года после работ Хевисайда, Герца и Гиббса. Они не только переписали систему Максвелла в векторном виде, но и симметризовали её, переформулировав в терминах поля, избавившись от электрического и магнитного потенциалов, игравших в теории Максвелла существенную роль, поскольку полагали, что эти функции являются лишь ненужными вспомогательными математическими абстракциями[14]. Интересно, что современная физика поддерживает Максвелла, но не разделяет негативное отношение его ранних последователей к потенциалам. Электромагнитный потенциал играет важную роль в квантовой физике и проявляется как физически измеряемая величина в некоторых экспериментах, например, в эффекте Ааронова — Бома[15].
Система уравнений в формулировке Герца и Хевисайда некоторое время называлась уравнениями Герца — Хевисайда[16]. Эйнштейн в классической статье «К электродинамике движущихся тел»[17] назвал их уравнениями Максвелла — Герца. Иногда в литературе встречается также название уравнения Максвелла — Хевисайда[18].
Уравнения Максвелла сыграли важную роль при возникновении специальной теории относительности (СТО). Джозеф Лармор (1900 год)[19] и независимо от него Хенрик Лоренц (1904 год)[20] нашли преобразования координат, времени и электромагнитных полей, которые оставляют уравнения Максвелла инвариантными при переходе от одной инерциальной системы отсчёта к другой. Эти преобразования отличались от преобразований Галилея классической механики и, следуя Анри Пуанкаре[21], стали называться преобразованиями Лоренца. Они стали математическим фундаментом специальной теории относительности.
Распространение электромагнитных волн со скоростью света первоначально интерпретировалось как возмущения некоторой среды, так называемого эфира[22]. Были предприняты многочисленные попытки (см.исторический обзор) обнаружить движение Земли относительно эфира, однако они неизменно давали отрицательный результат.[23] Поэтому Анри Пуанкаре высказал гипотезу о принципиальной невозможности обнаружить подобное движение (принцип относительности). Ему же принадлежит постулат о независимости скорости света от скорости его источника и вывод (вместе с Лоренцем), исходя из сформулированного так принципа относительности, точного вида преобразований Лоренца (при этом были показаны и групповые свойства этих преобразований). Эти две гипотезы (постулата) легли и в основу статьи Альберта Эйнштейна (1905 год)[17]. С их помощью он также вывел преобразования Лоренца и утвердил их общефизический смысл, особо подчеркнув возможность их применения для перехода из любой инерциальной системы отсчета в любую другую инерциальную. Эта работа фактически ознаменовала собой построение специальной теории относительности. В СТО преобразования Лоренца отражают общие свойства пространства и времени, а модель эфира оказывается ненужной. Электромагнитные поля являются самостоятельными объектами, существующими наравне с материальными частицами.
Классическая электродинамика, основанная на уравнениях Максвелла, лежит в основе многочисленных приложений электро- и радиотехники, СВЧ и оптики. До настоящего времени не было обнаружено ни одного эффекта, который потребовал бы видоизменения уравнений. Они оказываются применимы и в квантовой механике, когда рассматривается движение, например, заряженных частиц во внешних электромагнитных полях. Поэтому уравнения Максвелла являются основой микроскопического описания электромагнитных свойств вещества.
Уравнения Максвелла востребованы также в астрофизике и космологии, поскольку многие планеты и звезды обладают магнитным полем. Магнитное поле определяет, в частности, свойства таких объектов, как пульсары и квазары.
На современном уровне понимания все фундаментальные частицы являются квантовыми возбуждениями («квантами») различных полей. Например, фотон — это квант электромагнитного поля, а электрон — квант спинорного поля[24]. Поэтому полевой подход, предложенный Фарадеем и существенно развитый Максвеллом, является основой современной физики фундаментальных частиц, в том числе её стандартной модели.
- Исторически несколько раньше он сыграл важную роль в появлении квантовой механики в формулировке Шрёдингера и вообще открытии квантовых уравнений, описывающих движение частиц, в том числе и релятивистских (уравнение Клейна — Гордона, уравнение Дирака), хотя первоначально аналогия с уравнениями Максвелла здесь виделась скорее лишь в общей идее, тогда как впоследствии оказалось, что она может быть понята как более конкретная и детальная (как это описано выше).
Также полевой подход, в целом восходящий к Фарадею и Максвеллу, стал центральным в теории гравитации (включая ОТО).
Запись уравнений Максвелла и системы единиц
Запись большинства уравнений в физике не зависит от выбора системы единиц. Однако в электродинамике это не так. В зависимости от выбора системы единиц в уравнениях Максвелла возникают различные коэффициенты (константы). Международная система единиц (СИ) является стандартом в технике и преподавании, однако споры среди физиков о её достоинствах и недостатках по сравнению с конкурирующей симметричной гауссовой системой единиц (СГС) не утихают[25]. Преимущество системы СГС в электродинамике состоит в том, что все поля в ней имеют одну размерность, а уравнения, по мнению многих учёных, записываются проще и естественней[26]. Поэтому СГС продолжает применяться в научных публикациях по электродинамике и в преподавании теоретической физики, например, в курсе теоретической физики Ландау и Лифшица. Однако для практических применений вводимые в СГС единицы измерений, многие из которых неименованы и неоднозначны, часто неудобны. Система СИ стандартизована и лучше самосогласованна, на этой системе построена вся современная метрология[27]. Кроме того, система СИ обычно используется в курсах общей физики. В связи с этим все соотношения, если они по-разному записываются в системах СИ и СГС, далее приводятся в двух вариантах.
Дифференциальная форма
Уравнения Максвелла представляют собой в векторной записи систему из четырёх уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных[28]) линейных дифференциальных уравнений в частных производных первого порядка для 12 компонент четырёх векторных функций (
 ):
):Название СГС СИ Примерное словесное выражение Закон Гаусса Электрический заряд является источником электрической индукции. Закон Гаусса для магнитного поля Не существует магнитных зарядов.[~ 1] Закон индукции Фарадея Изменение магнитной индукции порождает вихревое электрическое поле.[~ 1] Теорема о циркуляции магнитного поля Электрический ток и изменение электрической индукции порождают вихревое магнитное поле Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные.
Введённые обозначения:
 — плотность стороннего электрического заряда (в единицах СИ — Кл/м³);
— плотность стороннего электрического заряда (в единицах СИ — Кл/м³); — плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае — случае тока, порождаемого одним типом носителей заряда, она выражается просто как
— плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае — случае тока, порождаемого одним типом носителей заряда, она выражается просто как  , где
, где  — (средняя) скорость движения этих носителей в окрестности данной точки,
— (средняя) скорость движения этих носителей в окрестности данной точки,  — плотность заряда этого типа носителей (она в общем случае не совпадает с
— плотность заряда этого типа носителей (она в общем случае не совпадает с  )[29]; в общем случае это выражение надо усреднить по разным типам носителей;
)[29]; в общем случае это выражение надо усреднить по разным типам носителей; — скорость света в вакууме (299 792 458 м/с);
— скорость света в вакууме (299 792 458 м/с); — напряжённость электрического поля (в единицах СИ — В/м);
— напряжённость электрического поля (в единицах СИ — В/м); — напряжённость магнитного поля (в единицах СИ — А/м);
— напряжённость магнитного поля (в единицах СИ — А/м); — электрическая индукция (в единицах СИ — Кл/м²);
— электрическая индукция (в единицах СИ — Кл/м²); — магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с−2•А−1);
— магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с−2•А−1); — дифференциальный оператор набла, при этом:
— дифференциальный оператор набла, при этом:
 означает ротор вектора,
означает ротор вектора, означает дивергенцию вектора.
означает дивергенцию вектора.
Приведённые выше уравнения Максвелла не составляют ещё полной системы уравнений электромагнитного поля, поскольку они не содержат свойств среды, в которой возбуждено электромагнитное поле. Соотношения, связывающие величины
 ,
,  ,
,  ,
,  и
и  и учитывающие индивидуальные свойства среды, называются материальными уравнениями.
и учитывающие индивидуальные свойства среды, называются материальными уравнениями.Интегральная форма
При помощи формул Остроградского — Гаусса и Стокса дифференциальным уравнениям Максвелла можно придать форму интегральных уравнений:
Название СГС СИ Примерное словесное выражение Закон Гаусса Поток электрической индукции через замкнутую поверхность  пропорционален величине свободного заряда, находящегося в объёме
пропорционален величине свободного заряда, находящегося в объёме  , который окружает поверхность
, который окружает поверхность  .
.Закон Гаусса для магнитного поля Поток магнитной индукции через замкнутую поверхность равен нулю (магнитные заряды не существуют). Закон индукции Фарадея Изменение потока магнитной индукции, проходящего через незамкнутую поверхность  , взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре
, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре  , который является границей поверхности
, который является границей поверхности  .
.Теорема о циркуляции магнитного поля Полный электрический ток свободных зарядов и изменение потока электрической индукции через незамкнутую поверхность  , пропорциональны циркуляции магнитного поля на замкнутом контуре
, пропорциональны циркуляции магнитного поля на замкнутом контуре  , который является границей поверхности
, который является границей поверхности  .
.Введённые обозначения:
 — двумерная замкнутая в случае теоремы Гаусса поверхность, ограничивающая объём
— двумерная замкнутая в случае теоремы Гаусса поверхность, ограничивающая объём  , и открытая поверхность в случае законов Фарадея и Ампера — Максвелла (её границей является замкнутый контур
, и открытая поверхность в случае законов Фарадея и Ампера — Максвелла (её границей является замкнутый контур  ).
). — электрический заряд, заключённый в объёме
— электрический заряд, заключённый в объёме  , ограниченном поверхностью
, ограниченном поверхностью  (в единицах СИ — Кл);
(в единицах СИ — Кл); — электрический ток, проходящий через поверхность
— электрический ток, проходящий через поверхность  (в единицах СИ — А).
(в единицах СИ — А).
При интегрировании по замкнутой поверхности вектор элемента площади
 направлен из объёма наружу. Ориентация
направлен из объёма наружу. Ориентация  при интегрировании по незамкнутой поверхности определяется направлением правого винта, «вкручивающегося» при повороте в направлении обхода контурного интеграла по
при интегрировании по незамкнутой поверхности определяется направлением правого винта, «вкручивающегося» при повороте в направлении обхода контурного интеграла по  .
.Словесное описание законов Максвелла, например, закона Фарадея, несёт отпечаток традиции, поскольку вначале при контролируемом изменении магнитного потока регистрировалось возникновение электрического поля (точнее электродвижущей силы). В общем случае в уравнениях Максвелла (как в дифференциальной, так и в интегральной форме) векторные функции
 являются равноправными неизвестными величинами, определяемыми в результате решения уравнений.
являются равноправными неизвестными величинами, определяемыми в результате решения уравнений.Сила Лоренца
При решении уравнений Максвелла распределения зарядов
 и токов
и токов  часто считаются заданными. С учётом граничных условий и материальных уравнений это позволяет определить напряжённость электрического поля
часто считаются заданными. С учётом граничных условий и материальных уравнений это позволяет определить напряжённость электрического поля  и магнитную индукцию
и магнитную индукцию  , которые, в свою очередь, определяют силу, действующую на пробный заряд
, которые, в свою очередь, определяют силу, действующую на пробный заряд  , двигающийся со скоростью
, двигающийся со скоростью  . Эта сила называется силой Лоренца:
. Эта сила называется силой Лоренца:СГС СИ Электрическая составляющая силы направлена по электрическому полю (если
 ), а магнитная — перпендикулярна скорости заряда и магнитной индукции. Впервые выражение для силы, действующей на заряд в магнитном поле (электрическая компонента была известна), получил в 1889 году Хевисайд[30][31] за три года до Хендрика Лоренца, который вывел выражение для этой силы в 1892 году.
), а магнитная — перпендикулярна скорости заряда и магнитной индукции. Впервые выражение для силы, действующей на заряд в магнитном поле (электрическая компонента была известна), получил в 1889 году Хевисайд[30][31] за три года до Хендрика Лоренца, который вывел выражение для этой силы в 1892 году.В более сложных ситуациях в классической и квантовой физике в случае, когда под действием электромагнитных полей свободные заряды перемещаются и изменяют значения полей, необходимо решение самосогласованной системы из уравнений Максвелла и уравнений движения, включающих силы Лоренца. Получение точного аналитического решения такой полной системы сопряжено обычно с большими сложностями.
Размерные константы в уравнениях Максвелла
В гауссовой системе единиц СГС все поля имеют одинаковую размерность, и в уравнениях Максвелла фигурирует единственная фундаментальная константа
 , имеющая размерность скорости, которая сейчас называется скоростью света (именно равенство этой константы скорости распространения света дало Максвеллу основания для гипотезы об электромагнитной природе света[32]).
, имеющая размерность скорости, которая сейчас называется скоростью света (именно равенство этой константы скорости распространения света дало Максвеллу основания для гипотезы об электромагнитной природе света[32]).В системе единиц СИ, чтобы связать электрическую индукцию и напряжённость электрического поля в вакууме, вводится электрическая постоянная
 (
( ). Магнитная постоянная
). Магнитная постоянная  является таким же коэффициентом пропорциональности для магнитного поля в вакууме (
является таким же коэффициентом пропорциональности для магнитного поля в вакууме ( ). Названия электрическая постоянная и магнитная постоянная сейчас стандартизованы[33]. Ранее для этих величин также использовались, соответственно, названия диэлектрическая и магнитная проницаемости вакуума.
). Названия электрическая постоянная и магнитная постоянная сейчас стандартизованы[33]. Ранее для этих величин также использовались, соответственно, названия диэлектрическая и магнитная проницаемости вакуума.Скорость электромагнитного излучения в вакууме (скорость света) в СИ появляется при выводе волнового уравнения:

В системе единиц СИ, в качестве точных размерных констант определены скорость света в вакууме
 и магнитная постоянная
и магнитная постоянная  . Через них выражается электрическая постоянная
. Через них выражается электрическая постоянная  .
.Принятые значения[34] скорости света, электрической и магнитной постоянных приведены в таблице:
Символ Наименование Численное значение Единицы измерения СИ - Постоянная скорости света
 (точно)
(точно)
- Магнитная постоянная
- Гн/м
- Электрическая постоянная
- Ф/м
Иногда вводится величина, называемая «волновым сопротивлением», или «импедансом» вакуума:
 Ом.
Ом.Приближённое значение для
 получается, если для скорости света принять значение
получается, если для скорости света принять значение  м/c. В системе СГС
м/c. В системе СГС  . Эта величина имеет смысл отношения амплитуд напряжённостей электрического и магнитного полей плоской электромагнитной волны в вакууме.
. Эта величина имеет смысл отношения амплитуд напряжённостей электрического и магнитного полей плоской электромагнитной волны в вакууме.Уравнения Максвелла в среде
Чтобы получить полную систему уравнений электродинамики, к системе уравнений Максвелла необходимо добавить материальные уравнения, связывающие величины
 ,
,  ,
,  ,
,  ,
,  , в которых учтены индивидуальные свойства среды. Способ получения материальных уравнений дают молекулярные теории поляризации, намагниченности и электропроводности среды, использующие идеализированные модели среды. Применяя к ним уравнения классической или квантовой механики, а также методы статистической физики, можно установить связь между векторами
, в которых учтены индивидуальные свойства среды. Способ получения материальных уравнений дают молекулярные теории поляризации, намагниченности и электропроводности среды, использующие идеализированные модели среды. Применяя к ним уравнения классической или квантовой механики, а также методы статистической физики, можно установить связь между векторами  ,
,  ,
,  с одной стороны и
с одной стороны и  ,
,  с другой стороны.
с другой стороны.Связанные заряды и токи
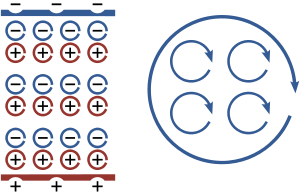 Слева: Совокупность микроскопических диполей в среде образуют один макроскопический дипольный момент и эквивалентны двум заряженным с противоположным знаком пластинам на границе. При этом внутри среды все заряды скомпенсированы; Справа: Совокупность микроскопических циркулярных токов в среде эквивалентна макроскопическому току, циркулирующему вдоль границы. При этом внутри среды все токи скомпенсированы.
Слева: Совокупность микроскопических диполей в среде образуют один макроскопический дипольный момент и эквивалентны двум заряженным с противоположным знаком пластинам на границе. При этом внутри среды все заряды скомпенсированы; Справа: Совокупность микроскопических циркулярных токов в среде эквивалентна макроскопическому току, циркулирующему вдоль границы. При этом внутри среды все токи скомпенсированы.
При приложении электрического поля к диэлектрическому материалу каждая из его молекул превращается в микроскопический диполь. При этом положительные ядра атомов немного смещаются в направлении поля, а электронные оболочки в противоположном направлении. Кроме этого, молекулы некоторых веществ изначально имеют дипольный момент. Дипольные молекулы стремятся ориентироваться в направлении поля. Этот эффект называется поляризацией диэлектриков. Такое смещение связанных зарядов молекул в объёме эквивалентно появлению некоторого распределения зарядов на поверхности, хотя все молекулы, вовлечённые в процесс поляризации остаются нейтральными (см. рисунок).
Аналогичным образом происходит магнитная поляризация (намагничивание) в материалах, в которых составляющие их атомы и молекулы имеют магнитные моменты, связанные со спином и орбитальным моментом ядер и электронов. Угловые моменты атомов можно представить в виде циркулярных токов. На границе материала совокупность таких микроскопических токов эквивалентна макроскопическим токам, циркулирующим вдоль поверхности, несмотря на то, что движение зарядов в отдельных магнитных диполях происходит лишь в микромасштабе (связанные токи).
Рассмотренные модели показывают, что хотя внешнее электромагнитное поле действует на отдельные атомы и молекулы, его поведение во многих случаях можно рассматривать упрощённым образом в макроскопическом масштабе, игнорируя детали микроскопической картины.
В среде сторонние электрические и магнитные поля вызывают поляризацию и намагничивание вещества, которые макроскопически описываются соответственно вектором поляризации
 и вектором намагниченности
и вектором намагниченности  вещества, а вызваны появлением связанных зарядов
вещества, а вызваны появлением связанных зарядов  и токов
и токов  . В результате поле в среде оказывается суммой внешних полей и полей, вызванных связанными зарядами и токами.
. В результате поле в среде оказывается суммой внешних полей и полей, вызванных связанными зарядами и токами.СГС СИ Поляризация
 и намагниченность вещества
и намагниченность вещества  связаны с векторами напряжённости и индукции электрического и магнитного поля следующими соотношениями:
связаны с векторами напряжённости и индукции электрического и магнитного поля следующими соотношениями:СГС СИ Поэтому, выражая векторы
 и
и  через
через  ,
,  ,
,  и
и  , можно получить математически эквивалентную систему уравнений Максвелла:
, можно получить математически эквивалентную систему уравнений Максвелла:СГС СИ Индексом
 здесь обозначены свободные заряды и токи. Уравнения Максвелла в такой форме являются фундаментальными, в том смысле, что они не зависят от модели электромагнитного устройства вещества. Разделение зарядов и токов на свободные и связанные позволяет «спрятать» в
здесь обозначены свободные заряды и токи. Уравнения Максвелла в такой форме являются фундаментальными, в том смысле, что они не зависят от модели электромагнитного устройства вещества. Разделение зарядов и токов на свободные и связанные позволяет «спрятать» в  ,
,  , а затем в
, а затем в  и, следовательно, в
и, следовательно, в  сложный микроскопический характер электромагнитного поля в среде.
сложный микроскопический характер электромагнитного поля в среде.Материальные уравнения
Материальные уравнения устанавливают связь между
 и
и  . При этом учитываются индивидуальные свойства среды. На практике в материальных уравнениях обычно используются экспериментально определяемые коэффициенты (зависящие в общем случае от частоты электромагнитного поля), которые собраны в различных справочниках физических величин[35].
. При этом учитываются индивидуальные свойства среды. На практике в материальных уравнениях обычно используются экспериментально определяемые коэффициенты (зависящие в общем случае от частоты электромагнитного поля), которые собраны в различных справочниках физических величин[35].- В слабых электромагнитных полях, сравнительно медленно меняющихся в пространстве и во времени, в случае изотропных, неферромагнитных и несегнетоэлектрических сред справедливо приближение, в котором поляризуемость и намагниченность линейно зависят от приложенных полей:
СГС СИ где введены безразмерные константы:
 — диэлектрическая восприимчивость и
— диэлектрическая восприимчивость и  — магнитная восприимчивость вещества (в системе единиц СИ эти константы в
— магнитная восприимчивость вещества (в системе единиц СИ эти константы в  раз больше, чем в гауссовой системе СГС). Соответственно, материальные уравнения для электрической и магнитной индукций записываются в следующем виде:
раз больше, чем в гауссовой системе СГС). Соответственно, материальные уравнения для электрической и магнитной индукций записываются в следующем виде:СГС СИ где
 — относительная диэлектрическая проницаемость,
— относительная диэлектрическая проницаемость,  — относительная магнитная проницаемость. Размерные величины
— относительная магнитная проницаемость. Размерные величины  (в единицах СИ — Ф/м) и
(в единицах СИ — Ф/м) и  (в единицах СИ — Гн/м), возникающие в системе СИ, называются абсолютная диэлектрическая проницаемость и абсолютная магнитная проницаемость соответственно.
(в единицах СИ — Гн/м), возникающие в системе СИ, называются абсолютная диэлектрическая проницаемость и абсолютная магнитная проницаемость соответственно.- В проводниках существует связь между плотностью тока и напряжённостью электрического поля, в хорошем приближении выражаемая законом Ома:

где
 — удельная проводимость среды (в единицах СИ — Ом−1•м−1).
— удельная проводимость среды (в единицах СИ — Ом−1•м−1).- В анизотропной среде
 ,
,  и
и  являются тензорами
являются тензорами  ,
,  и
и  . В системе координат главных осей они могут быть описаны диагональными матрицами. В этом случае, связь между напряжённостями полей и индукциями имеют различные коэффициенты по каждой координате. Например, в системе СИ:
. В системе координат главных осей они могут быть описаны диагональными матрицами. В этом случае, связь между напряжённостями полей и индукциями имеют различные коэффициенты по каждой координате. Например, в системе СИ:
![\begin{array}{lll}
D_x = \varepsilon_{0}\varepsilon_{xx}\,E_x,~~~~~ &
D_y = \varepsilon_{0}\varepsilon_{yy}\,E_y,~~~~~ &
D_z = \varepsilon_{0}\varepsilon_{zz}\,E_z, \\ [3mm]
B_x = \mu_0\mu_{xx}\,H_x,~~~~~ &
B_y = \mu_0\mu_{yy}\,H_y,~~~~~ &
B_z = \mu_0\mu_{zz}\,H_z.
\end{array}](2e4f54422b0c185b8f2c49e901237345.png)
- Хотя для широкого класса веществ линейное приближение для слабых полей выполняется с хорошей точностью, в общем случае зависимость между
 и
и  может быть нелинейной. В этом случае проницаемости среды не являются константами, а зависят от величины поля в данной точке. Кроме того, более сложная связь между
может быть нелинейной. В этом случае проницаемости среды не являются константами, а зависят от величины поля в данной точке. Кроме того, более сложная связь между  и
и  наблюдается в средах с пространственной или временной дисперсиями. В случае пространственной дисперсии токи и заряды в данной точке пространства зависят от величины поля не только в той же точке, но и в соседних точках. В случае временной дисперсии поляризация и намагниченность среды не определяются только величиной поля в данный момент времени, а зависят также от величины полей в предшествующие моменты времени. В самом общем случае нелинейных и неоднородных сред с дисперсией, материальные уравнения в системе СИ принимают интегральный вид:
наблюдается в средах с пространственной или временной дисперсиями. В случае пространственной дисперсии токи и заряды в данной точке пространства зависят от величины поля не только в той же точке, но и в соседних точках. В случае временной дисперсии поляризация и намагниченность среды не определяются только величиной поля в данный момент времени, а зависят также от величины полей в предшествующие моменты времени. В самом общем случае нелинейных и неоднородных сред с дисперсией, материальные уравнения в системе СИ принимают интегральный вид:


Аналогичные уравнения получаются в гауссовой системе СГС (если формально положить
 ).
).Уравнения в изотропных и однородных средах без дисперсии
В изотропных и однородных средах без дисперсии уравнения Максвелла принимают следующий вид:
СГС СИ В оптическом диапазоне частот вместо диэлектрической проницаемости
 используется показатель преломления
используется показатель преломления  (зависящий от длины волны), показывающий отличие скорости распространения монохроматической световой волны в среде от скорости света в вакууме. При этом в оптическом диапазоне диэлектрическая проницаемость обычно заметно меньше чем на низких частотах, а магнитная проницаемость большинства оптических сред практически равна единице. Показатель преломления большинства прозрачных материалов составляет от 1 до 2, достигая 5 у некоторых полупроводников[36]. В вакууме и диэлектрическая, и магнитная проницаемости равны единице:
(зависящий от длины волны), показывающий отличие скорости распространения монохроматической световой волны в среде от скорости света в вакууме. При этом в оптическом диапазоне диэлектрическая проницаемость обычно заметно меньше чем на низких частотах, а магнитная проницаемость большинства оптических сред практически равна единице. Показатель преломления большинства прозрачных материалов составляет от 1 до 2, достигая 5 у некоторых полупроводников[36]. В вакууме и диэлектрическая, и магнитная проницаемости равны единице:  .
.Поскольку уравнения Максвелла в линейной среде являются линейными относительно полей
 и свободных зарядов и токов
и свободных зарядов и токов  , справедлив принцип суперпозиции:
, справедлив принцип суперпозиции:Если распределения зарядов и токов
 создают электромагнитное поле с компонентами
создают электромагнитное поле с компонентами  , а другие распределения
, а другие распределения  создают, соответственно, поле
создают, соответственно, поле  , то суммарное поле, создаваемое источниками
, то суммарное поле, создаваемое источниками  , будет равно
, будет равно  .
.При распространении электромагнитных полей в линейной среде в отсутствие зарядов и токов сумма любых частных решений уравнений будет также удовлетворять уравнениям Максвелла.
Граничные условия
Во многих случаях неоднородную среду можно представить в виде совокупности кусочно-непрерывных однородных областей, разделённых бесконечно тонкими границами. При этом можно решать уравнения Максвелла в каждой области, «сшивая» на границах получающиеся решения. В частности, при рассмотрении решения в конечном объёме необходимо учитывать условия на границах объёма с окружающим бесконечным пространством. Граничные условия получаются из уравнений Максвелла предельным переходом. Для этого проще всего воспользоваться уравнениями Максвелла в интегральной форме.
Выбирая во второй паре уравнений контур интегрирования в виде прямоугольной рамки бесконечно малой высоты, пересекающей границу раздела двух сред, можно получить следующую связь между компонентами поля в двух областях, примыкающих к границе[37]:
СГС СИ  ,
, ,
,
 ,
, ,
,
где
 — единичный вектор нормали к поверхности, направленный из среды 1 в среду 2 и имеющий размерность, обратную длине,
— единичный вектор нормали к поверхности, направленный из среды 1 в среду 2 и имеющий размерность, обратную длине,  — плотность поверхностных свободных токов вдоль границы (то есть не включая связанных токов намагничивания, складывающихся на границе среды из микроскопических молекулярных итп токов). Первое граничное условие можно интерпретировать как непрерывность на границе областей тангенциальных компонент напряжённостей электрического поля (из второго следует, что тангенциальные компоненты напряжённости магнитного поля непрерывны только при отсутствии поверхностных токов на границе).
— плотность поверхностных свободных токов вдоль границы (то есть не включая связанных токов намагничивания, складывающихся на границе среды из микроскопических молекулярных итп токов). Первое граничное условие можно интерпретировать как непрерывность на границе областей тангенциальных компонент напряжённостей электрического поля (из второго следует, что тангенциальные компоненты напряжённости магнитного поля непрерывны только при отсутствии поверхностных токов на границе).Аналогичным образом, выбирая область интегрирования в первой паре интегральных уравнений в виде цилиндра бесконечно малой высоты, пересекающего границу раздела так, что его образующие перпендикулярны границе раздела, можно получить:
СГС СИ  ,
, ,
,
 ,
, ,
,
где
 — поверхностная плотность свободных зарядов (то есть не включающая в себя связанных зарядов, возникающих на границе среды вследствие диэлектрической поляризации самой среды).
— поверхностная плотность свободных зарядов (то есть не включающая в себя связанных зарядов, возникающих на границе среды вследствие диэлектрической поляризации самой среды).Эти граничные условия показывают непрерывность нормальной компоненты вектора магнитной индукции (нормальная компонента электрической индукции непрерывна только при отсутствии на границе поверхностных зарядов).
Из уравнения непрерывности можно получить граничное условие для токов:
 ,
,Важным частным случаем является граница раздела диэлектрика и идеального проводника. Поскольку идеальный проводник имеет бесконечную проводимость, электрическое поле внутри него равно нулю (иначе оно порождало бы бесконечную плотность тока). Тогда в общем случае переменных полей из уравнений Максвелла следует, что и магнитное поле в проводнике равно нулю. В результате тангенциальная компонента электрического и нормальная магнитного поля на границе с идеальным проводником равны нулю:
СГС СИ  ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, ,
,
Законы сохранения
Уравнения Максвелла содержат в себе законы сохранения заряда и энергии электромагнитного поля.
Уравнение непрерывности
Источники полей (
 ) не могут быть заданы произвольным образом. Применяя операцию дивергенции к четвёртому уравнению (закон Ампера—Максвелла) и используя первое уравнение (закон Гаусса), можно получить уравнение непрерывности для зарядов и токов:
) не могут быть заданы произвольным образом. Применяя операцию дивергенции к четвёртому уравнению (закон Ампера—Максвелла) и используя первое уравнение (закон Гаусса), можно получить уравнение непрерывности для зарядов и токов: Вывод уравнения непрерывности
Вывод уравнения непрерывностиДивергенция от ротора равна нулю, поэтому для четвёртого уравнения Максвелла (Закон Ампера—Максвелла) в системе СИ имеем:
![0=\nabla\cdot[\nabla\times \mathbf{H}] = \nabla\cdot\mathbf{j}+\frac{\partial \nabla\cdot \mathbf{D}}{\partial t}= \nabla\cdot\mathbf{j} + \frac{\partial \rho}{\partial t},](53d65cccfe32bfddf2059fc4a5434126.png)
где в последнем равенстве подставлено первое уравнение (Закон Гаусса).
Это уравнение при помощи интегральной теоремы Остроградского—Гаусса можно записать в следующем виде:

В левой части уравнения находится полный ток, протекающий через замкнутую поверхность
 . В правой части — изменение со временем заряда, находящегося внутри объёма
. В правой части — изменение со временем заряда, находящегося внутри объёма  . Таким образом, изменение заряда внутри объёма возможно только при его притоке или оттоке через поверхность
. Таким образом, изменение заряда внутри объёма возможно только при его притоке или оттоке через поверхность  , ограничивающую объём.
, ограничивающую объём.Уравнение непрерывности, эквивалентное закону сохранения заряда, далеко выходит за пределы классической электродинамики, оставаясь справедливым и в квантовой теории. Поэтому это уравнение само по себе может быть положено в основу электромагнитной теории. Тогда, например, ток смещения (производная по времени электрического поля) должен обязательно присутствовать в законе Ампера.
Из уравнений Максвелла для роторов и уравнения непрерывности с точностью до произвольных функций, не зависящих от времени, следуют законы Гаусса для электрического и магнитного полей.
Закон сохранения энергии
Если умножить третье уравнение Максвелла в дифференциальной форме (закон Фарадея) скалярно на
 , а четвёртое (закон Ампера — Максвелла) на
, а четвёртое (закон Ампера — Максвелла) на  и сложить результаты, можно получить теорему Пойнтинга:
и сложить результаты, можно получить теорему Пойнтинга:
где
СГС СИ Вывод теоремы ПойнтингаПри помощи третьего и четвёртого уравнения Максвелла в дифференциальной форме, в системе СИ можно получить:
![\mathbf{E}\cdot[\nabla\times\mathbf{H}] = \mathbf{E}\mathbf{j} + \mathbf{E}\cdot \frac{\partial \mathbf{D}}{\partial t},~~~~~~~~~~~~~
\mathbf{H}\cdot[\nabla\times\mathbf{E}] = -\mathbf{H}\cdot \frac{\partial \mathbf{B}}{\partial t}.](55f49c1540927fdad9f994212ace2fbb.png)
Разница левых частей уравнений сворачивается по следующей формуле векторного анализа (производная произведения):
![\nabla\cdot[\mathbf{E}\times\mathbf{H}]=\mathbf{H}\cdot[\nabla\times\mathbf{E}]-\mathbf{E}\cdot[\nabla\times\mathbf{H}].](672651485481d33d6b270d4148a02836.png)
В линейных, но, возможно, неизотропных средах, между напряжённостями и индукциями существует линейная связь. Например, для электрического поля
 . Если
. Если  симметричная матрица, не зависящая от времени, то:
симметричная матрица, не зависящая от времени, то:
Аналогично для магнитного поля.
Вектор
 называется вектором Пойнтинга (вектором плотности потока электромагнитной энергии) и определяет количество электромагнитной энергии, переносимой через единицу площади в единицу времени. Интеграл вектора Пойнтинга по сечению распространяющейся волны определяет её мощность. Важно отметить, что, как впервые указал Хевисайд, физический смысл потока энергии имеет только безвихревая часть вектора Пойнтинга. Вихревая часть, дивергенция которой равна нулю, не связана с переносом энергии. Заметим, что Хевисайд получил выражение для закона сохранения независимо от Пойнтинга. В русскоязычной литературе вектор Пойнтинга часто называется также «вектором Умова — Пойнтинга».
называется вектором Пойнтинга (вектором плотности потока электромагнитной энергии) и определяет количество электромагнитной энергии, переносимой через единицу площади в единицу времени. Интеграл вектора Пойнтинга по сечению распространяющейся волны определяет её мощность. Важно отметить, что, как впервые указал Хевисайд, физический смысл потока энергии имеет только безвихревая часть вектора Пойнтинга. Вихревая часть, дивергенция которой равна нулю, не связана с переносом энергии. Заметим, что Хевисайд получил выражение для закона сохранения независимо от Пойнтинга. В русскоязычной литературе вектор Пойнтинга часто называется также «вектором Умова — Пойнтинга».Величины
 и
и  определяют объёмные плотности энергии, соответственно, электрического и магнитного полей. При отсутствии токов и связанных с ними потерь теорема Пойнтинга является уравнением непрерывности для энергии электромагнитного поля. Проинтегрировав его в этом случае по некоторому замкнутому объёму и воспользовавшись теоремой Остроградского — Гаусса, можно получить закон сохранения энергии для электромагнитного поля:
определяют объёмные плотности энергии, соответственно, электрического и магнитного полей. При отсутствии токов и связанных с ними потерь теорема Пойнтинга является уравнением непрерывности для энергии электромагнитного поля. Проинтегрировав его в этом случае по некоторому замкнутому объёму и воспользовавшись теоремой Остроградского — Гаусса, можно получить закон сохранения энергии для электромагнитного поля:
Это уравнение показывает, что при отсутствии внутренних потерь изменение энергии электромагнитного поля в объёме происходит только за счёт мощности электромагнитного излучения, переносимого через границу этого объёма.
Вектор Пойнтинга связан с импульсом электромагнитного поля[38]:

где интегрирование производится по всему пространству. Электромагнитная волна, поглощаясь или отражаясь от некоторой поверхности, передаёт ей часть своего импульса, что проявляется в форме светового давления. Экспериментально этот эффект впервые наблюдался П. Н. Лебедевым в 1899 году.
Потенциалы
Скалярный и векторный потенциалы
Закон Фарадея и закон Гаусса для магнитной индукции выполняются тождественно, если электрическое и магнитное поля выразить через скалярный
 и векторный
и векторный  потенциалы[39]:
потенциалы[39]:СГС СИ ДоказательствоЕсли магнитное поле равно ротору векторного потенциала, то дивергенция автоматически равна нулю:
![\nabla\cdot\mathbf{B}= \nabla\cdot[\nabla\times\mathbf{A}]=[\nabla\times\nabla]\cdot\mathbf{A} = 0.](51b88b1c31e513eda276867f4a03870c.png)
Подставляя выражение для напряжённости электрического поля в закон Фарадея, например, в системе СИ, получаем:

При данных электрическом
 и магнитном
и магнитном  полях, скалярный и векторный потенциалы определены неоднозначно. Если
полях, скалярный и векторный потенциалы определены неоднозначно. Если  — произвольная функция координат и времени, то следующее преобразование не изменит значение полей:
— произвольная функция координат и времени, то следующее преобразование не изменит значение полей:СГС СИ Подобные преобразования играют важную роль в квантовой электродинамике и лежат в основе локальной калибровочной симметрии электромагнитного взаимодействия. Локальная калибровочная симметрия вводит зависимость от координат и времени в фазу глобальной калибровочной симметрии, которая, в силу теоремы Нётер, приводит к закону сохранения заряда.
Неоднозначность определения потенциалов оказывается удобной для наложения на них дополнительных условий, называемых калибровкой. Благодаря этому, уравнения электродинамики принимают более простой вид. Рассмотрим, например, уравнения Максвелла в однородных и изотропных средах с диэлектрической (
 ) и магнитной (
) и магнитной ( ) проницаемостями. Для данных
) проницаемостями. Для данных  и
и  всегда можно подобрать такую функцию
всегда можно подобрать такую функцию  , чтобы выполнялось калибровочное условие Лоренца[40]:
, чтобы выполнялось калибровочное условие Лоренца[40]:СГС СИ В этом случае оставшиеся уравнения Максвелла в однородных и изотропных средах могут быть записаны в следующем виде:
СГС СИ где
 — оператор Д’Аламбера, который и в системе СГС, и в системе СИ имеет вид:
— оператор Д’Аламбера, который и в системе СГС, и в системе СИ имеет вид:
Таким образом, 8 уравнений Максвелла для компонент электромагнитного поля (2 векторных и 2 скалярных) при помощи потенциалов могут быть сведены к 4 уравнениям (скалярному для
 и векторному для
и векторному для  ). Решения этих уравнений для произвольно двигающегося точечного заряда называются потенциалами Лиенара — Вихерта[41].
). Решения этих уравнений для произвольно двигающегося точечного заряда называются потенциалами Лиенара — Вихерта[41].Возможно введение других калибровок. Так, для решения ряда задач удобной оказывается кулоновская калибровка:

В этом случае:
СГС СИ ,
где
 — соленоидальная часть тока (
— соленоидальная часть тока ( ).
).Первое уравнение описывает мгновенное (без запаздывания) действие кулоновской силы, поскольку кулоновская калибровка неинвариантна относительно преобразований Лоренца. При этом энергию кулоновского взаимодействия можно отделить от остальных взаимодействий, что облегчает квантование поля в гамильтоновом формализме[42].
Векторный потенциал играет большую роль в электродинамике и в квантовой теории поля, однако для исследования процессов распространения электромагнитных волн в отсутствие токов и зарядов его введение часто не приводит к упрощению системы, а сводится к простой замене векторов электрического и магнитного поля на другой аналогичный вектор, описываемый теми же уравнениями. Так, для гармонических полей векторный потенциал будет просто пропорционален электрическому полю (скалярный потенциал при этом можно положить равным нулю).
Векторы Герца
- В 1887 году Генрих Герц предложил вместо непосредственного решения уравнений Максвелла для двух векторных функций электрического и магнитного полей или скалярного и векторного потенциалов перейти к новой единственной векторной функции, которая носит теперь имя электрического вектора Герца
 и позволяет в некоторых случаях упростить решение электродинамических задач, сводя их к решению скалярного волнового уравнения.
и позволяет в некоторых случаях упростить решение электродинамических задач, сводя их к решению скалярного волнового уравнения.
СГС СИ Заметим, что скалярный
 и векторный
и векторный  потенциалы, выраженные через вектор Герца, автоматически удовлетворяют калибровочному условию Лоренца. Вектор Герца учитывает все поля, связанные со свободными зарядами и их токами.
потенциалы, выраженные через вектор Герца, автоматически удовлетворяют калибровочному условию Лоренца. Вектор Герца учитывает все поля, связанные со свободными зарядами и их токами.Подставляя выражения для полей через электрический вектор в два последних уравнения Максвелла, можно получить[43][44]:
СГС СИ Здесь введён вектор поляризации свободных зарядов и токов:

(при этом уравнение непрерывности для заряда автоматически выполняется).
Таким образом, электрический вектор Герца определяется волновыми уравнениями, в правой части которых стоит поляризуемость, обусловленная свободными, либо свободными и связанными зарядами, то есть электрическими дипольными моментами.
- В 1901 году парный электрическому вектору Герца магнитный вектор, который также традиционно называют именем Герца, ввёл итальянский физик Аугусто Риги[45].
СГС СИ Поскольку поля, описываемые магнитным вектором Герца, не зависят от свободных зарядов и токов, а магнитные монополи не обнаружены, потенциалы удовлетворяют калибровке Лоренца в вырожденном виде — так называемой кулоновской калибровке (
 ,
,  ).
).Аналогичным образом можно получить уравнения для магнитного потенциала Герца, подставляя выраженные через него поля в третье и четвёртое уравнения Максвелла без тока:
СГС СИ Действие сторонних магнитных полей, связанных с внешними источниками, может быть учтено по аналогии с электрическим вектором Герца введением в правые части дополнительной магнитной поляризации
 .
.Таким образом, выделяется два типа электромагнитных полей, выражающихся через электрический и магнитный потенциалы Герца, а произвольное поле можно представить в виде суммы таких полей. Поля, выражающиеся через электрический вектор Герца носят название полей электрического типа или поперечно-магнитных (TM) полей, поскольку магнитное поле для них ортогонально направлению вектора Герца. Соответственно, поля, выражающиеся через магнитный вектор Герца, называют полями магнитного типа или поперечно-электрическими полями (TE), электрическое поле в которых ортогонально порождающему вектору Герца. Поля TM можно представить как поля, порождаемые распределёнными в пространстве электрическими диполями, а поля TE, соответственно, магнитными. Векторные потенциалы Герца, в свою очередь, могут быть во многих случаях выражены через скалярные потенциалы.
Потенциалы Дебая
В электродинамике широко используются скалярные потенциалы, предложенные Дебаем[46].
Волновое уравнение представляет собой систему трёх связанных скалярных уравнений, которые распадаются на три скалярных уравнения Гельмгольца только в декартовой системе координат. Для удобства поиска решений, удовлетворяющих граничным условиям желательно выбирать координатные системы, координатные поверхности которых близки или совпадают с поверхностями границ. Один из подходов к решению векторного уравнения Гельмгольца состоит во введении скалярных функций
 , удовлетворяющих скалярному волновому уравнению Гельмгольца, через которые затем могут быть выражены векторные поля[47]:
, удовлетворяющих скалярному волновому уравнению Гельмгольца, через которые затем могут быть выражены векторные поля[47]:Здесь
 — некоторая векторная функция координат. Вектор
— некоторая векторная функция координат. Вектор  , описывает потенциальную часть поля и его можно положить равным нулю при отсутствии свободных зарядов.
, описывает потенциальную часть поля и его можно положить равным нулю при отсутствии свободных зарядов.Если для некоторой ортогональной координатной системы существует функция
 , пропорциональная координатному вектору, то произвольное векторное поле, удовлетворяющее векторному уравнению Гельмгольца в этой системе, можно представить в виде суммы векторных функций, пропорциональных векторам
, пропорциональная координатному вектору, то произвольное векторное поле, удовлетворяющее векторному уравнению Гельмгольца в этой системе, можно представить в виде суммы векторных функций, пропорциональных векторам  и
и  . Как следует из уравнений Максвелла, электрическому полю, пропорциональному
. Как следует из уравнений Максвелла, электрическому полю, пропорциональному  , соответствует магнитное поле типа
, соответствует магнитное поле типа  и наоборот. При этом векторные потенциалы
и наоборот. При этом векторные потенциалы  соответствуют векторам Герца. Поскольку в этом случае поле, пропорциональное
соответствуют векторам Герца. Поскольку в этом случае поле, пропорциональное  , нормально вектору
, нормально вектору  , его компоненты являются тангенциальными к соответствующей
, его компоненты являются тангенциальными к соответствующей  координатной поверхности. Если границы в решаемой задаче совпадают с одной из таких координатных поверхностей, то удовлетворение граничным условиям существенно упрощается.
координатной поверхности. Если границы в решаемой задаче совпадают с одной из таких координатных поверхностей, то удовлетворение граничным условиям существенно упрощается.Такое представление возможно только в ограниченном числе ортогональных координатных систем[48]. В декартовой системе координат в качестве вектора
 может выступать любой координатный вектор. Соответствующие решения представляют собой плоские волны. Для цилиндрической системы координат
может выступать любой координатный вектор. Соответствующие решения представляют собой плоские волны. Для цилиндрической системы координат  , для сферической
, для сферической  . Кроме того, такое представление возможно в конической, а также относительно оси
. Кроме того, такое представление возможно в конической, а также относительно оси  в параболической и эллиптической цилиндрических системах координат.
в параболической и эллиптической цилиндрических системах координат.Векторы Римана — Зильберштейна
Если ввести комплексный вектор Римана — Зильберштейна
 и комплексно сопряжённый ему вектор
и комплексно сопряжённый ему вектор  [49][50][51]:
[49][50][51]:СГС СИ то уравнения Максвелла сводятся к двум:
СГС СИ При отсутствии сторонних зарядов и токов остаётся только второе уравнение (первое из-за равенства дивергенции ротора нулю в этом случае удовлетворяется автоматически с точностью до не зависящей от времени компоненты):

В отличие от волнового уравнения, которое получаются в этом случае для векторов поля или потенциала, последнее векторное дифференциальное уравнение имеет первый, а не второй порядок и поэтому в ряде случаев может быть проще для решения.
Для гармонического поля с зависимостью
 вектор
вектор  является собственным вектором оператора ротора:
является собственным вектором оператора ротора:
При выбранной нормировке
 имеет смысл комплексной амплитуды электромагнитного поля, а его квадрат модуля
имеет смысл комплексной амплитуды электромагнитного поля, а его квадрат модуля
имеет смысл плотности энергии поля.

Векторы
 и
и  можно интерпретировать как волновые функции циркулярно поляризованных фотонов[50].
можно интерпретировать как волновые функции циркулярно поляризованных фотонов[50].Ковариантная формулировка
С современной точки зрения, четырёхмерная ковариантная формулировка электродинамики, и в частности — запись уравнений Максвелла в таком виде, является физически наиболее фундаментальной.
Практически она приводит, кроме явной ковариантности, к значительно большей компактности уравнений, а значит определенной красоте и в ряде случаев удобству, и более органично и прямо включает в себя единство электромагнитного поля.
Под ковариантной формулировкой понимают два различающихся, но прямо и непосредственно связанных варианта: лоренц-ковариантная формулировка в плоском пространстве-времени Минковского и общековариантная формулировка для общего случая искривленного пространства-времени (стандартно рассматриваемая в контексте общей теории относительности). Второй вариант отличается от первого тем, что метрика пространства-времени в нём не постоянна (что может означать как присутствие гравитации, так и просто использование более широкого класса координат, например, соответствующих неинерциальным системам отсчёта), и во многом сводится к замене обычных производных по (четырехмерным) координатам на ковариантные производные (в значительной части случаев это сводится к механической замене первых на вторые). Кроме прочего, второй вариант позволяет исследовать взаимодействие электромагнитного поля с гравитацией.
- Ниже сначала рассмотрен (как более простой) первый вариант — вариант лоренц-ковариантной формулировки в плоском пространстве-времени.
Четырёхмерные векторы
При ковариантной записи уравнений электродинамики производится переход от трёхмерных векторов и скаляров к четырёхмерным векторам (4-векторы). Независимо от системы единиц, четырехмерные координаты (4-вектор координат, в компоненты которого входят время и трехмерные пространственные координаты), производная по этим координатам (4-производная) и плотность тока определяются следующим образом[52]:



Индекс 4-вектора принимает значения
 . В компонентной записи вектора сначала идёт нулевая компонента, затем — пространственные. Например, время равно
. В компонентной записи вектора сначала идёт нулевая компонента, затем — пространственные. Например, время равно  , а плотность заряда
, а плотность заряда  . В силу этих определений, закон сохранения заряда в ковариантной форме принимает следующий вид:
. В силу этих определений, закон сохранения заряда в ковариантной форме принимает следующий вид:
По повторяющемуся индексу предполагается суммирование от 0 до 3 (правило Эйнштейна).
ПримерПриведенное выше уравнение является компактной записью уравнения непрерывности:

Введём 4-вектор потенциала, имеющий в системах СГС и СИ следующие компоненты:
СГС СИ При ковариантной записи играет роль положение индекса у 4-вектора. Если индекс находится внизу, то такой вектор называется ковариантным вектором (или ковектором), и его пространственные компоненты имеют обратный знак по сравнению с компонентами 4-вектора. Поднятие и опускание индексов проводится при помощи метрического тензора
 , который в четырёхмерном пространстве Минковского имеет диагональный вид с сигнатурой:
, который в четырёхмерном пространстве Минковского имеет диагональный вид с сигнатурой:  .
.При помощи такого определения 4-вектора потенциала, калибровочное условие Лоренца в ковариантной форме можно записать следующим образом:

Если это условие выполняется, то уравнения Максвелла для потенциалов в вакууме при наличии зарядов и токов принимают вид:
СГС СИ  ,
,
где
 — оператор Даламбера с обратным знаком:
— оператор Даламбера с обратным знаком:
Нулевая компонента уравнений Максвелла для 4-вектора потенциала соответствует уравнению для
 , а пространственная — для
, а пространственная — для  .
.Тензор электромагнитного поля
Определим ковариантный тензор электромагнитного поля при помощи производной от 4-вектора потенциала[53][54]:

Явный вид этого антисимметричного тензора (
 ) может быть представлен в следующем виде:
) может быть представлен в следующем виде:СГС СИ Временные компоненты тензора составлены из компонент напряжённости электрического поля, а пространственные — магнитного, что может быть записано следующим образом:
 . В тензоре электромагнитного поля с верхними индексами изменяется знак у нулевых компонент (то есть перед компонентами электрического поля):
. В тензоре электромагнитного поля с верхними индексами изменяется знак у нулевых компонент (то есть перед компонентами электрического поля):  .
.Используя определение тензора электромагнитного поля, несложно проверить выполнение следующего тождества:

Его можно переписать в более компактном виде, введя дуальный тензор электромагнитного поля:

где
 — антисимметричный символ Леви-Чивиты (
— антисимметричный символ Леви-Чивиты ( ). Это уравнение является ковариантной записью закона Гаусса для магнитного поля и закона электромагнитной индукции Фарадея. Компоненты дуального тензора
). Это уравнение является ковариантной записью закона Гаусса для магнитного поля и закона электромагнитной индукции Фарадея. Компоненты дуального тензора  получаются из тензора
получаются из тензора  в результате перестановки электрического и магнитного полей[55]:
в результате перестановки электрического и магнитного полей[55]:  ,
,  .
.Полная система уравнений Максвелла в ковариантной форме имеет вид:
СГС СИ По повторяющемуся индексу
 проводится суммирование от 0 до 3, а в правой части второго уравнения находится 4-вектор тока. Нулевая компонента этого уравнения соответствует закону Гаусса, а пространственные — закону Ампера — Максвелла.
проводится суммирование от 0 до 3, а в правой части второго уравнения находится 4-вектор тока. Нулевая компонента этого уравнения соответствует закону Гаусса, а пространственные — закону Ампера — Максвелла.При помощи тензора электромагнитного поля можно получить законы преобразований компонент электрического и магнитного полей, измеряемых относительно различных инерциальных систем отсчёта[56][57]:
СГС СИ где «штрихованные» величины измеряются относительно системы отсчёта, движущейся вдоль оси
 со скоростью
со скоростью  относительно системы, в которой измеряются «не штрихованные» компоненты полей, а
относительно системы, в которой измеряются «не штрихованные» компоненты полей, а  — фактор Лоренца. Компоненты полей вдоль направления относительного движения инерциальных систем отсчёта остаются неизменными:
— фактор Лоренца. Компоненты полей вдоль направления относительного движения инерциальных систем отсчёта остаются неизменными:  .
.Уравнения Максвелла в вакууме инвариантны относительно преобразований Лоренца. Это послужило одним из толчков к созданию специальной теории относительности.
Электрическое и магнитное поля различным образом изменяются при инверсии осей пространственной системы координат. Электрическое поле является полярным вектором, а магнитное — аксиальным вектором. Можно построить две инвариантные относительно преобразований Лоренца величины:

Первый инвариант является скаляром, а второй — псевдоскаляром, то есть изменяет свой знак при инверсии координатных осей.
Лагранжиан
Действие
 и лагранжиан (функция Лагранжа)
и лагранжиан (функция Лагранжа)  для пробного заряда, двигающегося во внешнем электромагнитном поле в системе СГС и СИ имеют вид [58] [59]:
для пробного заряда, двигающегося во внешнем электромагнитном поле в системе СГС и СИ имеют вид [58] [59]:СГС СИ где:
 — масса частицы (в единицах СИ — кг);
— масса частицы (в единицах СИ — кг); — её скорость (в единицах СИ — м/с);
— её скорость (в единицах СИ — м/с); — заряд частицы (в единицах СИ — Кл);
— заряд частицы (в единицах СИ — Кл); — 4-х интервал.
— 4-х интервал.
Уравнения движения заряда под воздействием силы Лоренца в ковариантной записи имеют вид:
СГС СИ Уравнения Максвелла получаются из принципа наименьшего действия, в котором динамическими переменными являются 4-х потенциалы электромагнитного поля
 . При этом используется следующее ковариантное выражение для действия[59][60]:
. При этом используется следующее ковариантное выражение для действия[59][60]:СГС СИ где производится интегрирование по инвариантному 4-объёму
 .
.Запись при помощи дифференциальных форм
Уравнения Максвелла в ковариантной форме, аналогично векторному представлению в трёхмерном пространстве, можно записать в «безындексной форме». Для этого вводится операция внешнего произведения
 , обладающая свойством антисимметричности
, обладающая свойством антисимметричности  . Внешнее произведение позволяет записывать свёрнутые по всем индексам выражения с антисимметричными тензорами, такими как
. Внешнее произведение позволяет записывать свёрнутые по всем индексам выражения с антисимметричными тензорами, такими как  . При этом возникают объекты, называемые дифференциальными формами (или просто формами)[61]. 1-форма потенциала поля определяется следующим образом (по индексу
. При этом возникают объекты, называемые дифференциальными формами (или просто формами)[61]. 1-форма потенциала поля определяется следующим образом (по индексу  — сумма от 0 до 3):
— сумма от 0 до 3):
Из 1-формы, при помощи операции внешнего дифференцирования
 , получается 2-форма электромагнитного поля (или 2-форма Фарадея):
, получается 2-форма электромагнитного поля (или 2-форма Фарадея):
Операция внешнего дифференцирования обладает свойством
 , что приводит к закону Гаусса для магнитного поля и закону Фарадея:
, что приводит к закону Гаусса для магнитного поля и закону Фарадея:
Для записи оставшихся уравнений Максвелла вводится дуальная к
 2-форма
2-форма  , называемая также 2-формой Максвелла[62]:
, называемая также 2-формой Максвелла[62]:
и 3-форма тока:

где
 — абсолютный антисимметричный символ Леви-Чивиты (
— абсолютный антисимметричный символ Леви-Чивиты ( ). Свёртка с символом Леви-Чевиты внешнего произведения дифференциалов называется оператором звезды Ходжа.
). Свёртка с символом Леви-Чевиты внешнего произведения дифференциалов называется оператором звезды Ходжа.В этих обозначениях уравнения Максвелла в системах СГС и СИ принимают следующий вид[63]:
СГС СИ ДоказательствоЧтобы показать эквивалентность этих уравнений уравнениям Максвелла, необходимо записать их в трёхмерной векторной форме. В этом случае, в системе СГС, ток и 2-форма Максвелла имеют вид:

где
 - трёхмерный объём, а
- трёхмерный объём, а  - вектор площади поверхности в трёхмерном пространстве. Так как:
- вектор площади поверхности в трёхмерном пространстве. Так как:
то, с учётом уравнений Максвелла в дифференциальной форме, получим
 .
.С учётом тождества
 , последнее уравнение Максвелла, записанное при помощи дифференциальных форм сразу приводит к уравнению непрерывности (закону сохранения заряда):
, последнее уравнение Максвелла, записанное при помощи дифференциальных форм сразу приводит к уравнению непрерывности (закону сохранения заряда):
В такой форме уравнения Максвелла остаются справедливыми и на произвольном 4-мерном многообразии, например, в искривлённом пространстве-времени общей теории относительности. В этом случае, в соотношениях дополнительно появляется определитель метрического тензора
 . Например, для тока и внешнего дифференцирования:
. Например, для тока и внешнего дифференцирования:
Общековариантная запись в компонентах
На произвольном 4-мерном многообразии, то есть в общем случае, включающем и пространство-время ненулевой кривизны (а также произвольных четырехмерных координат, включая случаи неинерциальных систем отсчета) электродинамика может быть сформулирована и в обычных индексных обозначениях.
В основном рецепт перехода от случая нулевой кривизны пространства-времени и лоренцевых систем отсчета в нем, подробно описанного выше, к общему случаю состоит в замене обычных производных по координатам на ковариантные производные, учёт того, что метрика в этом случае не постоянна и не имеет специального лоренцева вида (то есть практически произвольна), а также при интегрировании — например, при записи действия — учёт того, что метрика входит в элемент объема (через множитель
 — корень из минус детерминанта метрики).
— корень из минус детерминанта метрики).Спектральное представление
В электродинамике большое значение имеют гармонические колебания. Такие поля можно представить в виде:
![\mathbf{E}(\mathbf{r},t)=\frac{1}{2}\left[\tilde{\mathbf{E}}(\mathbf{r})e^{-i\omega t}+ \mbox{c. c.}\right]=\Re[\tilde{\mathbf{E}}(\mathbf{r})e^{-i\omega t}],](a9c748094a46d19e7a0b6373ecc3dab2.png)
![\mathbf{H}(\mathbf{r},t)=\frac{1}{2}\left[\tilde{\mathbf{H}}(\mathbf{r})e^{-i\omega t}+\mbox{c. c.}\right]=\Re[\tilde{\mathbf{H}}(\mathbf{r})e^{-i\omega t}].](0bda7a7ff5d7ed9ad1ff12ce7f2d8b53.png)
где
 — частота колебаний поля. Обозначение «c. c.» означает комплексное сопряжение предыдущего слагаемого. В некоторых работах коэффициент 1/2 в соглашении о гармонических амплитудах не используется, что приводит к соответствующей модификации всех связанных с этим соглашением выражений. В литературе также часто встречается выбор обратного знака в комплексной экспоненте. Рассмотренный здесь вариант согласуется с принятым в квантовой теории в представлении Шрёдингера.
— частота колебаний поля. Обозначение «c. c.» означает комплексное сопряжение предыдущего слагаемого. В некоторых работах коэффициент 1/2 в соглашении о гармонических амплитудах не используется, что приводит к соответствующей модификации всех связанных с этим соглашением выражений. В литературе также часто встречается выбор обратного знака в комплексной экспоненте. Рассмотренный здесь вариант согласуется с принятым в квантовой теории в представлении Шрёдингера.Усреднённые за период плотности энергии электрического и магнитного поля равны, соответственно:
СГС СИ Используя преобразование Фурье, по гармоническим колебаниям можно разложить поля с произвольной временной зависимостью.
Переход к спектральным компонентам позволяет сосредоточиться на координатной зависимости полей. Уравнения Максвелла для спектральных компонент в однородных средах при этом принимают вид:
СГС СИ Диэлектрическая и магнитная проницаемости среды в спектральном представлении связаны с восприимчивостями материальных уравнений в интегральном представлении Фурье-преобразованием:
СГС СИ Уравнения без свободных зарядов и токов
В отсутствие свободных зарядов и токов
 ,
,  , в изотропных и однородных средах без дисперсии уравнения Максвелла принимают следующий вид:
, в изотропных и однородных средах без дисперсии уравнения Максвелла принимают следующий вид:СГС СИ Решениями этих уравнений является напряжённость электрического поля
 и магнитная индукция
и магнитная индукция  . Диэлектрическая
. Диэлектрическая  и магнитная
и магнитная  проницаемости определяются свойствами среды. Для вакуума
проницаемости определяются свойствами среды. Для вакуума  ,
,  .
.Волновое уравнение
Уравнения Максвелла являются дифференциальными уравнениями первого порядка по координатам и времени. Однако, во второй паре в каждое уравнение входят обе неизвестные векторные функции
 и
и  . При отсутствии зарядов и токов можно перейти к уравнениям второго порядка, каждое из которых зависит только от одного, электрического или магнитного поля:
. При отсутствии зарядов и токов можно перейти к уравнениям второго порядка, каждое из которых зависит только от одного, электрического или магнитного поля:
Такие уравнения называются волновыми.
Вывод волнового уравненияБеря ротор от закона Фарадея, и используя закон Ампера-Максвелла, получаем (в системе СИ):
С другой стороны, раскрывая двойное векторное произведение, имеем:
так как дивергенция электрического поля в вакууме равна нулю. Приравнивая эти два выражения, получаем волновое уравнение для электрического поля. Аналогично получается волновое уравнение для магнитного поля.
В лоренцевской калибровке в отсутствие зарядов и токов волновому уравнению удовлетворяют также векторный и скалярный потенциалы:

Величина
 , входящая в волновые уравнения определяет скорость распространения электромагнитных полей в среде. Её максимальное значение
, входящая в волновые уравнения определяет скорость распространения электромагнитных полей в среде. Её максимальное значение  достигается в вакууме, когда
достигается в вакууме, когда  и
и  .
.Уравнение Гельмгольца
Пусть
 — круговая частота гармонического сигнала и зависимость от времени выбрана в виде
— круговая частота гармонического сигнала и зависимость от времени выбрана в виде  . При отсутствии электрических зарядов в среде, уравнение Гельмгольца принимает вид:
. При отсутствии электрических зарядов в среде, уравнение Гельмгольца принимает вид:
где
 .
.Некоторые точные решения
Поле движущегося точечного заряда
Если заряд движется с постоянной скоростью
 , то вокруг него возникает магнитное поле
, то вокруг него возникает магнитное поле  , а напряжённость электрического перестаёт быть сферически симметричной [64]:
, а напряжённость электрического перестаёт быть сферически симметричной [64]:СГС СИ Единичный вектор
 направлен от заряда к точке измерения напряжённости поля.
направлен от заряда к точке измерения напряжённости поля.  — модуль вектора
— модуль вектора  . Если ввести угол
. Если ввести угол  между векторами
между векторами  и
и  , то
, то ![[\mathbf{n}\times\mathbf{u}]^2=u^2\sin^2\theta](678c14a1934c7427d96c692e74fbec78.png) . При фиксированном расстоянии от заряда напряжённость электрического поля минимальна в точках, находящихся на линии движения заряда. Максимальное значение достигается в плоскости, проходящей через заряд перпендикулярно его скорости. Магнитная индукция, в силу векторного произведения, перпендикулярна скорости и электрическому полю. Так как заряд движется, в фиксированной точке пространства электрическое и магнитное поля изменяются со временем. Они удовлетворяют уравнениям Максвелла с плотностью заряда и тока, пропорциональных дельта-функции Дирака:
. При фиксированном расстоянии от заряда напряжённость электрического поля минимальна в точках, находящихся на линии движения заряда. Максимальное значение достигается в плоскости, проходящей через заряд перпендикулярно его скорости. Магнитная индукция, в силу векторного произведения, перпендикулярна скорости и электрическому полю. Так как заряд движется, в фиксированной точке пространства электрическое и магнитное поля изменяются со временем. Они удовлетворяют уравнениям Максвелла с плотностью заряда и тока, пропорциональных дельта-функции Дирака:
где
 — текущее положение заряда.
— текущее положение заряда.На пробный заряд
 , двигающийся в той же системе отсчёта, действует сила Лоренца. Она может быть получена при помощи преобразований Лоренца из закона Кулона и принципа инвариантности заряда[65]. В этом смысле магнитное поле по своей природе является релятивистским эффектом.
, двигающийся в той же системе отсчёта, действует сила Лоренца. Она может быть получена при помощи преобразований Лоренца из закона Кулона и принципа инвариантности заряда[65]. В этом смысле магнитное поле по своей природе является релятивистским эффектом.Если точечный заряд двигается с ускорением, то создаваемое им поле зависит не только от скорости, но и от ускорения. Составляющая поля, зависящая от ускорения, соответствует излучению электромагнитной волны[41].
Плоские электромагнитные волны
- Предположим, что напряжённость электрического поля и магнитная индукция являются произвольными функциями следующей комбинации координат и времени:

где
 — некоторый постоянный вектор. В этом случае
— некоторый постоянный вектор. В этом случае  и
и  удовлетворяют уравнениям Максвелла в отсутствие зарядов и токов, если между ними существует следующая связь:
удовлетворяют уравнениям Максвелла в отсутствие зарядов и токов, если между ними существует следующая связь:СГС СИ и они перпендикулярны вектору
 , который должен быть единичным:
, который должен быть единичным: Вывод решения для плоской волны
Вывод решения для плоской волныЕсли напряжённость электрического поля зависит от координат и времени в виде следующей их комбинации
 , то для производной
, то для производной  -той компоненты вектора
-той компоненты вектора  по
по  -той координате и времени можно записать:
-той координате и времени можно записать:
и аналогично для магнитной индукции. Поэтому уравнения Максвелла в отсутствие зарядов и токов принимают вид (система СИ):
![\frac{d(\mathbf{n}\mathbf{E})}{du} = 0,~~~~~~~~
\frac{d(\mathbf{n}\mathbf{B})}{du} = 0,~~~~~~~~
\frac{d}{du}\bigl([\mathbf{n}\times \mathbf{E}] - \frac{c}{\sqrt{\varepsilon\mu}}\mathbf{B}\bigr)= 0,~~~~~~~~
\frac{d}{du}\bigl([\mathbf{n}\times \mathbf{B}] + \frac{\sqrt{\varepsilon\mu}}{c} \mathbf{E}\bigr)= 0.](505c1b1c80d7694672ef6738f43b4de3.png)
Интегрируя эти соотношения по
 и опуская константы интегрирования, которые соответствуют постоянным полям, получаем:
и опуская константы интегрирования, которые соответствуют постоянным полям, получаем:![\mathbf{n}\mathbf{E} = 0,~~~~~~~~~
\mathbf{n}\mathbf{B} = 0,~~~~~~~~~
\mathbf{B} = \frac{\sqrt{\varepsilon\mu}}{c}\,[\mathbf{n}\times \mathbf{E}],~~~~~~~~~
\mathbf{E}= -\frac{c}{\sqrt{\varepsilon\mu}}\, [\mathbf{n}\times \mathbf{B}].](c7bf7f7da0bd1298d6ca59b1c2ace292.png)
Подставляя четвёртое уравнение в третье, получаем
 .
.Физический смысл решения в виде плоской волны состоит в следующем. Выберем ось
 декартовой системы координат так, чтобы вектор
декартовой системы координат так, чтобы вектор  был направлен вдоль неё. Тогда электрические и магнитные поля волны зависят от координаты
был направлен вдоль неё. Тогда электрические и магнитные поля волны зависят от координаты  и времени
и времени  следующим образом:
следующим образом:
Предположим, что в начальный момент времени
 , напряжённость поля является произвольной векторной функцией
, напряжённость поля является произвольной векторной функцией  . С течением времени, эта функция будет сдвигаться в пространстве вдоль оси
. С течением времени, эта функция будет сдвигаться в пространстве вдоль оси  со скоростью
со скоростью  .
.В электромагнитной волне в общем случае напряжённость поля может быть произвольной непериодической функцией
 . Например, решение в виде плоской волны может описывать электромагнитный импульс локализованный вдоль направления движения. В плоскости перпендикулярной
. Например, решение в виде плоской волны может описывать электромагнитный импульс локализованный вдоль направления движения. В плоскости перпендикулярной  , электромагнитные поля не изменяются, что означает, что в этой плоскости плоская волна не ограничена и имеет плоский фазовый фронт (именно поэтому волна называется плоской). Так как электрическое и магнитное поля при распространении плоской волны всё время остаются перпендикулярными вектору
, электромагнитные поля не изменяются, что означает, что в этой плоскости плоская волна не ограничена и имеет плоский фазовый фронт (именно поэтому волна называется плоской). Так как электрическое и магнитное поля при распространении плоской волны всё время остаются перпендикулярными вектору  , такие волны называют «поперечными» или «трансверсальными». Векторы
, такие волны называют «поперечными» или «трансверсальными». Векторы  и
и  , в силу свойств векторного произведения, также перпендикулярны друг другу.
, в силу свойств векторного произведения, также перпендикулярны друг другу. Плотности энергии электрического и магнитного поля в плоской волне равны друг другу:
Плотности энергии электрического и магнитного поля в плоской волне равны друг другу:СГС СИ Вектор Пойнтинга (плотность потока энергии), независимо от системы единиц, связан с полной плотностью энергии следующим образом:

Это соотношение соответствует уравнению связи импульса и энергии для безмассовой частицы в релятивистской теории. Однако, скорость
 в среде меньше чем скорость света в вакууме
в среде меньше чем скорость света в вакууме  .
.Плоские и поперечные волны являются математическими абстракциями. Реальные волны конечной апертуры из-за эффекта дифракции можно считать плоскими и поперечными лишь в некотором приближении.
 Важный частный случай решения в виде плоских волн возникает, когда напряжённости полей являются гармоническими периодическими функциями. Выберем координатную ось
Важный частный случай решения в виде плоских волн возникает, когда напряжённости полей являются гармоническими периодическими функциями. Выберем координатную ось  вдоль волнового вектора
вдоль волнового вектора  . Тогда вектор электрического поля (как, впрочем, и магнитного) будет лежать в плоскости
. Тогда вектор электрического поля (как, впрочем, и магнитного) будет лежать в плоскости  , то есть
, то есть  . Если по каждой проекции в этой плоскости электрическое поле совершает периодические колебания, то такую волну называют монохроматической плоской волной:
. Если по каждой проекции в этой плоскости электрическое поле совершает периодические колебания, то такую волну называют монохроматической плоской волной:
Сравнение с общим решением для плоской волны, приводит к следующей связи между вектором
 и константой
и константой  , которое называется уравнением дисперсии:
, которое называется уравнением дисперсии:
В этом случае, вектор
 называется волновым вектором, а
называется волновым вектором, а  — круговой частотой монохроматической электромагнитной волны. Модуль волнового вектора и круговая частота связаны с длиной волны
— круговой частотой монохроматической электромагнитной волны. Модуль волнового вектора и круговая частота связаны с длиной волны  и её частотой
и её частотой  следующим образом:
следующим образом:
Константы
 и
и  являются сдвигами фазы, а
являются сдвигами фазы, а  и
и  — амплитудами колебаний вдоль каждой оси.
— амплитудами колебаний вдоль каждой оси.В фиксированной точке пространства (
 ) вектор электрического поля, в общем случае, описывает в плоскости
) вектор электрического поля, в общем случае, описывает в плоскости  эллипс, поэтому такие волны называются эллиптически поляризованными. Их частным случаем являются волны поляризованные по кругу. Вырожденный в прямую эллипс соответствует колебаниям напряжённости поля вдоль одной прямой в плоскости
эллипс, поэтому такие волны называются эллиптически поляризованными. Их частным случаем являются волны поляризованные по кругу. Вырожденный в прямую эллипс соответствует колебаниям напряжённости поля вдоль одной прямой в плоскости  . Такие волны называются линейно поляризованными. Аналогична ситуация с вектором магнитной индукции, который всё время перпендикулярен напряжённости электрического поля.
. Такие волны называются линейно поляризованными. Аналогична ситуация с вектором магнитной индукции, который всё время перпендикулярен напряжённости электрического поля.Связь с другими теориями
Уравнения Максвелла полностью совместимы с принципами специальной теории относительности. Они также применимы при микроскопическом описании вещества, когда заряженные частицы подчиняются принципам квантовой механики, а электромагнитное поле остаётся классическим (не квантовым). В этом случае квантовые объекты (например, электроны) описываются уравнением Шрёдингера или уравнением Дирака, однако, потенциалы электромагнитного взаимодействия в этих уравнениях определяются классическими уравнениями Максвелла.
Тем не менее, существуют явления, для описания которых требуется более последовательное объединение полевого подхода Фарадея — Максвелла с принципами квантовой механики. Оно осуществляется при помощи методов квантовой теории поля в квантовой электродинамике. В этом случае форма уравнений Максвелла (лагранжиан) остаётся неизменной, однако поля становятся операторами, а уравнения Максвелла — операторными уравнениями Гейзенберга. Решение подобных уравнений приводит к появлению новых эффектов, отсутствующих в классической теории поля. Эти эффекты существенны, в частности, в следующих физических ситуациях:
- Сверхсильные поля (
 ≈1.32×1018 В/м, где
≈1.32×1018 В/м, где  — масса электрона,
— масса электрона,  — его заряд,
— его заряд,  — постоянная Планка) — работа такого поля на комптоновской длине волны электрона равна по порядку величины энергии покоя электрона, что приводит к самопроизвольной генерации электрон-позитронных пар из вакуума (эффект Швингера)[66]. В результате возникает эффективное взаимодействие фотонов, которое отсутствует в классической электродинамике, приводящее к эффективному изменению лагранжиана поля (например, в низкоэнергетическом пределе поле описывается лагранжианом Гейзенберга — Эйлера[67]).
— постоянная Планка) — работа такого поля на комптоновской длине волны электрона равна по порядку величины энергии покоя электрона, что приводит к самопроизвольной генерации электрон-позитронных пар из вакуума (эффект Швингера)[66]. В результате возникает эффективное взаимодействие фотонов, которое отсутствует в классической электродинамике, приводящее к эффективному изменению лагранжиана поля (например, в низкоэнергетическом пределе поле описывается лагранжианом Гейзенберга — Эйлера[67]). - Сверхслабые поля, с энергией
 , где
, где  — частота поля (см. формула Планка). В этом случае становятся заметными отдельные кванты электромагнитного поля — фотоны.
— частота поля (см. формула Планка). В этом случае становятся заметными отдельные кванты электромагнитного поля — фотоны. - Для описания эффектов поглощения и испускания света атомами и молекулами.
- Для описания неклассических, например, сжатых состояний поля[68].
- На малых расстояниях, сравнимых с комптоновской длиной волны электрона,
 ≈ 3,86×10−13 м, когда в результате вакуумных эффектов, модифицируется, например, закон Кулона.
≈ 3,86×10−13 м, когда в результате вакуумных эффектов, модифицируется, например, закон Кулона.
Аксиоматический подход
Исторически уравнения Максвелла возникли в результате обобщения различных экспериментальных открытий. Однако с аксиоматической точки зрения их можно получить при помощи следующей последовательности шагов[69]:
- Постулируются:
- закон Кулона (сила
 , действующая на пробный заряд
, действующая на пробный заряд  со стороны неподвижного заряда
со стороны неподвижного заряда  );
); - инвариантность заряда в различных инерциальных системах отсчёта;
- принцип суперпозиции.
- закон Кулона (сила
- При помощи преобразований Лоренца получается значение для вектора силы
 , действующей на пробный заряд, со стороны равномерно двигающегося со скоростью
, действующей на пробный заряд, со стороны равномерно двигающегося со скоростью  заряда
заряда  , которое совпадает с силой Лоренца.
, которое совпадает с силой Лоренца. - Дивергенция и ротор, вычисленные от электрической (
 ) и магнитной (
) и магнитной ( ) составляющих силы дают уравнения Максвелла для точечного заряда. В силу принципа суперпозиции они записываются для произвольного распределения зарядов и токов. В заключение постулируется применимость этих уравнений и к ускоренному движению зарядов.
) составляющих силы дают уравнения Максвелла для точечного заряда. В силу принципа суперпозиции они записываются для произвольного распределения зарядов и токов. В заключение постулируется применимость этих уравнений и к ускоренному движению зарядов.
Второй подход основан на лагранжевом формализме [70]. При этом постулируется, что электромагнитное поле описывается линейным взаимодействием четырёхмерного потенциала
 , с четырёх-вектором электрического тока
, с четырёх-вектором электрического тока  , а свободный лагранжиан пропорционален инвариантной свёртке квадрата тензора электромагнитного поля
, а свободный лагранжиан пропорционален инвариантной свёртке квадрата тензора электромагнитного поля  .
.Как в первом, так и во втором подходе предполагаются установленными принципы теории относительности. Хотя исторически она возникла на основе уравнений Максвелла и второго постулата Эйнштейна, известен, восходящий к работам Игнатовского [71], Франка и Роте [72], аксиоматический способ построения СТО, не использующий постулата об инвариантности скорости света и уравнений Максвелла.
В обоих аксиоматических подходах получаются уравнения Максвелла в вакууме при наличии свободных зарядов. Расширение этих уравнений на электродинамику сплошных сред требует дальнейшего привлечения различных модельных представлений о структуре вещества.
Единственность решений уравнений Максвелла
Уравнения Максвелла являются дифференциальными уравнениями в частных производных. Поэтому для их решения необходимо задать начальные и граничные условия. При фиксированных функциях плотности заряда и тока для нестационарных полей получаемое решение единственно. Этот факт формулируется в виде теоремы[73][74][75]:
Если напряженности электрического и магнитного полей заданы в начальный момент времени
 в каждой точке некоторой области пространства
в каждой точке некоторой области пространства  и в течениe всего времени
и в течениe всего времени  заданы тангенциальные (касательные) составляющие напряженности электрического или магнитного поля на границе этой области
заданы тангенциальные (касательные) составляющие напряженности электрического или магнитного поля на границе этой области  , то существует единственное решение уравнений Максвелла.Доказательство
, то существует единственное решение уравнений Максвелла.ДоказательствоПусть электрическая и магнитная индукции связаны с напряжённостями полей при помощи следующих материальных уравнений:

где
 и
и  - положительно определённые, симметричные, стационарные матрицы. Если при данных начальных и граничных условиях существуют два различных решения, то следующие величины будут отличны от нуля:
- положительно определённые, симметричные, стационарные матрицы. Если при данных начальных и граничных условиях существуют два различных решения, то следующие величины будут отличны от нуля:
где индекс указывает номер решения. Так как начальные и граничные условия заданы (одинаковые для обоих возможных решений), то:
![\mathbf{e}(\mathbf{r}, 0)=\mathbf{h}(\mathbf{r}, 0)=0,~~~~~~~~~~~~~~~
[\mathbf{e}_\tau(\mathbf{r}, t) \cup \mathbf{h}_\tau(\mathbf{r}, t)]\Big|_s=0.](762c5c01944cb1fa1a7147d6f47b1fad.png)
Первые соотношения соответствуют начальным условиям, в вторые - граничным условиям на поверхности
 , где
, где  . (Индекс
. (Индекс  - нормальная составляющая к поверхности, а
- нормальная составляющая к поверхности, а  - касательная. Аналогично для
- касательная. Аналогично для  ) Подстановка функций
) Подстановка функций  и
и  в уравнения Максвелла для роторов приводит к следующим уравнениям:
в уравнения Максвелла для роторов приводит к следующим уравнениям:
где коэффициент
 равен
равен  в системе СГС и единице в системе СИ. Если одно из разностных полей
в системе СГС и единице в системе СИ. Если одно из разностных полей  или
или  равно нулю, то в силу нулевых начальных условий, соответственно, из первого или второго уравнения следует равенство нулю неопределенного разностного поля, соответственно,
равно нулю, то в силу нулевых начальных условий, соответственно, из первого или второго уравнения следует равенство нулю неопределенного разностного поля, соответственно,  или
или  , и единственность в этих частных случаях доказана.
, и единственность в этих частных случаях доказана.Предположим, что не равны нулю оба разностных поля. Если первое уравнение умножить на
 , а второе на
, а второе на  , и вычесть друг из друга, то получится следующее выражение:
, и вычесть друг из друга, то получится следующее выражение:
Это выражение можно проинтегрировать по объёму
 , и применить теорему Гаусса:
, и применить теорему Гаусса:![-2k\oint_s [\mathbf{e}\times\mathbf{h}]\,d\mathbf{s}
=
\frac{d}{d t}
\int_v (\mathbf{e}\cdot\hat{\varepsilon}\cdot\mathbf{e}+\mathbf{h}\cdot\hat{\mu}\cdot\mathbf{h})\, dv.](5a77e8e995639dd154a2ec8ea96f6e43.png)
Тангенциальные (касательные) к поверхности
 компоненты векторов
компоненты векторов  или
или  при любом
при любом  равны нулю (граничные условия), поэтому равен нулю и интеграл по поверхности. Следовательно:
равны нулю (граничные условия), поэтому равен нулю и интеграл по поверхности. Следовательно:
Полученное соотношение интегрируется по времени. Так как в начальный момент времени
 функции
функции  , то константа интегрирования равна нулю, и при любом
, то константа интегрирования равна нулю, и при любом  :
:
Подынтегральная функция является положительно определённой (всегда больше или равна нулю). Интеграл от такой функции равен нулю, только в том случае когда подынтегральная функция тождественно равна нулю. Следовательно, в любой момент времени внутри объёма
 и
и  . Поэтому решения совпадают.
. Поэтому решения совпадают.Для единственности решения уравнений Максвелла вместо задания тангенциальных компонент поля можно потребовать выполнение на границе условия импедансного типа
![\left(\mathbf{E}_\tau - Z [\mathbf{n}\times \mathbf{H}]\right)\Big|_s=0,](8420797e6d47806cd0f1abdf3a7820dc.png)
где импеданс
 выбран так, чтобы исключить приток энергии извне. Такое условие позволяет сформулировать теорему единственности и в неограниченном случае, при этом импедансное условие обращается в условие излучения Зоммерфельда на бесконечности.
выбран так, чтобы исключить приток энергии извне. Такое условие позволяет сформулировать теорему единственности и в неограниченном случае, при этом импедансное условие обращается в условие излучения Зоммерфельда на бесконечности.Для гармонических во времени процессов единственность решения задачи без начальных условий обеспечивается сколь угодно малым поглощением энергии внутри объёма
 или её утечкой через поверхность
или её утечкой через поверхность  (исключающими собственные колебания на действительных резонансных частотах).
(исключающими собственные колебания на действительных резонансных частотах).В стационарных задачах электростатики и магнитостатики единственное решение для установившихся полей определяется только граничными условиями.
Численное решение уравнений Максвелла
С развитием вычислительной техники, стало возможным решать многие задачи электродинамики численными методами[76], которые позволяют определить распределение электромагнитного поля при заданных начальных и граничных условиях, используя алгоритмы, основанные на уравнениях Максвелла.
Основными методами являются проекционные, в которых решение проецируется на какой-либо удобный функциональный базис, и дискретизационные — область пространства разбивается на множество малых конечных областей.
- В проекционном методе Бубнова — Галёркина[77] решение граничной задачи рассматривается в виде приближенного конечного разложения по базисным функциям. После подстановки разложения в исходные уравнения с учётом требования ортогональности получающейся невязки выбранным базисным функциям, получается система линейных уравнений для коэффициентов разложения.
Для компьютерных расчетов чаще применяются более универсальные дискретизационные методы:
- Метод конечных элементов (FEM), который используется для решения широкого класса задач, сводящихся к уравнениям в частных производных. В теории электромагнетизма чаще используется для расчёта задач электростатики, магнитостатики, распространения волн и квазистационарных явлений[78][79]. В методе конечных элементов рассматриваемая область пространства, в которой ищется решение, разбивается на большое число простых дискретных элементов, обычно, но не обязательно, треугольной (в двумерном случае) или тетраэдральной формы (в трёхмерном случае). Форма и плотность элементов адаптируются к требованиям задачи. Поведение отдельных элементов рассматривается как результат линейного взаимодействия соседних узлов решётки разбиения под действием внешних сил и описывается матричными уравнениями. Решение задачи сводится, таким образом, к решению разреженных систем большого числа линейных матричных уравнений. Метод реализован во многих коммерческих и свободных программных пакетах (см. статью Метод конечных элементов).
- Метод конечных разностей во временной области (FDTD) для нахождения временны́х и спектральных зависимостей[80][81] был разработан специально для решения уравнений Максвелла, в которых изменение электрического и магнитного поля во времени зависит от изменения, соответственно, магнитного и электрического поля в пространстве. В рамках этого метода область пространства и временной интервал подвергаются равномерной дискретизации с заданием начальных условий. Полученные из уравнений Максвелла конечно-разностные уравнения решаются в каждый последующий момент временной сетки, пока не будет получено решение поставленной задачи на всем требуемом временном интервале.
Источники
- ↑ Эрстед Г. Х. «Опыты, относящиеся к действию электрического конфликта на магнитную стрелку», в кн. Ампер А. М. Электродинамика. — М.: АН СССР, 1954. — С. 433-439. — 492 с. — 5000 экз.
- ↑ J.-B. Biot and F. Savart, Note sur le Magnétisme de la pile de Volta. — Annales Chim. Phys. — vol. 15. — pp. 222—223 (1820)
- ↑ Марио Льоцци История физики. — М.: Мир, 1970. — С. 253-257. — 464 с.
- ↑ Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля. — М.: ГИТТЛ, 1952. — С. 349. — 687 с. — 4000 экз.
- ↑ Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля. — М.: ГИТТЛ, 1952. — С. 632. — 687 с. — 4000 экз.
- ↑ Максвелл Дж. К. О фарадеевых силовых линиях в кн. Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля. — М.: ГИТТЛ, 1952. — С. 11—88. — 687 с. — 4000 экз.
- ↑ Maxwell J. C. On Faraday's Lines of Force // Transactions of the Cambridge Philosophical Society. — 1856. — Т. 10. — № 1. — С. 155—229.
- ↑ 1 2 3 Шапиро И. С. К истории открытия уравнений Максвелла // УФН. — 1972. — Т. 108. — № 2. — С. 319-333.
- ↑ Максвелл Дж. К. О физических силовых линиях в кн. Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля. — М.: ГИТТЛ, 1952. — С. 107—177. — 687 с. — 4000 экз.
- ↑ Maxwell J. C. On Physical Lines of Force // Philosophical Magazine : Ser. 4. — 1861,1862. — Т. 11,13. — С. 161—175, 281—291, 338—347; 12—23, 85—95.
- ↑ Максвелл Дж. К. Динамическая теория электромагнитного поля в кн. Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля. — М.: ГИТТЛ, 1952. — С. 251—316. — 687 с. — 4000 экз.
- ↑ Maxwell J. C. (1865). «A dynamical theory of the electromagnetic field». Philosophical Transactions of the Royal Society of London 155: 459—512.
- ↑ Maxwell J. C. A Treatise on Electricity And Magnetism, 1873
- ↑ Paul J. Nahin Oliver Heaviside: the life, work, and times of an electrical genius of the Victorian age. — JHU Press, 2002. — P. 108–112. — ISBN 9780801869099
- ↑ Aharonov, Y; Bohm, D (1959). «Significance of electromagnetic potentials in quantum theory». Physical Review 115: 485–491. DOI:10.1103/PhysRev.115.485.
- ↑ Nahin P. J. Oliver Heaviside: the life, work, and times of an electrical genius of the Victorian age. — JHU Press. — pp. 108—112. — ISBN 978-0-8018-6909-9
- ↑ 1 2 Einstein A. Zur Elektrodynamik bewegter Körper Ann Phys. — 1905. — Bd 17. — S. 891. Перевод: Эйнштейн А. К электродинамике движущихся тел в Эйнштейн А. Собрание научных трудов. — М.: Наука, 1965. — Т. 1. — С. 7-35. — 700 с. — 32 000 экз.
- ↑ Myron Evans Modern nonlinear optics. — John Wiley and Sons, 2001. — P. 240. — ISBN 9780471389316
- ↑ Larmor J. Aether and matter. — Cambridge. — 1900. — p. 162—193. Перевод: Лармор Дж. Эфир и материя в кн. Принцип относительности. Сборник работ по специальной теории относительности / Составитель Тяпкин А. А.. — М.: Атомиздат, 1973. — С. 47-64. — 332 с. — 3625 экз.
- ↑ Lorentz H. A. Electromagnetic Phenomena in a System Moving with any Velocity Smaller than that of Light. — Amst. Proc. — V. 6. — P. 809; 1904. — V. 12. — P. 986. Перевод: Лоренц Г. А. Электромагнитные явления в системе, движущейся с любой скоростью, меньшей скорости света в кн. Принцип относительности. Сборник работ по специальной теории относительности / Составитель Тяпкин А. А.. — М.: Атомиздат, 1973. — С. 67-86. — 332 с. — 3625 экз.
- ↑ Poincare H. Sur la dynainique de l’electron. — Comptes Rendues, Acad. Sci. — Paris. — 1905. — V. 140. — P. 1504. Перевод: Пуанкаре А. О динамике электрона в кн. Принцип относительности. Сборник работ по специальной теории относительности / Составитель Тяпкин А. А.. — М.: Атомиздат, 1973. — С. 90-93. — 332 с. — 3625 экз.
- ↑ Паули В. Теория Относительности. — М.: Наука. — С. 13-17.
- ↑ Исключением явились эксперименты Миллера на горе Маунт Вильсон. В дальнейшем повторение этих экспериментов другими исследователями на более точной аппаратуре эффекта не выявили. См. Повторения опыта Майкельсона
- ↑ Берестецкий, В. Б., Лифшиц, Е. М., Питаевский, Л. П. Квантовая электродинамика. — Издание 4-е, исправленное. — М.: Физматлит, 2002. — 720 с. — («Теоретическая физика», том IV). — ISBN 5-9221-0058-0
- ↑ Л. Б. Окунь Приложение I // Физика элементарных частиц. — М.: Наука, 1984.
- ↑ Д. В. Сивухин О международной системе физических величин (рус.) // УФН. — 1979. — Т. 129. — № 10. — С. 335.
- ↑ С. Г. Каршенбойм Фундаментальные физические константы: роль в физике и метрологии и рекомендованные значения (рус.) // УФН. — 2005. — Т. 175. — № 3. — С. 271.
- ↑ То есть содержащих дивергенции векторных полей, являющиеся скалярами.
- ↑ Например, в проводнике обычно присутствуют носители заряда как минимум двух типов разного знака, поэтому суммарная плотность заряда в проводнике может быть равна нулю, а ток тем не менее может присутствовать (и его плотность тогда нулю не равна).
- ↑ Болотовский Б. М. Оливер Хевисайд. — М.: Наука, 1985. — С. 43-44. — 260 с.
- ↑ O. Haviside, «On the Electromagnetic Effects due to the Motion of Electrification through a Dielectric», Phil.Mag. S.5 27, p. 324, 1889.
- ↑ Карцев В. П. «Приключения великих уравнений», М.: Знание, 1986.
- ↑ Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2008). CODATA Recommended Values of the Fundamental Physical Constants: 2006. Rev. Mod. Phys. 80: 633—730. doi:10.1103/RevModPhys.80.633.
- ↑ Значения физических постоянных
- ↑ Например, Таблицы физических величин / акад. И. К. Кикоин. — М.: Атомиздат, 1976.
- ↑ Refractive index database
- ↑ Стрэттон Дж. А. Теория электромагнетизма. — М.-Л.: ГИТТЛ, 1948. — С. 42-45. — 539 с. — 8000 экз.
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 112-113. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 69-76,95-96. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
- ↑ Стрэттон Дж. А. Теория электромагнетизма. — М.-Л.: ГИТТЛ, 1948. — С. 34-35. — 539 с. — 8000 экз.
- ↑ 1 2 Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 215-218. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
- ↑ Гинзбург В. Л. Теоретическая физика и астрофизика. — М.: Наука, 1981. — С. 12. — 503 с.
- ↑ Стрэттон Дж. А. Теория электромагнетизма. — М.-Л.: ГИТТЛ, 1948. — С. 37-40. — 539 с. — 8000 экз.
- ↑ Essex E. A. Hertz vector potentials of electromagnetic theory. — American Journal of Physics. — 45. — 1977. — 1099—1101.
- ↑ A. Nisbet, «Hertzian electromagnetic potentials and associated gauge transformations», Proc. of the Royal Soc. of London. Ser. A., 231, #1185, 250—263, 1955.
- ↑ P. Debye Der Lichtdruck auf Kugeln von beliebigem Material (нем.) // Annalen der Physik. — 1909. — Т. 30. — С. 57—136.
- ↑ Стрэттон Дж. А. Теория электромагнетизма. — М.-Л.: ГИТТЛ, 1948. — С. 345-348. — 539 с. — 8000 экз.
- ↑ R. Janaswamy A note on the {TE/TM} decomposition of electromagnetic fields in three dimensional homogeneous space (англ.) // IEEE Transactions on Antennas and Propagation. — 2004. — Т. 52. — С. 2474—2476.
- ↑ L. Silberstein Electromagnetische Grundgleichungen in bivectorieller Behandlung (нем.) // Annalen der Physik. — 1907. — Т. 22. — С. 579.
- ↑ 1 2 I. Bialynicky-Birula Photon wave function (англ.) // Progress in Optics. — 1996. — Т. 36. — С. 245—294.
- ↑ Стрэттон Дж. А. Теория электромагнетизма. — М.-Л.: ГИТТЛ, 1948. — С. 40—42. — 539 с. — 8000 экз.
- ↑ Здесь и ниже используются наиболее употребительные в современной литературе соглашения (о нумерации координат, сигнатуре метрики итп), которые вообще говоря могут быть выбраны и несколько по-другому, что встречается в литературе.
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 88-90. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
- ↑ Müller-Kirsten H. J. W. Electrodynamics: An Introduction Including Quantum Effects. — Singapore: World Scientific, 2004. — P. 398,399. — 522 p. — ISBN 981-238-807-9
- ↑ Müller-Kirsten H. J. W. Electrodynamics: An Introduction Including Quantum Effects. — Singapore: World Scientific, 2004. — P. 399. — 522 p. — ISBN 981-238-807-9
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 90-91. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
- ↑ Müller-Kirsten H. J. W. Electrodynamics: An Introduction Including Quantum Effects. — Singapore: World Scientific, 2004. — P. 403. — 522 p. — ISBN 981-238-807-9
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 70-73. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
- ↑ 1 2 Müller-Kirsten H. J. W. Electrodynamics: An Introduction Including Quantum Effects. — Singapore: World Scientific, 2004. — P. 428. — 522 p. — ISBN 981-238-807-9
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 102. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
- ↑ Болибрух А. А. Уравнения Максвелла и дифференциальные формы, МЦНМО, 2002.
- ↑ Мизнер Ч., Торн К., Уилер Дж. Гравитация. — М.: Мир, 1977. — Т. 1. — С. 195,196. — 474 с.
- ↑ Мизнер Ч., Торн К., Уилер Дж. Гравитация. — М.: Мир, 1977. — Т. 1. — С. 153-155. — 474 с.
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — С. 128-130. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
- ↑ Берклеевский курс физики. Том 2. Парселл Э. Электричество и магнетизм. — М.: Наука, 1971.
- ↑ Schwinger J. On gauge invariance and vacuum polarization (англ.) // Phys. Rev. Lett.. — 1951. — Т. 82. — С. 664.
- ↑ Heisenberg W., Euler H. Folgerungen aus der Dlracschen Theorie des Positrons (нем.) // Z. Phys.. — 1936. — Т. 98. — С. 714.
- ↑ А. В. Белинский, А. С. Чиркин Сжатое состояние — статья из Физической энциклопедии
- ↑ Парселл Э. Берклеевский курс физики. — М.: Наука. — Т. II. Электричество и магнетизм. — С. 149-181.
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
- ↑ von W. v. Ignatowsky «Einige allgemeine Bemerkungen zum Relativitätsprinzip» Verh. d. Deutsch. Phys. Ges. 12, 788-96, 1910 (русский перевод)
- ↑ von Philipp Frank und Hermann Rothe «Über die Transformation der Raumzeitkoordinaten von ruhenden auf bewegte Systeme» Ann. der Physik, Ser. 4, Vol. 34, No. 5, 1911, pp. 825—855 (русский перевод)
- ↑ Стрэттон Дж. А. Теория электромагнетизма. — М.-Л.: ГИТТЛ, 1948. — С. 429-430. — 539 с. — 8000 экз.
- ↑ Никольский В. В., Никольская Т. И. Электродинамика и распространение радиоволн. М.: Наука, 1989. — C. 128—130
- ↑ X. L. Zhou «On independence, completeness of Maxwell’s equations and uniqueness theorems in electromagnetics» Progress In Electromagnetics Research, PIER 64, 117—134, 2006 pdf
- ↑ Chew W. C., Jin J., Michielssen E., Song J. Fast and Efficient Algorithms in Computational Electromagnetics. — Artech House, 2001. — ISBN 1-58053-152-0
- ↑ Никольский В. В., Никольская Т. И. Электродинамика и распространение радиоволн. М.: Наука, 1989. — C. 416—436
- ↑ Сильвестер П. и Феррари Р. Метод конечных элементов для радиоинженеров и инженеров-электриков. — М.: Мир, 1986. — 336 с.
- ↑ Monk, P. Finite Element Methods for Maxwell's Equations. — Clarendon Press, Oxford, 2003.
- ↑ Taflove A. and Hagness S. C. Computational Electrodynamics: The Finite-Difference Time-Domain Method. — Artech House, 2005.
- ↑ Jin, J. The Finite Element Method in Electromagnetics. — 2nd. — Wiley-IEEE Press, 2002. — ISBN 0-47143-818-9
Примечания
См. также
- Электродинамика
- Квантовая электродинамика
- Максвелл, Джеймс Клерк
- Теория Янга — Миллса
- Потенциалы Лиенара — Вихерта
- Уравнения Ефименко
- Закон электромагнитной индукции Фарадея
Литература
Исторические публикации
- Ампер А. М. Электродинамика. — М.: АН СССР, 1954. — 492 с. — 5000 экз.
- Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля. — М.: ГИТТЛ, 1952. — 687 с. — 4000 экз.
- Максвелл Дж. К. Статьи и речи. — М.: Наука, 1968. — 423 с.
- Фарадей М. Экспериментальные исследования по электричеству. — М.: АН СССР, 1947—1959. — Т. I—III.
- Maxwell J. C. A dynamical theory of the electromagnetic field // Philosophical Transactions of the Royal Society of London. — 1865. — Т. 155. — С. 459—512.
- Maxwell J. C., A Treatise on Electricity And Magnetism — Volume 1 — 1873 — Posner Memorial Collection — Carnegie Mellon University
- Maxwell J. C., A Treatise on Electricity And Magnetism — Volume 2 — 1873 — Posner Memorial Collection — Carnegie Mellon University
- Maxwell J. C. On Physical Lines of Force // Philosophical Magazine : Ser. 4. — 1861,1862. — Т. 11,13. — С. 161—175, 281—291, 338—347; 12—23, 85—95.
- Maxwell J. C. On Faraday's Lines of Force // Transactions of the Cambridge Philosophical Society. — 1856. — Т. 10. — № 1. — С. 155—229.
История развития
- Болотовский Б. М. Оливер Хевисайд. — М.: Наука, 1985. — 260 с.
- Карцев В. П. Максвелл (Жизнь замечательных людей). — М.: Молодая гвардия, 1976. — 336 с.
- Карцев В. П. Приключения великих уравнений. — М.: Знание, 1986. — 288 с.
- Шапиро И. С. К истории открытия уравнений Максвелла // УФН. — 1972. — Т. 108. — № 2. — С. 319-333.
- Купер Л. Физика для всех. т.1 = Leon N. Cooper An Introduction to the Meaning and Structure of Phisics, 1968,1970. — М.: Мир, 1973.
Общие курсы физики
- Астахов А. В., Широков Ю. М. Курс физики, Т. II, Электромагнитное поле. — М.: Наука, 1980. — 360 с.
- Баскаков С. И. Основы электродинамики. — М.: Сов. радио, 1973. — 248 с.
- Калашников С. Г. Электричество (Общий курс физики, т. 2).. — М.: Физматлит, 6-е изд., 2003. — 624 с. — ISBN 5-9221-0312-1
- Матвеев А. Н. Электричество и магнетизм. — М.: Высшая школа, 1983.
- Никольский В. В., Никольская Т. И. Электродинамика и распространение радиоволн. М.: Наука, 1989.
- Пеннер Д. И., Угаров В. А. Электродинамика и специальная теория относительности. М.: Просвещение, 1980.
- Парселл Э. Электричество и магнетизм. Берклеевский курс физики. Том 2. М.: Наука, 1971.
- Сивухин Д. В. Общий курс физики. — Изд. 3-е, испр. и доп.. — М.: Наука, 1996. — Т. III. Электричество. — 320 с. — ISBN 5-02-014054-6.
- Тоннела М. А. Основы электромагнетизма и теории относительности. М.: ИЛ, 1962.
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Том 5. Электричество и магнетизм. М.: Мир, 1965
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Том 6. Электродинамика. М.: Мир, 1966
Курсы теоретической физики
- Баранов А. М., Овчинников С. Г., Золотов О. А., Паклин Н. Н., Титов Л. С. Теоретическая физика: Электродинамика. Электродинамика сплошных сред. Учебное пособие по курсу «Электродинамика и основы электродинамики сплошных сред» // СФУ, Красноярск, 2008. — 198 с.
- Джексон Дж. Классическая электродинамика. — М.: Мир, 1965.
- Ландау Л. Д., Лифшиц Е. М. Теория поля (Теоретическая физика, т. II). — М.: Физматлит, 2003. — 536 с. — ISBN 5-9221-0056-4
- Ландау Л. Д., Лифшиц Е. М. Электродинамика сплошных сред (Теоретическая физика, т. VIII). — М.: Физматлит, 2005. — 656 с. — ISBN 5-9221-0123-4
- Батыгин В. В., Топтыгин И. Н. Современная электродинамика. Часть 1. Микроскопическая теория. — М.: НИЦ «Регулярная и хаотическая динамика», 2005. — 736 с. — ISBN 5-93972-492-2
- Топтыгин И. Н. Современная электродинамика. Часть 2. Теория электромагнитных явлений в веществе. — М.: НИЦ «Регулярная и хаотическая динамика», 2005. — 848 с. — ISBN 5-93972-493-0
- Стрэттон Дж. А. Теория электромагнетизма. — М.-Л.: ГИТТЛ, 1948. — 539 с. — 8000 экз.
- Тамм И. Е. Основы теории электричества. — М.: Наука, 1989.
- Фущич В. И., Никитин А. Г. Симметрия уравнений Максвелла. — Киев: Наук. думка, 1983. — C. 200.
- Болибрух А. А. Уравнения Максвелла и дифференциальные формы. — МЦНМО, 2002.
Решения уравнений Максвелла
- Баландин М. Ю., Шурина Э. П. Векторный метод конечных элементов: Учебное пособие. — Новосибирск: НГТУ, 2001. — 69 с.
- Вайнштейн Л. А. Электромагнитные волны. — М.: Радио и связь, 1988.
- Вонсовский С. В. Магнетизм. Магнитные свойства диа-, пара-, ферро-, антиферро-, и ферримагнетиков. — М.: Наука, 1971.
- Гинзбург В. Л. Распространение электромагнитных волн в плазме. — 2-е изд. — М.: Наука, 1967.
- Сильвестер П. и Феррари Р. Метод конечных элементов для радиоинженеров и инженеров-электриков. — М.: Мир, 1986. — 336 с.
Ссылки
Эта статья входит в число избранных статей русскоязычного раздела Википедии. Это статья 2010 года русскоязычного раздела Википедии. Категории:- Электродинамика
- Дифференциальные уравнения в частных производных
- Физические законы и уравнения
Wikimedia Foundation. 2010.



















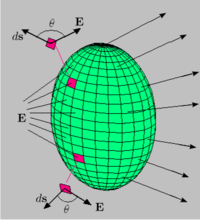
![\mathbf{F}=q\,\mathbf{E}+\frac{q}{c}\,[\mathbf{u}\times\mathbf{B}]](6d60f4deacd60aa62cf925bdd24db631.png)
![\mathbf{F}=q\,\mathbf{E}+q\,[\mathbf{u}\times\mathbf{B}]](5b78d80863962e4fde65e4e2e8585731.png)












![\nabla\cdot\mathbf{E}=4\pi[\rho_f+\rho_b]](91ce551d38b1b768563e6a15111ff5bb.png)
![\nabla\cdot\mathbf{E}= \frac{1}{\varepsilon_0}[\rho_f+\rho_b]](bae10ee03efc355b1e5d1c236260cba1.png)
![\nabla\times\mathbf{B}=\frac{4\pi}{c} [\mathbf{j}_b+\mathbf{j}_f]+\frac{1}{c}\frac{\partial\mathbf{E}}{\partial t}](ad634766c7ed24c865861c7fe7f22aba.png)
![\nabla\times\mathbf{B}= \mu_0[\mathbf{j}_b+\mathbf{j}_f]+\frac{1}{c^2}\frac{\partial\mathbf{E}}{\partial t}](d6d35a2b7829c950f45f1c4483e7fa58.png)










































![\Delta \mathbf {\Pi}^e - \frac{\mu}{c^2}\frac{\partial^2{\mathbf {\Pi}^e}}{\partial t^2} =- \frac{4\pi}{\varepsilon} \left[\mathbf {P}+\mathbf{P}_f\right].](ba809f59a92cf90bd88b359ebef5e96b.png)

![\Delta \mathbf {\Pi}^e - \frac{\mu}{c^2}\frac{\partial^2{\mathbf {\Pi}^e}}{\partial t^2} =- \frac{1}{\varepsilon\varepsilon_0} \left[\mathbf {P}+\mathbf {P}_f\right].](2d02d6b2ceb2b2ab9d0191b3fffedd9f.png)




![\mathbf {H}^m = \nabla\times[\nabla\times \mathbf{\Pi}^m] .](d21484a58440a9cb80a341742928e347.png)









![\mathbf F=\frac{1}{\sqrt{8\pi}}\left[\sqrt{\epsilon}\mathbf E+i\sqrt{\mu}\mathbf H\right],](06f6754f729913ee4530281c93a0b33d.png)
![\mathbf F=\frac{1}{\sqrt{2}}\left[\sqrt{\varepsilon\varepsilon_0}\mathbf E+i\sqrt{\mu\mu_0}\mathbf H\right],](5bb104ddff2e1d69d7ff3c0267bae97f.png)





























![\mathbf{S}=\frac{c}{16\pi}\left[{\tilde{\mathbf{E}}^*}\times{\tilde{\mathbf{H}}}+{\tilde{\mathbf{E}}}\times{\tilde{\mathbf{H}}^*}\right],](7229fab46779d32d9a201464478d15b9.png)


![\mathbf{S}=\frac{1}{4}\left[{\mathbf{E}^*}\times{\tilde{\mathbf{H}}}+{\tilde{\mathbf{E}}}\times{\tilde{\mathbf{H}}^*}\right],](6744b1a4a558cc1bceadc8e6d8d0d047.png)









![\nabla\times\tilde{\mathbf{B}}=-i\tilde{\varepsilon}\tilde{\mu}\frac{\omega}{c}\left[1+i\frac{4\pi \tilde{\sigma}}{\omega\tilde{\varepsilon}}\right]\tilde{\mathbf{E}}.](db41e8db4e838a86621d41a8519b8fca.png)
![\nabla\times\tilde{\mathbf{B}}= -i\tilde{\varepsilon}\tilde{\mu}\frac{\omega}{c^2}\left[1+i\frac{\tilde{\sigma}}{\omega\varepsilon_0\tilde{\varepsilon}}\right]\tilde{\mathbf{E}}.](7e92e0c1e9819392c3df0dd83c3cd59d.png)








![\nabla\times[\nabla\times\mathbf E]=\nabla\times\left(-\frac{\partial\mathbf B}{\partial t}\right)=-\frac{\partial}{\partial t}[\nabla\times\mathbf B]=-\frac{\varepsilon\mu}{c^2}\frac{\partial^2\mathbf E}{\partial t^2}.](51aa1d42179000d1c7538d87818d50db.png)
![\nabla\times[\nabla\times\mathbf E]=\nabla\,(\nabla\cdot\mathbf E)-\Delta\mathbf E = -\Delta\mathbf E,](3cbf5f4ebd333d40e87aed3aaceadc70.png)
![\mathbf{E}=\frac{Q}{\varepsilon}\, \frac{\mathbf{r}}{r^3}\, \frac{1-u^2/c^2}{(1-[\mathbf{n}\times\mathbf{u}]^2/c^2)^{3/2}}](80cfc8c9f731bc9a891d77f15be642fe.png)
![\mathbf{B}=\frac{\varepsilon\mu}{c}\,[\mathbf{u}\times \mathbf{E}]](0723ec68364c35a77e330113e26d8db5.png)
![\mathbf{E}=\frac{Q}{4\pi\varepsilon\varepsilon_0}\, \frac{\mathbf{r}}{r^3}\, \frac{1-u^2/c^2}{(1-[\mathbf{n}\times\mathbf{u}]^2/c^2)^{3/2}}](568acc44011d172ffc21afa8c3e232e5.png)
![\mathbf{B}=\frac{\varepsilon\mu}{c^2}\,[\mathbf{u}\times \mathbf{E}]](326b863ccc70ab1e9a18de6e3af49f28.png)
![\mathbf{B}=\sqrt{\varepsilon\mu}\,[\mathbf{n}\times\mathbf{E}]](83e0af5ad5ea616ba5010c45e330632e.png)
![\mathbf{B}=\frac{\sqrt{\varepsilon\mu}}{c}\,[\mathbf{n}\times\mathbf{E}]](c16be81ea5237f2f753be13f0565dcc9.png)