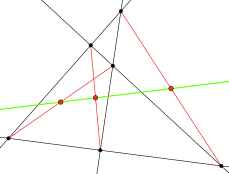
- Прямая Гаусса
-
Если никакие стороны четырёхугольника не параллельны, то середина отрезка, соединяющего точки пересечения противоположных сторон, лежит на прямой, соединяющей середины диагоналей. Эта прямая называется прямой Гаусса.
Эквивалентная формулировка:
Если прямая, не проходящая через вершины треугольника ABC, пересекает его стороны BC, CA, AB соответственно в точках
 , то середины отрезков
, то середины отрезков  коллинеарны.
коллинеарны.В этой формулировке можно заметить, что прямые
 равноправны. Они образуют конфигурацию, называемую четырёхсторонником. Прямая, на которой лежат середины указанных отрезков, называется прямой Гаусса четырёхсторонника.
равноправны. Они образуют конфигурацию, называемую четырёхсторонником. Прямая, на которой лежат середины указанных отрезков, называется прямой Гаусса четырёхсторонника.Утверждение о том, что середины трёх отрезков, концами, которых являются точки попарного пересечения четырёх прямых в общем положении, не лежащих на этих прямых, расположены на одной прямой, называется теоремой Ньютона.
Свойства
- Теорема выводится из теоремы Менелая.
- Прямая Гаусса перпендикулярна прямой Обера.
Источник
- Понарин Я. П. Элементарная геометрия. В 2 тт. — М.: МЦНМО, 2004. — С. 74. — ISBN 5-94057-170-0
 Категория:
Категория:- Планиметрия
Wikimedia Foundation. 2010.