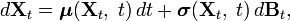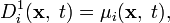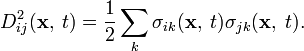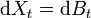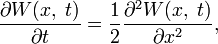Уравнение Фоккера — Планка

Уравнение Фоккера — Планка

Эволюция функции плотности вероятности согласно уравнению Фоккера — Планка.

Уравнение Фоккера — Планка — одно из стохастических дифференциальных уравнений, описывает временну́ю эволюцию функции плотности вероятности координат и импульса частиц в процессах, где важна стохастическая природа явления. Названо в честь нидерландского и немецкого физиков Адриана Фоккера и Макса Планка, также известно как прямое уравнение Колмогорова. Может быть обобщено на другие измеримые параметры (размер (в теории коалесценции), масса и т. д.).

Определение

Впервые уравнение было использовано для статистического описания броуновского движения частиц в воде. Хотя броуновское движение описывается уравнениями Ланжевена, которые могут быть решены численно методом Монте-Карло или методами молекулярной динамики, задачу в такой постановке часто трудно решить. И, вместо сложных численных схем, можно ввести функцию плотности вероятности 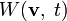$W(\mathbf{v},\;t)$, описывающую вероятность того, что частица имеет скорость в интервале 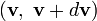$(\mathbf{v},\;\mathbf{v}+d\mathbf{v})$, если в момент времени 0 она имела начальную скорость 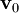$\mathbf{v}_0$, и записать для 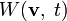$W(\mathbf{v},\;t)$ уравнения Фоккера — Планка.

Общая форма уравнения Фоккера — Планка для N переменных:

$\frac{\partial W}{\partial t}=\left[-\sum_{i=1}^N\frac{\partial}{\partial x_i}D_i^1(x_1,\;\ldots,\;x_N)+\sum_{i=1}^N\sum_{j=1}^N\frac{\partial^2}{\partial x_i\partial x_j}D_{ij}^2(x_1,\;\ldots,\;x_N)\right]W,$

где D¹ — вектор сноса и D² — тензор диффузии, причём диффузия вызвана действием сил стохастической природы.

Связь со стохастическими дифференциальными уравнениями

Уравнение Фоккера — Планка может быть использовано для расчёта плотности вероятности в стохастических дифференциальных уравнениях. Рассмотрим следующее стохастическое дифференциальное уравнение

$d\mathbf{X}_t=\boldsymbol{\mu}(\mathbf{X}_t,\;t)\,dt+\boldsymbol{\sigma}(\mathbf{X}_t,\;t)\,d\mathbf{B}_t,$

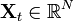где $\mathbf{X}_t\in\R^N$ — функция состояния системы, а 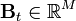$\mathbf{B}_t\in\R^M$ — стандартное N-мерное броуновское движение. Если начальное распределение задано как 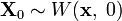$\mathbf{X}_0\sim W(\mathbf{x},\;0)$, то плотность вероятности 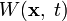$W(\mathbf{x},\;t)$ состояния системы 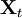$\mathbf{X}_t$ является решением уравнения Фоккера — Планка со следующими выражениями для сноса и диффузии соответственно:

$D^1_i(\mathbf{x},\;t)=\mu_i(\mathbf{x},\;t),$

$D^2_{ij}(\mathbf{x},\;t)=\frac{1}{2}\sum_k\sigma_{ik}(\mathbf{x},\;t)\sigma_{jk}(\mathbf{x},\;t).$

Пример

Стандартное скалярное уравнение броуновского движения генерируется следующим стохастическим дифференциальным уравнением:

$\ \mathrm{d}X_t=\mathrm{d}B_t$

Здесь скорость сноса равна нулю и коэффициент диффузии равен 1/2, следовательно, соответствующее уравнение Фоккера — Планка выглядит так:

$\frac{\partial W(x,\;t)}{\partial t}=\frac{1}{2}\frac{\partial^2 W(x,\;t)}{\partial x^2},$

это простейшая форма одномерного уравнения диффузии (теплопереноса).

Вывод

Первый согласованный вывод уравнения Фоккера — Планка на основе точной микроскопической динамики для классических и квантовых систем выполнен^[1] Н. Н. Боголюбовым и Н. М. Крыловым^[2] (переиздано в ^[3]).

См. также

• Цепочка уравнений Боголюбова
• Уравнение Лиувилля
• Уравнение Больцмана
• Уравнение Власова
• Уравнение Колмогорова — Чепмена
• Уравнения Навье — Стокса

Источники

• Hannes Risken, «The Fokker — Planck Equation: Methods of Solutions and Applications», 2nd edition, Springer, 1984. — 452 pages. — ISBN 3-540-61530-X.
• Лифшиц, Е. М., Питаевский, Л. П. Физическая кинетика. — М.: Наука, 1979. — 528 с. — («Теоретическая физика», том X). — 50 000 экз.

1. ↑ Боголюбов Н. Н. (мл.) и Санкович Д. П. (1993). «Николай Николаевич Боголюбов. Очерк научной деятельности.». Физика элементарных частиц и атомного ядра 24(5): 1224—1293.
2. ↑ Боголюбов Н. Н. и Крылов Н. М. (1939). Об уравнениях Фоккера — Планка, которые выводятся в теории возмущений методом, основанным на спектральных свойствах возмущённого гамильтониана. Записки кафедры математической физики Института нелинейной механики АН УССР 4: 5—80 (укр.).
3. ↑ Боголюбов Н. Н. Собрание научных трудов в 12 томах. Том 5: Неравновесная статистическая механика, 1939—1980. — М.: Наука, 2006. — ISBN 5020341428.