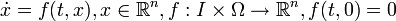Устойчивость динамических систем

Постановка задачи устойчивости динамических систем

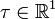Пусть Ω — область пространства $\mathbb{R}^n$, содержащая начало координат, $~I = [\tau; \infty]$, где $~\tau \in \mathbb{R}^1$. Рассмотрим систему (1) вида:

$\dot x = f(t, x), x \in \mathbb{R}^n, f: I \times \Omega \to \mathbb{R}^n, f(t, 0) = 0$

При любых 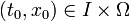$~(t_0, x_0) \in I \times \Omega$ существует единственное решение x(t, t₀, x₀) системы (1), удовлетворяющее начальным условиям x(t₀, t₀, x₀) = x₀. Будем предполагать, что решение x(t, t₀, x₀) определено на интервале 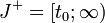$~J^+ = [t_0; \infty)$, причём $~J^+ \subset I$.

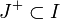Устойчивость по Ляпунову

Тривиальное решение x = 0 системы (1) называется устойчивым по Ляпунову, если для любых 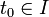$t_0 \in I$ и ε > 0 существует δ > 0, зависящее только от ε и t₀ и не зависящее от t, такое, что для всякого x₀, для которого 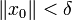$\|x_0\| < \delta$, решение x системы с начальными условиями x(t₀) = x₀ продолжается на всю полуось t > t₀ и удовлетворяет неравенству $\|x(t)\| < \epsilon$.

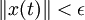Символически это записывается так:

$(\forall \epsilon > 0)(\forall t_0 \in I)(\exists \delta(t_0, \epsilon) > 0)(\forall x_0 \in B_{\delta(t_0, \epsilon)})(\forall t \ge t_0, t \in J^+) \Rightarrow (\|x(t, t_0, x_0)\| < \epsilon)$

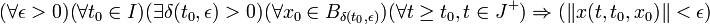
Равномерная устойчивость по Ляпунову

Тривиальное решение x = 0 системы (1) называется равномерно устойчивым по Ляпунову, если δ из предыдущего определения зависит только от ε:

$(\forall \varepsilon > 0)(\forall t_0 \in I)(\exists \delta(\varepsilon) > 0)(\forall x_0 \in B_{\delta(\varepsilon)})(\forall t \ge t_0, t \in J^+) \Rightarrow (\|x(t, t_0, x_0)\| < \varepsilon)$

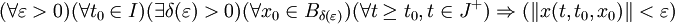
Неустойчивость по Ляпунову

Тривиальное решение x = 0 системы (1) называется неустойчивым по Ляпунову, если:

$(\exists \varepsilon > 0)(\exists t_0 \in I)(\forall \delta > 0)(\exists x_0 \in B_\delta)(\exists t_* \ge t_0, t_* \in J^+) \Rightarrow (\|x(t_*, t_0, x_0)\| \ge \varepsilon)$

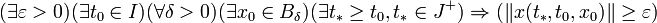
Асимптотическая устойчивость

Тривиальное решение x = 0 системы (1) называется асимптотически устойчивым, если оно устойчиво по Ляпунову и выполняется условие 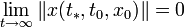$\lim_{t \to \infty} \|x(t_*, t_0, x_0)\| = 0$ для всякого x с начальным условием x₀, лежащим в достаточно малой окрестности нуля.

Эквиасимптотическая устойчивость

Тривиальное решение x = 0 системы (1) называется эквиасимптотически устойчивым, если оно равномерно устойчивое и равномерно притягивающее.

Равномерная асимптотическая устойчивость

Тривиальное решение x = 0 системы (1) называется равномерно асимптотически устойчивым, если оно устойчивое и эквипритягивающее.

Асимптотическая устойчивость в целом

Тривиальное решение x = 0 системы (1) называется асимптотически устойчивым в целом, если оно устойчивое и глобальнопритягивающее.

Равномерная асимптотическая устойчивость в целом

Тривиальное решение x = 0 системы (1) называется равномерно асимптотически устойчивым в целом, если оно равномерно устойчивое и равномерно- и глобальнопритягивающее.