- Разрешимое множество
-
В теории множеств, теории алгоритмов и математической логике, множество натуральных чисел называется разреши́мым или рекурси́вным, если существует алгоритм, который, получив на вход любое натуральное число, через конечное число шагов завершается и определяет, принадлежит ли оно данному множеству. Другими словами, множество является разрешимым, если его характеристическая функция вычислима. Множество, не являющееся разрешимым, называется неразреши́мым. Также можно говорить о разрешимом множестве, состоящем из любых конструктивных объектов, кодируемых натуральными числами. Любое разрешимое множество является перечислимым и арифметическим. Разрешимые множества соответствуют уровню
 арифметической иерархии (англ.).
арифметической иерархии (англ.).Существуют перечислимые множества, не являющиеся разрешимыми. Более того, перечислимое множество является разрешимым тогда и только тогда, когда его дополнение также перечислимо. Проекция разрешимого множества является перечислимой, но может не быть разрешимой. Подмножество разрешимого множества может не быть разрешимым (и даже может не быть арифметическим).
Совокупность всех разрешимых подмножеств
 является счётным множеством, а совокупность всех неразрешимых подмножеств
является счётным множеством, а совокупность всех неразрешимых подмножеств  — несчётным.
— несчётным.Примеры
- Пустое множество является разрешимым.
- Любое конечное множество и его дополнение являются разрешимыми множествами.
- Существуют бесконечные разрешимые множества с бесконечным дополнением. Например, множество всех чётных чисел и множество всех простых чисел являются разрешимыми.
- Дополнение разрешимого множества является разрешимым.
- Объединение и пересечение конечного числа разрешимых множеств также являются разрешимыми.
- Любое перечислимое множество, дополнение которого также перечислимо, является разрешимым (теорема Поста).
- Множество рациональных чисел, меньших числа π, является разрешимым.
- Множество, единственный элемент которого равен единице, если гипотеза Римана верна, и нулю в противном случае, является разрешимым (так как оно конечно).
- Множество номеров нетривиальных нулей ζ-функции, для которых нарушается гипотеза Римана, является разрешимым (хотя неизвестно, является ли оно пустым, конечным или бесконечным).
- Множество строк, являющихся правильными доказательствами в ZFC, разрешимо. Его проекция — множество утверждений, доказуемых в ZFC — перечислимо, но, при условии непротиворечивости ZFC — неразрешимо.
См. также
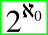 Категории:
Категории:- Теория множеств
- Математическая логика
- Теория алгоритмов
Wikimedia Foundation. 2010.
