- Метод трапеций
-
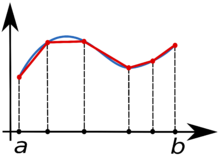
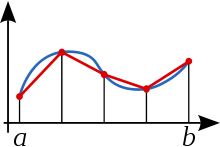
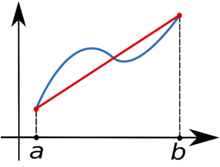 Аппроксимация функции линейной зависимостью при интегрировании методом трапеций
Аппроксимация функции линейной зависимостью при интегрировании методом трапеций
Метод трапеций — метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями. Алгебраический порядок точности равен 1.
Если отрезок
![\left[ a, b \right]\,\!](619595383f34b9fa837ae761c351bac7.png) является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по формуле
является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по формулеЭто простое применение формулы для площади трапеции — произведение полусуммы оснований, которыми в данном случае являются значения функции в крайних точках отрезка, на высоту (длину отрезка интегрирования). Погрешность аппроксимации можно оценить через максимум второй производной
Составная формула
Если отрезок
![\left[ a, b \right]\,\!](619595383f34b9fa837ae761c351bac7.png) разбивается узлами интегрирования и на каждом из элементарных отрезков применяется формула трапеций, то суммирование даст составную формулу трапеций
разбивается узлами интегрирования и на каждом из элементарных отрезков применяется формула трапеций, то суммирование даст составную формулу трапецийФормула Котеса
В случае равномерной сетки
где
 — шаг сетки.
— шаг сетки.Замечательные свойства
Метод трапеций быстро сходится к точному значению интеграла для периодических функций, поскольку погрешность за период аннулируется. Метод может быть получен путём вычисления среднего арифметического между результатами применения формул правых и левых прямоугольников.
В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.
Эта отметка установлена 9 октября 2011.Категория:- Численное интегрирование
Wikimedia Foundation. 2010.


![~\left| E(f) \right| \leqslant \frac{\left( b-a \right)^3}{12} \max_{x \in [a, b]} \left| f''(x) \right|\,.](1118228b885d5d2ba7027c06e222efe5.png)