- Дискретная теорема Грина
-
В дифференциальных исчислениях существует дискретная версия теоремы Грина, которая описывает отношение между двойным интегралом функции для обобщенной прямоугольной области D (область, которая образуется из конечного суммирования прямоугольников на плоскости) и линейной комбинации первообразной функции, заданной в углах области. В этом значении мы будем рассматривать популярную версию дискретной теоремы Грина.[1][2]
Теорема названа в честь британского математика Джорджа Грина, из-за сходства с его теоремой, теоремой Грина: обе теоремы описывают связь между интегрированием по кривой и интегрированием по области, ограниченной кривой.
Содержание
История
Теорема была впервые представлена как непрерывное продолжение алгоритма Ванга "Интегральное представление изображений", в 2007 году на Международной конференции по компьютерному видению ICCV [1], а затем вновь была опубликована профессором Doretto и его коллегами [3] в рецензируемом журнале в 2011 году.
Теорема
Предположим что ƒ является интегрируемой функцией на плоскости R2, так что:
является ее первообразной функцией. Пусть
 — обобщенная прямоугольная область. Тогда представим теорему как:
— обобщенная прямоугольная область. Тогда представим теорему как:где
 - множество углов данной области D ,
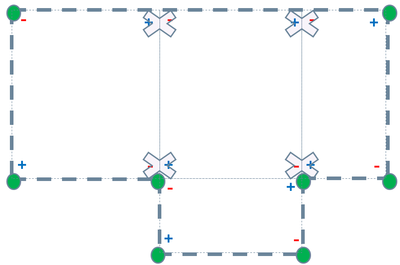
- множество углов данной области D ,  является дискретным параметром с возможными значениями {0, ±1, ±2}, которые определяются в зависимости от типа угла, как показано на рисунке справа. Этот параметр является частным случаем стремления кривой [4], которая последовательно определяется при помощи одностороннего разрыва [5] кривой в углах заданной области.
является дискретным параметром с возможными значениями {0, ±1, ±2}, которые определяются в зависимости от типа угла, как показано на рисунке справа. Этот параметр является частным случаем стремления кривой [4], которая последовательно определяется при помощи одностороннего разрыва [5] кривой в углах заданной области.Эта теорема является естественным продолжением алгоритма таблицы обобщённой области. Эта теорема расширяет алгоритм в том смысле, что область может быть непрерывной и она может быть сформирована из (конечного) числа прямоугольников, тогда как в алгоритме таблицы обобщённой области предполагается, что область является единым прямоугольником.
Дискретная теорема Грина также обобщает теорему Ньютона-Лейбница.
Концепция доказательства
Для доказательства теоремы можно применить формулу из алгоритма "Интегрального представление изображений" которая включает в себя прямоугольники образующие данную область:
Это изображение показывает, как + \ — коэффициенты первоначальной функции взаимно сокращаются в прямоугольниках, кроме точек расположенных в углах данной области.
Пример
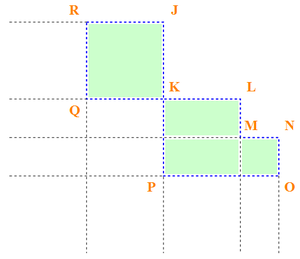
Предположим что функция ƒ, задана на плоскости R2 , тогда F является ее первообразной функцией. Пусть D — это область, окрашенная зеленым на следующем рисунке:
Согласно теореме, примененимой к данной области, получается следующее выражение:
Приложения
Дискретная теорема Грина используется в компьютерных приложениях по обнаружению объектов на изображениях и их быстрого вычисления, а также в интересах эффективного расчета вероятностей.
Обобщения
В 2011 году были предложены два обобщения к теореме:
- Подход, предложенний профессором Фам и его коллегами: обобщение теоремы полигональных областей с помощью динамического программирования [6].
- Подход, предложенный математиком Шахар: обобщение теоремы на более широкий спектр областей при помощью оператора разрыва [5] и метода интегрирования наклонной линии [7] при помощи которых и была сформулирована дискретная теорема Грина [8].
Видео лекции
См. также
Литература
- ↑ 1 2 Wang, Xiaogang; Doretto, Gianfranco; Sebastian, Thomas; Rittscher, Jens; Tu, Peter. "Shape and Appearance Context Modeling". in Proceedings of IEEE International Conference on Computer Vision (ICCV) 2007.
- ↑ Finkelstein, Amir (2010). "A Discrete Green's Theorem". Wolfram Demonstrations Project.
- ↑ Doretto, Gianfranco; Sebastian, Thomas; Rittscher, Jens; Tu, Peter. "Appearance-based person reidentification in camera networks: Problem overview and current approaches". Journal of Ambient Intelligence and Humanized Computing, pp. 1–25, Springer Berlin / Heidelberg, 2011.
- ↑ Finkelstein, Amir (2010). "Tendency of a Curve". Wolfram Demonstrations Project.
- ↑ 1 2 Finkelstein, Amir (2010). "Detachment and Tendency of a Single Variable Function". Wolfram Demonstrations Project.
- ↑ Pham, Minh-Tri; Yang Gao; Viet-Dung D. Hoang; Tat-Jen Cham. "Fast Polygonal Integration and Its Application in Extending Haar-like Features to Improve Object Detection". Proc. of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, 2010..
- ↑ Finkelstein, Amir (2010). "Extended Discrete Green's Theorem". Wolfram Demonstrations Project.
- ↑ Shachar, Amir. "On a Relation Between the Integral Image Algorithm and Calculus". arXiv:1005.1418v11[cs.DM], 2011.
Категория:- Дифференциальное исчисление
Wikimedia Foundation. 2010.