Черновики/Эмпирический критерий

Черновики/Эмпирический критерий

Эмпирический критерий (англ. empirical test) - это критерий, который традиционно применяется для проверки, будет ли последовательность случайной.

Далее рассмотрим двенадцать специфических критериев. Обсуждение каждого критерия разбивается на две части:

(a) "краткое" описание способов применения;

(b) теоретическое обоснование.

Каждый критерий применяется к последовательности

(U_n) = U₀, U₁, U₂,... (1)

действительных чисел, которые, как предполагается, независимы и равномерно распределены между 0 и 1. Некоторые из этих критериев предназначены непосредственно для целочисленных последовательностей, а не для последовательностей действительных чисел (1).

В таком случае вместо неё используется вспомогательная последовательность

(Y_n) = Y₀, Y₁, Y₂,..., (2)

определённая правилом

Y_n = [dU_n]. (3)

Эта последовательность целых чисел, которые, как предполагается, независимы и одинаково распределены между 0 и d-1. (Иначе говоря, вероятность, что случайная величина примет значение k, k = 0.....d-1, равна 1/d.) Число d выбирается таким, чтобы его было удобно использовать в том либо ином смысле. Например, можно выбрать d = 64 = 2⁶ на бинарном компьютере так, что Y_n представляет шесть старших двоичных разрядов двоичного представления числа U_n. Значение d должно быть достаточно большим, чтобы критерий стал практически неприменим.

Критерий равномерности (критерий частот)

Первое требование, предъявляемое к последовательности (1), состоит в том, что её члены - это числа, равномерно распределённые между 0 и 1. Существует два способа проверить это.

(a) Использовать критерий Колмогорова-Смирнова с F(x) = x для 0 <= x <= 1.

(b) Использовать последовательность (2) вместо (1), где d - подходящее число, например 100 на десятичном либо 64 или 128 - на бинарном компьютере. Для каждого r, 0 <= r < d, подсчитаем число случаев, когда Y_j = r для 0 <= j < d, а затем применим χ²-критерий, принимая k = d и вероятность p_s 1/d для каждой категории.

Критерий серий

Более общее требование к последовательности состоит в том, чтобы пары последовательных чисел были равномерно распределены независимым образом.

В критерий серий просто подсчитываем число случаев, когда пара (Y_2j, Y_2j+1) = (q, r) для 0 <= j < n. Такая операция осуществляется для каждой пары целых чисел (q, r), таких, что 0 <= q, r < d. Затем применяем χ²-критерий к этим k = d² категориям, где 1/d² - вероятность отнесения пары чисел к каждой из категорий. Как и для критерия равномерности, d - подходящее число, но оно должно быть немного меньшим, чем значения, предложенные выше, так как значимый χ²-критерий должен иметь n сравнительно большим по сравнению с k (скажем, по крайней мере n >= 5d²).

Ясно, что можно обобщить этот критерий для троек, четвёрок и т.д. вместо пар. Тогда значение d необходимо существенно уменьшить для того, чтобы число категорий не получилось слишком большим. Поэтому при рассмотрении четвёрок и больших серий чисел используются менее точные критерии, такие как покер-критерий и максимум критерий, описанные ниже.

Заметим, что 2n чисел последовательности (2) использовались в этом критерии для того, чтобы сделать n наблюдений. Было бы ошибкой применять критерий к серий к парам (Y₀,Y₁), (Y₁,Y₂), ..., (Y_n-1,Y_n). Но можно применить критерий серий ещё и к парам (Y_2j+1, Y_2j+2), ожидая, что наша последовательность удовлетворит этим двум проверкам. Однако нужно помнить, что эти проверки на самом деле взаимозависимы. С другой стороны, Джордж Марсалья доказал, что если использовать пары U_j, U_j+1, ..., U_n-1 и применять обычный χ²-критерий для вычисления обеих статистик (V₂ для критерия серий и V₁ - для критерия частот по Y₀, ..., Y_n-1) с тем же значением d, то случайная величина V₂ − V₁ будет иметь χ²-распределение с d(d − 1) степенями свободы, когда n достаточно большое.

Критерий интервалов

Этот критерий используется для проверки длины "интервалов" между появлением U_j на определённом отрезке. Если α и β - два действительных числа, таких, что 0 <= α < β <= 1, то рассмотрим длины подпоследовательностей U_j, U_j+1, ..., U_n-1, в которых U_j+r лежит между α и β, а другие U_s не лежат между этими числами. (Эту подпоследовательность, состоящую из r + 1 числа, будем называть интервалом длиной r.)

Покер-критерий (критерий разбиений)

Классический покер-критерий рассматривает n групп по пять последовательных целых чисел {Y_5j, Y_5j+1, Y_5j+2, Y_5j+3, Y_5j+4} для 0 <= j < nи проверяет, какие из следующих семи комбинаций соответствуют таким пятёркам чисел (порядок не имеет значения).

Все числа разные: abcde

Одна пара: aabcd

Две пары: aabbc

Три числа одного вида: aaabc

Полный набор: aaabb

Четыре числа одного вида: aaaab

Пять чисел одного вида: aaaaa

χ²-критерий основан на подсчёте числа пятёрок в каждой категории.

В общем случае можно рассматривать n групп k последовательных чисел и подсчитывать число групп из k чисел с r различными числами. Затем применяется χ²-критерий, в котором используются вероятности того, что в группе r различных чисел

p_r = (d(d - 1)...(d - r + 1)) / d^k {k r}. (5)

Так как вероятности p_r очень малы, когда r = 1 или 2, следует, вообще говоря, перед применением χ²-критерия объединить несколько категорий, имеющих малые вероятности, в одну.

Чтобы получить формулу для p_r, следует подсчитать, сколько d^k групп из k чисел, расположенных между 0 и d - 1 имеют точно r различных элементов, и разделить это число на d^k. Так как d(d - 1)...(d - r + 1) - это число упорядоченных наборов из r элементов множества, содержащего d элементов, достаточно показать, что {k r} - это число способов разбиения множества из k элементов на точно r частей.

Критерий собирания купонов

Следующий критерий относится к покер-критериям, так как критерий интервалов соотносится с критерием частот. Используется последовательность Y₀, Y₁,... и находятся длины отрезков Y_j+1, Y_j+2,..., Y_j+r, содержащие "полный набор" целых чисел от 0 до d - 1.

Критерий перестановок

Разделим последовательность на выходе на n групп по t элементов в каждой, т.е. (U_jt, U_jt+1,..., U_jt+t-1) для 0 <= j < n. Элементы в каждой группе можно упорядочивать t! различными способами. Подсчитывается число групп с любым возможным порядком и применяется χ²-критерий с k = t! возможными категориями и вероятностью 1/t! для каждой категории.

например, если t = 3, существует шесть возможных категорий, а именно U_3j+1 < U_3j+2 < U_3j+2, или U_3j < U_3j+2 < U_3j+1, или ..., или U_3j+2 < U_3j+1 < U_3j. В этом критерии предполагается, что U_s не могут быть равны между собой, т.е. вероятность того, что U_s = U_j при s ≠ j равно нулю.

Критерий монотонности

В последовательности можно проверять распределение восходящих и нисходящих серий. Имеется в виду проверка распределений длин монотонных частей заданной последовательности (отрезки возрастания или убывания).

В качестве примера точного определения серии рассмотрим последовательность цифр "1298536704". Проводя вертикальные линии слева, справа, а также между X_j и X_j+1 всякий раз, когда X_j > X_j+1, получим |1 2 9|8|5|3 6 7|0 4|.

Таким образом выделяются восходящие серии: сначала - серия длиной 3, затем - две серии длиной 1, затем снова серия длиной 3 и, наконец, серия длиной 2.

Мы не будем применять χ²-критерий к подсчёту серий, как в критерии интнрвалов и критерии собирания купонов (которые во многих отношениях подобны этому критерию), поскольку смежные интервалы не являются независимыми.

Критерий "максимум-t

Обозначим V_j = max (U_tj, U_tj+1,...,U_tj+t-1) для 0 <= j < n. Применим критерий Колмогорова-Смирнова к последовательности V₀, V₁,...,V_n-1. Таким образом проверим гипотезу о том, что функция распределения V_j равна F(x) = x^t, 0 <= x <= 1. Можно также применить критерий Колмогорова-Смирнова к последовательности V₀^t, V₁^t,..., V_n-1^t, проверяя гипотезу о равномерном распределении.

Для обоснования критерия необходимо показать, что функция распределения V_j равна F(x) = x^t. Вероятность того, что max(U₁, U₂, ..., U_t) <= x, равна вероятности того, что одновременно U₁ <= x, U₂ <= x, ..., U_t <= x, которая, в свою очередь, равна произведению вероятностей U_k <= x при k = 1,..., t, а именно - xx...x = x^t.

Критерий конфликтов

χ2-критерий можно применять только тогда, когда ненулевое число элементов ожидается в каждой категории. Но существует критерий другого вида, который можно использовать, когда число категорий намного больше числа наблюдений. Этот критерий имеет отношение к рандомизации - важному методу информационного поиска.

Предположим, что есть m урн, и поместим в них наудачу n, причём m намного больше n. Большинство шаров попадёт в пустые урны, но если шар попадёт в урну, в которой уже содержится хотя бы один шар, то будем говорить, что произошёл "конфликт". Критерий конфликтов подсчитывает число конфликтов, и генератор удовлетворяет этому критерию, если не возникает слишком много или слишком мало конфликтов.

Для определённости предположим, что m = 2²⁰ и n = 2¹⁴. Тогда в среднем на 64 урны приходится только один шар. Вероятность того, что в конкурентную урну попадёт ровно k шаров, равна p_k = (n k)m^-k(1 - m⁻¹)^n-k, поэтому среднее число конфликтов в урне равно

$\sum_{k>=1} \left(k - 1)p_k\right) = \sum_{k>=1} \left(kp_k)\right) - \sum_{k>=0} \left(p_k)\right) = n/m - 1 + p_0$.

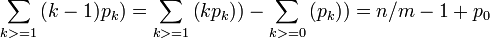Так как p₀ = (1 - m⁻¹)ⁿ - 1 - nm⁻¹ + (n 2)m⁻² - маленькое число, получим, что общее среднее число конфликтов во всех m урнах намного меньше n²/(2m) = 128. (Истинное значение равно ≈ 127,33.)

Критерий конфликтов можно использовать для того, чтобы оценивать генератор случайных чисел для строк больших размерностей. Например, когда m = 2²⁰ и n = 2¹⁴, можно проверять 20-мерную случайность генератора случайных чисел, положив d = 2 и сформировав 20-мерный вектор V_j = (Y_20j, Y_20j+1,...,Y_20j+19) для 0 <= j < n. Мы храним таблицу из m = 2²⁰ двоичных разрядов для определения конфликтов и один двоичный разряд для каждого возможного значения координаты вектора V_j; на компьютере с 32 двоичными разрядами в слове это даёт 2¹⁵ слов. Сначала во все 2²⁰ двоичных разрядов таблицы занесём 0; затем для каждого V_j, если в соответствующий двоичный разряд уже занесена 1, регистрируем конфликт, в противном случае заносим в двоичный разряд 1. Этот критерий можно использовать для размерности 10 при d = 4 и т.д.

Чтобы решить, проходит ли последовательность это испытание, можно использовать следующую таблицу процентных точек, когда m = 2²⁰ и n = 2¹⁴.

Конфликты <= 101 108 119 126 134 145 153

с вероятностью .009 .043 .244 .476 .742 .946 .989

Для определения этих вероятностей используется та же теория, что и для покер-критерия (5); вероятность, что произойдёт c конфликтов, равна вероятности того, что будут заняты n - c урн, а именно

(m(m-1)...(m - n + c + 1))/mⁿ {n n - c }.

Критерий промежутков между днями рождений

Джордж Марсалья в 1984 году ввёл новый критерий. Поместим n шаров в m урн, как и в критерии конфликтов, но под урнами подразумеваем дни года, а под шарами - дни рождения. Предположим, что (Y₁,...,Y_n) - это дни рождения, где 0 <= Y_k < m. Расположим их в порядке неубывания Y₍₁₎ < = ... <= Y_(n), определим n "промежутков" S₁ = Y₍₂₎ - Y₍₁₎, ..., S_n-1 = Y_(n) - Y_(n-1), S_n = Y₍₁₎ + m - Y_(n) и, наконец, расположим промежутки в таком порядке: S₍₁₎ <= ... <= S_(n). Пусть R - число равных промежутков, а именно - число индексов j, таких, что 1 < j <= n и S_(j) = S_(j-1). Когда m = 2²⁵ и n = 512, должно получится следующее.

R = 0 1 2 3 или больше

С вероятностью .368801577 .369035243 .183471182 .078691997

(Среднее число равных промежутков для выбранных m и n должно быть равным приблизительно 1.) Примените этот критерий, скажем, 1 000 раз и воспользуйтесь χ²-критерий с тремя степенями свободы, чтобы сравнить эмпирические значения R_i с правильным распределением. Так можно выяснить, будет ли генератор вырабатывать приемлемые случайные промежутки между днями рождения.

Такой критерий, как критерий промежутков между днями рождений, в первую очередь важен в связи с тем замечательным фактом, что генератор Фибоначчи с запаздыванием не удовлетворяет этому критерию, хотя он вполне удовлетворяет другим традиционным критериям. Рассмотрим, например, последовательность

X_n = (X_n-24 + X_n-56)mod m.

Числа этой последовательности удовлетворяют соотношению

X_n + X_n-86 = X_n-24 + X_n-31 (по модулю m),

так как обе стороны конгруэнтны X_n-24 + X_n-55 + X_n-86. Поэтому две пары разностей равны

X_n - X_n-24 = X_n-31 - X_n-86

и

X_n - X_n-31 = X_n-24 - X_n-86.

Всякий раз, когда X_n приемлемо близко к X_n-24 или X_n-31 (как должно было бы произойти в настоящей случайной последовательности), одна и та же разность имеет хороший шанс появиться в двух промежутках. Получится значительно больше случаев равенств (обычно со средним R ≈ 2, а не 1). но если исключить из R любой равный промежуток, возникающий из условий конгруэнтности, то полученная статистика R` будет удовлетворять критерию дней рождений.

Критерий сериальной корреляции

Критерий подпоследовательностей

Внешние программы часто вызывают случайные числа пакетами. Например, если программа работает со случайными переменными X, Y ,Z, она может потребовать одновременного генерирования трёх случайных чисел. В таких ситуациях важно, чтобы подпоследовательность, образующая каждую тройку членов первоначальной последовательности, была случайной. Если программа требует сразу q чисел, то последовательность

U₀, U_q, U_2q,...; U₁, U_q+1, U_2q+1,...; U_q-1, U_2q-1, U_3q-1,...

может быть проверена с помощью описанных выше критериев для первоначальной последовательности U₀, U₁, U₂,...

Опыты с линейными конгруэнтными последовательностями показали, что поведение этих порождённых последовательностей редко бывает менее случайным, чем поведение первоначальной последовательности, если только q не имеет большого множителя, общего с длиной периода. На бинарном компьютере с m, равным длине компьютерного слова, например, критерий подпоследовательностей для q = 8 даст результаты, худшие среди всех q < 16 , а на десятичном компьютере значение q = 10 приведёт к получению наиболее неудовлетворительных подпоследовательностей.

История

Статистические критерии, естественно, возникли в связи с потребностью доказать или опровергнуть гипотезы относительно различных наблюдений. Хорошо известны две ранние работы, посвящённые проверке случайности искусственно генерируемых чисел. Это две статьи М. Дж. Кендалла и Б. Бабингтон-Смита (M. G. Kendall and B. Babington-Smith, Jornal of Royal Statistical Society 101 (1938), 147-166; также в этом журнале см. 6 (1939), 51-61). В приведённых работах внимание было сосредоточено в большей степени на поверке случайности цифр между 0 и 9, чем на случайность реальных чисел; с этой целью авторы обсуждали критерий частот, критерий серий, критерий интервалов и покер-критерий, однако они неудачно применяли критерий серий. Кендалл и Бабингтон-Смит использовали также вариант критерия собирания купонов.

Критерий монотонности имеет довольно интересную историю. Первоначально он рассматривался для восходящих и нисходящих серий одновременно. Восходящие серии следовали за нисходящими, затем - восходящие серии и т.д. Заметим, что критерий монотонности и критерий перестановок зависят не только от ого, имеет ли U_n равномерное распределение, а от того факта, что U_i = U_j появляется с вероятность 0, когда i ? j. Поэтому данные критерии могут применяться ко многим типам случайных последовательностей. Критерий монотонности в примитивной форме введён И. Ж. Бьенэйме. Примерно через шестьдеят лет В. О. Кермак и А. Г. Мак-Кендрик опубликовали две обширные статьи на эту тему.^[1] В качестве примера они установили, что количество выпавших в Эдинбурге осадков между 1785 и 1930 годами носило "всецело случайных характер" по отношению к критерию монотонности (хотя они проверяли только среднее и стандартное отклонения длин серий). Другие исследователи также начали использовать этот критерий, но только в 1944 году было показано, что использовать χ²-метод в этом критерии неправомочно. В работе Х. Левена и Я. Вольфвица ^[2] введён правильный критерий монотонности (для чередующихся восходящих и нисходящих серий). В ней также обсуждались ошибки при использовании этого критерия ранее.

Среди всех рассмотренных выше критериев критерий частот и критерий сериальной корреляции кажутся более слабыми в том смысле, что почти все генераторы случайных чисел им удовлетворяют.

Критерий конфликтов также заслуживает самых наилучших рекомендаций, так как он предназначен специально для определения недостатков многих, к сожалению, широко распространённых генераторов. Основанный на идеях Х. Делгаса Христиасена^[3] (H. Delgas Chtistiandersen), этот критерий получил распространение с появлением компьютеров; он предназначен для использования на компьютере и не подходит для вычислений вручную.

Необходимость проверки последовательности с помощью нескольких критериев неоднократно отмечалась в литературе. Исследователи проверили, например, что некоторые генераторы чисел наподобие метода средин квадратов удовлетворяли критерию частот, критерию интервалов и покер-критерию, однако не удовлетворяли критерию серий. Линейные конгруэнтные последовательности с малым множителем, как известно, были проверены многими критериями, однако не выдержали проверку критерием монотонности, так как уних слишком мало серий единичной длины. Критерий "максимум-t" можно также использовать для поиска плохих генераторов, которые без проверки этим критерием кажутся вполне респектабельными. Генератор "вычитания с заимствованием" не проходит проверку критерием интервалов, когда максимальная длина интервала проевышает самое большое запаздывание. ^[4] Генератор Фибоначчи с запаздыванием, для которого теоретически гарантировано, что он имеет равнораспределённые младшие значащие разряды, тем не менее не удовлетворяет простым вариантам одноразрядного критерия равномерности.

Возможно, основной смысл экстенсивной проверки генераторов случайных чисел состоит в том, что людям, неправильно применяющим генератор случайных чисел господина Х, будет тяжело допустить, что на самом деле неправильна их собственная программа. Они будут обвинять генератор до тех пор, пока господин Х не докажет им, что его числа достаточно случайны. С другой стороны, если источник случайных чисел предназначен только для личного использования господином Х, последний может не беспокоится о его проверке, так как с большой вероятностью технических рекомендаций, приведённых в настоящей главе, достаточно для проверки этого датчика.

Чем больше испльзуются компьютеры, тем больше необходимо случайных чисел, которые раньше считались вполне удовлетворительными, теперь недостаточно хороши для применения в физике, комбинаторике, стохастической геометрии и т.д. Джордж Марсалья в связи с этим ввёл строгие критерии, которые превосходят классические методы, подобные критерию интервалов и покер-криетрию, в том смысле, что они по сравнению с этими критериями замечают другие отклонения. Например, он нашёл, что последовательность X_n+1 = (62605X_n + 113218009)mod 2²⁹ имеет значительное отклонение в следующем эксперименте. Было получено 2²¹ случайных чисел X_n и выделено 10 их старших двоичных разрадов Y_n = [X_n/2¹⁹]. Подсчитано, сколько из 2²⁰ возможных пар (y, y' ) 10-разрядных чисел не появятся среди (Y₁, Y₂), (Y₂, Y₃), ..., (Y_2²¹-1, Y_2²¹). Должно быть примерно 141909.33 отсутствующих пар со стандартным отклонением ≈ 290.46. Но в шести последовательных испытаниях, начиная с X₁ = 1.5 и 3.5, которое получилось слишком низким. Распределение оказалось слишком "плоским" для того, чтобы быть случайным, поскольку, вероятно, из 2²¹ чисел значимыми дробями являются только 1/256 на весь период. Подобный генератор с множителем 69069 и модулем 2³⁰, как показано, является лучшим. Марсалья и Земан (Zaman) назвали эту процедуру "обезьяний критерий", так как она позволяет подсчитать количество двухсимвольных комбинаций, которые обезьяна пропустит после печатанья на клавиатуре с 1024 клавишами.^[5]

См. также

• Распределение Колмогорова
• Распределение хи-квадрат

Литература

• D. E. Barton and C. L. Mallows, Annals Math. Stat. 36 (1965), 236-260.
• J. Bienayme`, Comptes Rendus Acad. Sci. Paris 81 (1875), 417-243.
• R. E. Greewood, Math. Comp. 9 (1955), 1-5.
• Дональд Э. Кнут Искусство программирования. Том 2 = The Art of Computer Programming, Volume II. Third Edition. — 3-е изд. — М.: "Вильямс", 2007.

Примечания

1. ↑ см. W. O. Kermack and A. G. McKendrick, Proc. Royal Society Edinburgh 57 (1937), 228-240, 332-376).
2. ↑ см. H. Levene and J. Wolfowitz, Annals Math. Stat. 15 (1944), 58-69.
3. ↑ Inst. Math. Stat. and Oper. Res., Tech. Univ. Denmark (Oktober, 1975); не опубликовано.
4. ↑ см. Vatullainen, Kankaala, Saarienen, and Ala-Nissila, Computer Physics Communicayions 86 (1995), 209-226.
5. ↑ Computers and Math. 26, 9 (November, 1993), 1-10, где приведён анализ нескольких "обезьяних критериев".