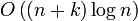Алгоритм Бентли — Оттмана

Алгоритм Бентли — Оттмана

Алгоритм Бентли — Оттмана (1979) позволяет найти все точки пересечений прямолинейных отрезков на плоскости. В нем применяется метод выметающей прямой ( = заметающей прямой, движущейся прямой, сканирующей линии; англ. sweeping line). В методе используется вертикальная выметающая прямая движущаяся слева направо, при этом отрезки, которые она пересекает при данной координате x, можно упорядочить по координате y, тем самым их можно сравнивать между собой (какой выше, какой ниже). Это сравнение можно осуществить, например, используя уравнение прямой, проходящей через две точки (отрезки заданы двумя своими конечными точками): 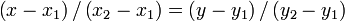$\left(x - x_1 \right)/ \left(x_2 - x_1 \right) = \left(y - y_1 \right)/ \left(y_2 - y_1 \right)$, где x₁, y₁ и x₂, y₂ — координаты, соответственно, первой и второй точек отрезка. Выметающая прямая перемещается по так называемым точкам событиям (левым и правым концам отрезков, а также точкам пересечения отрезков). После точки пересечения отрезки следует менять местами, так как, например, самый верхний из пересекающихся отрезков после точки пересечения становится самым нижним. Приведенный ниже алгоритм не рассчитан на случай, когда два отрезка пересекаются больше, чем в одной точке.

NB Выметающую прямую можно также представить как горизонтальную, движущуюся сверху вниз по координате y, и сравнивать пересекающие ее отрезки по координате x.

Пересечение отрезков $O \left( \left(n + k \right)\log n \right)$

Обработка вертикальных отрезков

Возникает проблема с вертикальным отрезком в том смысле как его сравнивать на выше/ниже с пересекающими отрезками. Для этого можно, например, считать, что если точка пересечения вертикального с не вертикальным отрезков находится ниже текущей координаты y точки события, то вертикальный отрезок находится выше, если точка пересечения выше текущей координаты y точки события, то вертикальный отрезок считается ниже пересекающего его. Если текущая координата y равна координате y точки события, то при удалении отрезка считать, что вертикальный отрезок ниже, при вставке же считать, что он выше.

Квадрат памяти

В худшем случае, когда, например, все отрезки, пересекаясь между собой, образуют прямоугольную сетку, будет 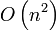$O \left(n^2 \right)$ точек пересечений, которые надо будет хранить. Чтобы избежать использования квадрата памяти в алгоритме, можно удалять точку пересечения отрезков, которые временно перестают быть соседними при данном положении выметающей прямой. Эти точки все равно будут снова найдены при последующих шагах алгоритма, когда данные отрезки снова станут соседними (Печ, Шерир 1991).

Алгоритм

В приведенном ниже псевдокоде используются:

• Q — динамические структура данных без повторений с логарифмическим временем поиска, вставки, удаления точек событий и поиска минимального элемента (например, красно-чёрное дерево, 2-3-дерево).
• T — динамические структура данных без повторений с логарифмическим временем поиска, вставки, удаления отрезков. В ней хранятся все отрезки, пересекающие выметающую прямую (например, красно-чёрное дерево, 2-3-дерево).
• q — точка события.
• newq — только что найденная точка пекресечения отрезков, точка события.
• L(q) — множество отрезков, левый конец которых — q (для вертикальных отрезков левым считается нижний конец).
• R(q) — множество отрезков, правым концом которых является q.
• I(q) — множество отрезков, пересекающихся в q.

segmentsIntersections(points[])
    1) Инициализируются Q и T. В Q заносятся все концы отрезков, упорядоченные по координате x, при этом, если две точки совпали,
       то левая конечная точка отрезка помещается перед правой. Если совпали только x, то точка с меньшим y является меньшей.
       T ← ∅
    2) while Q != ∅
           q ← min(Q);
           processPoint(q);

processPoint(q)
    1) Найти в Q все отрезки, содержащие q; // они в Q будут соседними, так как точки события, которые содержатся в этих
       отрезках, имеют одинаковые координаты;
    2) if (|L(q)| + |R(q)| + |I(q)| > 1) ИЛИ (|I(q)| > 0)
           then Выдать в ответ точку q;
    3) if (|I(q)| = 0) И (|L(q)|+|R(q)| > 0) // в рассматриваемой точке все отрезки только начинаются или заканчиваются;
           then I(q) ← I(q) ∪ L(q) ∪ R(q); // добавить в I(q) L(q) и R(q)
    4) Удалить из T R(q) и I(q);
    5) Вставить в T I(q) и L(q);
    // из T были удалены все отрезки из множества I(q), теперь же вставляются обратно в измененном порядке после точки пересечения;
    6) if (L(q)∪I(q) = ∅) ИЛИ (|I(q)| = |R(q)| - 1)
           then Найти в T верхнего и нижнего соседей q su и sl;
                newq = findIntersect(su, sl);
                if newq != NULL
                    then add(Q, newq);
    7) else
           Пусть s′ — самый верхний отрезок из L(q)∪I(q);
           Пусть su — верхний сосед s′ в T;
           Пусть s′′ — самый нижний отрезок из L(q)∪ I(q);
           Пусть sl — нижний сосед s′′ в T;
           newq = findIntersect(su, s′);
           if newq != NULL
               then add(Q, newq);
           newq = findIntersect(sl, s′′);
           if newq != NULL
               then add(Q, newq);
           // далее убираем квадрат памяти;
           newq = findIntersect(sl, su);
           if newq != NULL
               then delete(Q, newq);
           newq = findIntersect(s′′, su);
           if newq != NULL
               then delete(Q, newq);
           newq = findIntersect(sl, s′);
           if newq != NULL
               then delete(Q, newq);

findIntersect(sl, su)
    if sl и su пересекаются правее заметающей прямой (или на заметающей прямой выше текущей точки события)
        then return newq;
    else return NULL;

Анализ

Пусть n — число отрезков, 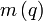$m \left(q \right)$ — число отрезков, пересекающих точку q. Тогда время на инициализацию Q равно 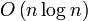$O \left(n \log n \right)$, на инициализацию T — 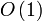$O \left(1 \right)$. На поиск всех отрезков, проходящих через точку q и обновление Q, требуется 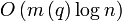$O \left(m \left(q \right) \log n \right)$ времени. На обновление T также 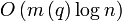$O \left(m \left(q \right) \log n \right)$ времени. Суммарно: 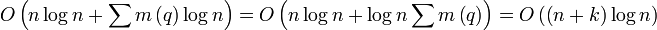$O \left(n \log n + \sum m \left(q \right) \log n \right) = O \left(n \log n + \log n \sum m \left(q \right) \right) = O \left( \left(n+k \right) \log n \right)$, где k — число точек пересечения $\left( \sum m \left(q \right) = O \left(n+k \right) \right)$. $k = O \left(n^2 \right)$.

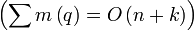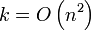Память 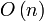$O \left(n \right)$, благодаря тому, что удаляются точки пересечения отрезков, которые перестали быть соседними, иначе было бы 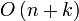$O \left(n + k \right)$, где $k = O \left(n^2 \right)$.

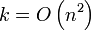Литература

• Mark de Berg, Marc van Kreveld, Mark Overmars, Otfried Schwarzkopf. Computational Geometry: Algorithms and Applications. — Springer, 2000. — С. 368.
• Прапарата Ф., Шеймос М. Вычислительная геометрия: Введение = Computational Geometry An introduction. — М.: Мир, 1989. — С. 478.
• Ласло М. Вычислительная геометрия и компьютерная графика на C++. — М.: БИНОМ, 1997. — С. 304.
• Т. Кормен, Ч. Лейзерсон, Р.Ривест, К.Штайн Алгоритмы. Построение и анализ. = Introduction to Algorithms. — 2-e изд. — “Вильямс”, 2005. — С. 1296.

Ссылки

• Визуализатор — частный случай (алгоритм Шеймоса — Гоя, 1976 (определение наличия пересекающихся отрезков)).