- Теорема о бабочке
-
Теорема о бабочке является классической теоремой планиметрии. Опубликована в 1815 году в английском мужском журнале «Gentleman's Diary» (англ.). Её авторство приписывают английскому математику Уильяму Джорджу Горнеру. Сформулировать её можно следующим образом:
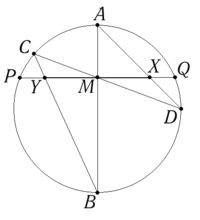
Пусть через точку М, являющуюся серединой хорды PQ некоторой окружности, проведены две произвольные хорды АВ и CD той же окружности. Пусть хорды AD и ВС пересекают хорду PQ в точках X и Y. Тогда М является серединой отрезка XY.
Содержание
О доказательствах
Теорема о бабочке имеет большое число различных доказательств, как в рамках элементарной геометрии, так и использующих методы, выходящие за её пределы (например, средства проективной геометрии).
- При помощи проецирования двойных отношений: Рассмотрим двойное отношение точек
 , и спроецируем его на окружность из точки
, и спроецируем его на окружность из точки  . Точки
. Точки  и
и  перейдут сами в себя, так как принадлежат окружности, а точки
перейдут сами в себя, так как принадлежат окружности, а точки  и
и  перейдут в точки
перейдут в точки  и
и  соответственно. Получаем
соответственно. Получаем  (последнее следует трактовать как двойное отношение точек на комплексной плоскости). Проецируем обратно на прямую
(последнее следует трактовать как двойное отношение точек на комплексной плоскости). Проецируем обратно на прямую  с центром в точке
с центром в точке  , получаем
, получаем  . Распишем двойное отношение по определению, получим необходимое равенство.
. Распишем двойное отношение по определению, получим необходимое равенство.
Вариации и обобщения
Пусть на окружности дана хорда AB, на ней — точки M и N, причём AM = BN. Через точки M и N проведены хорды PQ и RS, соответственно. Прямые QS и RP пересекают хорду AB в точках K и L. Доказать, что AK = BL.
Ссылки
- Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
- Ченцов Н. Н., Шклярский Д. О., Яглом И. М. Избранные задачи и теоремы элементарной математики. Геометрия (планиметрия). — М.: Гостехиздат, 1952.
Примечания
- ↑ В. Ю. Протасов, В. М. Тихомиров. Геометрические шедевры И. Ф. Шарыгина. В книге «Геометрические олимпиады имени И. Ф. Шарыгина», стр. 146
Категории:- Планиметрия
- Теоремы
- При помощи проецирования двойных отношений: Рассмотрим двойное отношение точек
Wikimedia Foundation. 2010.