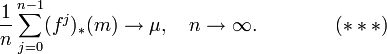- Мера Синая — Рюэлля — Боуэна
-
Мера Синая — Рюэлля — Боуэна
Мера Синая — Рюэлля — Боуэна, или SRB-мера — мера на фазовом пространстве динамической системы, к которой стремится распределение траекторий типичных начальных (в смысле меры Лебега) точек (возможно, из какой-либо области). При этом множество точек, для которых происходит такое стремление, называется бассейном притяжения этой меры.
Понятие названо в честь Я. Г. Синая, Д. Рюэлля и Р. Боуэна, в работах которых оно было введено.
Определения
Более точно, имеется два неэквивалентных понятия: определение меры Синая-Рюэля-Боуэна, связанное с итерациями типичных точек («наблюдаемая мера»), и его модификация, связанная с итерациями абсолютно непрерывных мер («естественная мера»).
Определение 1. Мера μ называется (наблюдаемой) мерой Синая-Рюэлля-Боуэна, если для множества начальных точек x положительной меры Лебега распределение орбит сходится к μ:
Эквивалентным образом это определение может быть сформулировано в терминах временных средних:
Определение 1'. Мера μ называется (наблюдаемой) мерой Синая-Рюэлля-Боуэна, если для некоторого множества M положительной меры Лебега временные средние любой непрерывной функции
 на M сходятся почти всюду к её интегралу по мере μ
на M сходятся почти всюду к её интегралу по мере μВ случае естественной меры рассматриваются итерации не атомарной начальной меры (или, что то же самое, распределение индивидуальной орбиты), а усреднение абсолютно непрерывных начальных мер:
Определение 2. Мера μ называется (естественной) мерой Синая-Рюэлля-Боуэна, если для некоторого множества M положительной меры Лебега для любой абсолютно непрерывной начальной меры m её временные средние сходятся почти всюду мере μ:
См. также
Литература
- Я.Г.Синай, Гиббсовские меры в эргодической теории, Успехи Математических Наук, 27:4 (1972), 21--69.
- R. Bowen. Equilibrium states and ergodic theory of Anosov diffeomorphisms. Springer Lecture Notes in Math. 470 (1975).
- D. Ruelle. A measure associated with Axiom A attractors. Amer. J. Math., 98 (1976), pp. 619--654.
- M. Blank, L. Bunimovich. Multicomponent dynamical systems: SRB measures and phase transitions. Nonlinearity, 16 (2003), pp. 387--401.
Wikimedia Foundation. 2010.
Мера Синая — Рюэлля Боуэна, или SRB мера мера на фазовом пространстве динамической системы, к которой стремится распределение траекторий типичных начальных (в смысле меры Лебега) точек (возможно, из какой либо области). При этом множество точек, для… … Википедия
Аттрактор — У этого термина существуют и другие значения, см. Великий аттрактор. Визуальное отображение странного аттрактора Аттрактор (англ. … Википедия
Теорема Крылова — Боголюбова — В теории динамических систем под теоремами Крылова Боголюбова понимаются две теоремы, утверждающие существование инвариантных мер у «хороших» отображений, определённых на «хороших» пространствах. Теоремы доказаны математиком Н. М. Крыловым и… … Википедия
Теорема Крылова — В теории динамических систем под теоремами Крылова Боголюбова понимаются две теоремы, утверждающие существование инвариантных мер у «хороших» отображений, определённых на «хороших» пространствах. Теоремы доказаны математиком… … Википедия

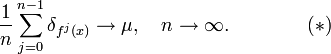
![\frac{1}{n} \sum_{j=0}^{n-1} \varphi(f^j(x)) \xrightarrow[n\to\infty]{\text{a.e. in} \,\, M} \int \varphi \, d\mu. \qquad \qquad (**)](http://dic.academic.ru/pictures/wiki/files/97/a545a36348831c2dde443abc7700d78c.png)