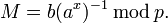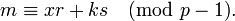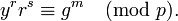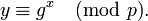Эль-гамаль

Схема Эль-Гамаля (Elgamal) — криптосистема, предложенная в 1984 году. Схема Эль-Гамаля лежит в основе стандартов электронной цифровой подписи в США и России.

Генерация ключей

1. Генерируется случайное простое число p длины n.
2. Выбирается произвольное целое число g, являющееся первообразным корнем по модулю p.
3. Выбирается случайное число x из интервала (1,p), взаимно простое с p-1.
4. Вычисляется y = g^xmod p.
5. Открытым ключом является тройка (p,g,y), закрытым ключом — число x.

Работа в режиме шифрования

Шифрование

Сообщение М шифруется так:

1. Выбирается случайное секретное число k, взаимно простое с p − 1.
2. Вычисляется a = g^kmod p, b = y^kMmod p, где M — исходное сообщение.
3. Пара чисел (a,b) является шифротекстом.

Нетрудно видеть, что длина шифротекста в схеме Эль-Гамаль длиннее исходного сообщения M вдвое.

Расшифрование

Зная закрытый ключ x, исходное сообщение можно вычислить из шифротекста (a,b) по формуле:

$M = b(a^x)^{-1}\,\bmod\,p.$

При этом нетрудно проверить, что

$a^x\equiv g^{kx}\pmod{p}$ и $\frac{b}{a^x}\equiv \frac{y^kM}{a^x}\equiv \frac{g^{xk}M}{g^{xk}}\equiv M \pmod{p}$.

Работа в режиме подписи

При работе в режиме подписи предполагается наличие фиксированной хеш-функции h(), значения которой лежат в интервале (1,p − 1).

Подпись сообщений

Для подписи сообщения M выполняются следующие операции:

1. Вычисляется дайджест сообщения M: m = h(M).
2. Выбирается случайное число 1 < k < p − 1 взаимно простое с p-1 и вычисляется $r = g^k\,\bmod\,p.$
3. С помощью расширенного алгоритма Евклида вычисляется число s, удовлетворяющее сравнению:

   $m \equiv xr + ks\pmod{p-1}.$

4. Подписью сообщения M является пара (r,s).

Проверка подписи

Зная открытый ключ (p,g,y), подпись (r,s) сообщения M проверяется следующим образом:

1. Проверяется выполнимость условий: 0 < r < p и 0 < s < p − 1. Если хотя бы одно из них не выполняется, то подпись считается неверной.
2. Вычисляется дайджест m = h(M).
3. Подпись считается верной, если выполняется сравнение:

   $y^r r^s \equiv g^m \pmod{p}.$

Криптостойкость

Криптостойкость данной схемы основана на вычислительной сложности проблемы дискретного логарифмирования, где по известным p, g и y требуется вычислить х, удовлетворяющий сравнению:

$y \equiv g^x \pmod{p}.$

Криптографические алгоритмы с парой открытый/закрытый ключ

DSA • Схема Эль-Гамаля • ГОСТ Р 34.10-2001