Электрические цепи

Электрические цепи

Электрической цепью называют совокупность соединенных друг с другом источников электрической энергии и нагрузок, по которым может протекать электрический ток.

Изображение электрической цепи с помощью условных знаков называют электрической схемой (рисунок 1).

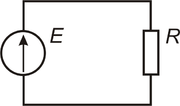Рисунок 1 — Условное обозначение электрической цепи
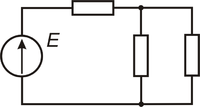Рисунок 2 — Разветвленная цепь


Содержание

Неразветвленные и разветвленные электрические цепи

Электрические цепи подразделяют на неразветвленные и разветвленные. На рисунке 1 представлена схема простейшей неразветвленной цепи. Во всех элементах ее течет один и тот же ток. Простейшая разветвленная цепь изображена на рисунке 2. В ней имеются три ветви и два узла. В каждой ветви течет свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами. В свою очередь узел есть точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рисунок 2), то в этом месте есть электрическое соединение двух линий, в противном случае его нет. Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым узлом.

Линейные и нелинейные электрические цепи

Под нелинейными электрическими цепями понимают электрические цепи, содержащие элементы с нелинейными вольт-амперными, вебер-амперными или кулон-вольтными характеристиками. Если цепь содержит хотя бы один такой элемент и изображающаяся точка в процессе работы перемещается по существенно нелинейному участку характеристики этого элемента, то она принадлежит к рассматриваемому классу цепей.

Если же в цепи нет ни одного элемента с нелинейной характеристикой, то такая цепь — линейная.

См. также

Литература

  • Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов.— 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6
  • Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Гардарики, 2002. — 638 с. — ISBN 5-8297-0026-3

Wikimedia Foundation. 2010.

Игры ⚽ Поможем написать реферат

Полезное


Смотреть что такое "Электрические цепи" в других словарях:

  • ЭЛЕКТРИЧЕСКИЕ ЦЕПИ — совокупности соединенных определенным образом элементов и устройств, образующих путь для прохождения электрического тока. Теория цепей раздел теоретической электротехники, в котором рассматриваются математические методы вычисления электрических… …   Энциклопедия Кольера

  • Электрические цепи связанные — электрические цепи, процессы в которых влияют друг на друга посредством общего магнитного поля или общего электрического поля... Источник: ЭЛЕКТРОТЕХНИКА . ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ПОНЯТИЙ. ГОСТ Р 52002 2003 (утв. Постановлением… …   Официальная терминология

  • связанные электрические цепи — Электрические цепи, процессы в которых влияют друг на друга посредством общего магнитного поля или общего электрического поля. [ГОСТ Р 52002 2003] Тематики электротехника, основные понятия …   Справочник технического переводчика

  • связанные электрические цепи — 139 связанные электрические цепи Электрические цепи, процессы в которых влияют друг на друга посредством общего магнитного поля или общего электрического поля Источник: ГОСТ Р 52002 2003: Электротехника. Термины и определения основных понятий …   Словарь-справочник терминов нормативно-технической документации

  • оборудование, содержащее электрические цепи с ограниченной энергией «nL» — оборудование, содержащее электрические цепи с ограниченной энергией «nL» Электрооборудование, все цепи и компоненты которого выполнены в соответствии с требованиями к электрическим цепям с ограниченной энергией. [ГОСТ Р МЭК 60050 426… …   Справочник технического переводчика

  • Связанное электрооборудование. Связанные электрические цепи — 17. Связанное электрооборудование. Связанные электрические цепи Электрооборудование или его цепи, которые при нормальном или аварийном режиме работы не отделены гальванически от искробезопасных цепей Источник …   Словарь-справочник терминов нормативно-технической документации

  • Связанные электрические цепи — 1. Электрические цепи, процессы в которых влияют друг на друга посредством общего магнитного поля или общего электрического поля Употребляется в документе: ГОСТ Р 52002 2003 Электротехника. Термины и определения основных понятий …   Телекоммуникационный словарь

  • цепи оперативного постоянного тока — электрические цепи, обеспечивающие возможность функционирования систем управления, защиты, контроля и регулирования основного оборудования электростанций, подстанций, устройств сигнализации и связи [Специальный технический регламент «О… …   Справочник технического переводчика

  • оборудование, содержащее электрические цепи с ограниченной энергией nL — energy limited apparatus nL Электрооборудование, все цепи и компоненты которого выполнены в соответствии с требованиями к электрическим цепям с ограниченной энергией …   Электротехнический словарь

  • ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ — электромагнитные колебания в квазистационарных цепях, размеры к рых малы по сравнению с длиной эл. магн. волны. Это позволяет не учитывать волнового характера процессов и описывать их как колебания электрич. зарядов Q (в ёмкостных элементах цепи) …   Физическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»