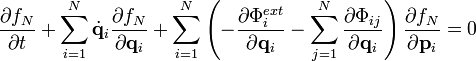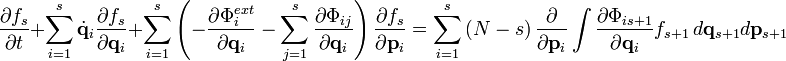- Цепочка ББГКИ
-
Цепочка уравнений Боголюбова (цепочка ББГКИ, ББГКИ иерархия, цепочка уравнений Боголюбова — Борна — Грина — Кирквуда — Ивона) — система уравнений эволюции системы, состоящей из большого числа тождественных взаимодействующих частиц, заключенных в некотором объеме V. Последовательность уравнений ББГКИ выражает эволюцию s-частичной функции распределения через (s+1)-частичную функцию распределения. Названа в честь Боголюбова, Борна, Грина, Кирквуда (англ. John Gamble Kirkwood) и Ивона (Yvon).
Содержание
Формулировка
Рассмотрим систему из N частиц с парным взаимодействием, находящуюся во внешнем поле. Пусть
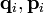 — обобщенные координаты и импульсы i-ой частицы,
— обобщенные координаты и импульсы i-ой частицы, 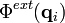 — потенциал взаимодействия с внешнем полем,
— потенциал взаимодействия с внешнем полем, 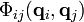 — потенциал (парного) взаимодействия частиц. Функция распределения полной системы
— потенциал (парного) взаимодействия частиц. Функция распределения полной системы 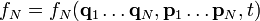 удовлетворяет уравнению Лиувилля
удовлетворяет уравнению ЛиувилляРассматриваемая цепочка уравнений получается последовательным интегрированием уравнения Лиувилля по части переменных. В результате уравнение для s-частичной функции распределения
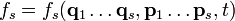 имеет вид:
имеет вид:Применение
Полученная цепочка зацепляющихся уравнений эквивалентна исходному уравнению Лиувилля и тем самым не описывает необратимость. К тому же, сложность её решения совпадает со сложностью решения уравнения Лиувилля. Однако при её обрыве и некоторых дополнительных предположениях симметричность по времени исчезает, как например при получении из цепочки ББГКИ классических[1] и квантовых[2] кинетических уравнений, и в частности, уравнения Больцмана. Подобные упрощения делают ББГКИ иерархию отправной точкой для многих кинетических теорий.
Примечания
- ↑ Боголюбов Н. Н. Кинетические уравнения // Журнал экспериментальной и теоретической физики. — 1946. — Т. 16 (8). — С. 691—702.
- ↑ Боголюбов Н. Н., Гуров К. П. Кинетические уравнения в квантовой механике // Журнал экспериментальной и теоретической физики. — 1947. — Т. 17 (7). — С. 614—628.
См. также
Литература
- Боголюбов Н. Н. Проблемы динамической теории в статистической физике. — М.: Изд-во Гостехиздат, 1946. — 120 с.
- Боголюбов Н. Н. Избранные труды по статистической физике. — М.: Изд-во МГУ, 1979.
- Боголюбов Н. Н. Собрание научных трудов: в 12-ти тт. — М.: Наука, 2006. — Т. 5: Неравновесная статистическая механика, 1939—1980. — ISBN 5020341428
- Гуров К. П. Основания кинетической теории (метод Н. Н. Боголюбова). — М.: Наука, 1966. — 352 с.
- Шелест А. В. Метод Боголюбова в динамической теории кинетических уравнений. — М.: Наука, 1990. — 159 с. — ISBN 5020140309
Wikimedia Foundation. 2010.