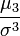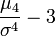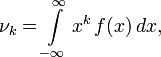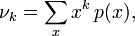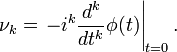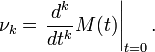Центральные моменты случайной величины
- Центральные моменты случайной величины
-
Моме́нт случа́йной величины́ — числовая характеристика распределения данной случайной величины.
Определения
Если дана случайная величина 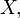 определённая на некотором вероятностном пространстве, то:
определённая на некотором вероятностном пространстве, то:
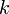 -м нача́льным моментом случайной величины
-м нача́льным моментом случайной величины 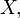 где
где 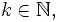 называется величина
называется величина
-
![\nu_k = \mathbb{E}\left[X^k\right],](/pictures/wiki/files/56/866b21ca204f3286c29ec780254acc89.png)
- если математическое ожидание
![\mathbb{E}[*]](/pictures/wiki/files/52/489055831bfa0b34746d216c2ba8e537.png) в правой части этого равенства определено;
в правой части этого равенства определено;
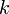 -м центра́льным моментом случайной величины
-м центра́льным моментом случайной величины 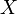 называется величина
называется величина
-
![\mu_k = \mathbb{E}\left[(X - \mathbb{E}X)^k\right],](/pictures/wiki/files/102/f2a7fc35e15b3af654fecee615fb03a5.png)
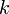 -м факториальным моментом случайной величины
-м факториальным моментом случайной величины 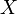 называется величина
называется величина
-
![\mu_k = \mathbb{E}\left[X(X-1)...(X-k+1)\right],](/pictures/wiki/files/97/a9ee4be4a84cec57b44f9b7de13398c0.png)
- если математическое ожидание в правой части этого равенства определено.
Замечания
- Если определены моменты
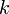 -го порядка, то определены и все моменты низших порядков
-го порядка, то определены и все моменты низших порядков 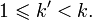
- В силу линейности математического ожидания центральные моменты могут быть выражены через начальные, и наоборот. Например:
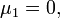
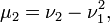
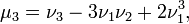
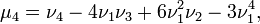 и т. д.
и т. д.
Геометрический смысл некоторых моментов
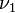 равняется математическому ожиданию случайной величины и показывает относительное расположение распределения на числовой прямой.
равняется математическому ожиданию случайной величины и показывает относительное расположение распределения на числовой прямой.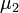 равняется дисперсии распределения
равняется дисперсии распределения 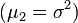 и показывает разброс распределения вокруг среднего значения.
и показывает разброс распределения вокруг среднего значения.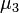 , будучи соответствующим образом нормализован, является числовой характеристикой симметрии распределения. Более точно, выражение
, будучи соответствующим образом нормализован, является числовой характеристикой симметрии распределения. Более точно, выражение
-
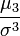
- называется коэффициентом асимметрии.
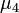 контролирует, насколько ярко выражена вершина распределения в окрестности среднего. Величина
контролирует, насколько ярко выражена вершина распределения в окрестности среднего. Величина
-
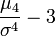
- называется коэффициентом эксцесса распределения
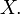
Вычисление моментов
-
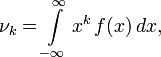
если 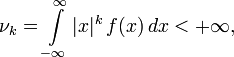
- а для дискретного распределения с функцией вероятности
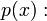
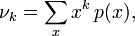
если 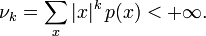
-
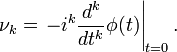
- Если распределение таково, что для него в некоторой окрестности нуля определена производящая функция моментов
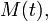 то моменты могут быть вычислены по следующей формуле:
то моменты могут быть вычислены по следующей формуле:
-
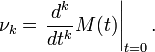
Обобщения
Можно также рассматривать нецелые значения k. Момент, рассматриваемый как функция от аргумента k, называется преобразованием Меллина.
Можно рассматривать моменты многомерной случайной величины. Тогда первый момент будет вектором той же размерности, второй — тензором второго ранга (см. матрица ковариации) над пространством той же размерности (хотя можно рассматривать и след этой матрицы, дающий скалярное обобщение дисперсии). Итд.
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Центральные моменты случайной величины" в других словарях:
Моменты случайной величины — Момент случайной величины числовая характеристика распределения данной случайной величины. Содержание 1 Определения 2 Замечания … Википедия
Центральная — Центральный прилагательное к существительному «центр». Входит в состав многих сложных терминов. Не следеут путать его с термином «централ». Содержание 1 Географические названия 1.1 Регионы мира 1.2 Государства … Википедия
Центрально — Центральный прилагательное к существительному «центр». Входит в состав многих сложных терминов. Не следеут путать его с термином «централ». Содержание 1 Географические названия 1.1 Регионы мира 1.2 Государства … Википедия
Центральный (Нижегородская область) — Центральный прилагательное к существительному «центр». Входит в состав многих сложных терминов. Не следеут путать его с термином «централ». Содержание 1 Географические названия 1.1 Регионы мира 1.2 Государства … Википедия
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
МНОГОМЕРНОЕ РАСПРЕДЕЛЕНИЕ — распределение вероятностей на алгебре борелевских множеств s мерного евклидова пространства . О М. р. обычно говорят как о распределении многомерной случайной величины или случайного вектора , понимая под этим совместное распределение… … Математическая энциклопедия
ЭКСЦЕССА КОЭФФИЦИЕНТ — эксцесс, скалярная характеристика островершинности графика плотности вероятности унимодального распределения, к рую используют в качестве нек рой меры отклонения рассматриваемого распределения от нормального. Э. к. определяется по формуле где… … Математическая энциклопедия
ЭДЖВОРТА РЯД — ряд, определяемый выражением Здесь f(x) плотность распределения случайной величины независимы и одинаково распределены), плотность стандартного нормального распределения, Коэффициенты bk,k+2l не зависят от пи представляют собой многочлены… … Математическая энциклопедия
ГРАМА - ШАРЛЬЕ РЯД — ряд, определяемый выражением или где х нормированное значение случайной величины. Ряд (1) наз. Г. Ш. р. типа А;здесь есть k я производная от , к рую можно представить в виде где многочлены Чеб … Математическая энциклопедия
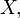 определённая на некотором вероятностном пространстве, то:
определённая на некотором вероятностном пространстве, то: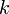 -м нача́льным моментом случайной величины
-м нача́льным моментом случайной величины 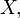 где
где 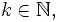 называется величина
называется величина![\mathbb{E}[*]](/pictures/wiki/files/52/489055831bfa0b34746d216c2ba8e537.png) в правой части этого равенства определено;
в правой части этого равенства определено;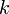 -м центра́льным моментом случайной величины
-м центра́льным моментом случайной величины 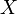 называется величина
называется величина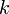 -м факториальным моментом случайной величины
-м факториальным моментом случайной величины 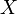 называется величина
называется величина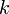 -го порядка, то определены и все моменты низших порядков
-го порядка, то определены и все моменты низших порядков 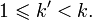
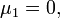
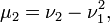
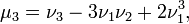
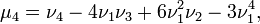 и т. д.
и т. д.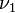 равняется математическому ожиданию случайной величины и показывает относительное расположение распределения на числовой прямой.
равняется математическому ожиданию случайной величины и показывает относительное расположение распределения на числовой прямой.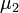 равняется дисперсии распределения
равняется дисперсии распределения 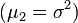 и показывает разброс распределения вокруг среднего значения.
и показывает разброс распределения вокруг среднего значения.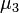 , будучи соответствующим образом нормализован, является числовой характеристикой симметрии распределения. Более точно, выражение
, будучи соответствующим образом нормализован, является числовой характеристикой симметрии распределения. Более точно, выражение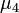 контролирует, насколько ярко выражена вершина распределения в окрестности среднего. Величина
контролирует, насколько ярко выражена вершина распределения в окрестности среднего. Величина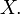
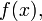 имеем:
имеем: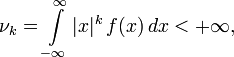
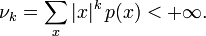
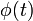 :
: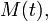 то моменты могут быть вычислены по следующей формуле:
то моменты могут быть вычислены по следующей формуле:
![\nu_k = \mathbb{E}\left[X^k\right],](/pictures/wiki/files/56/866b21ca204f3286c29ec780254acc89.png)
![\mu_k = \mathbb{E}\left[(X - \mathbb{E}X)^k\right],](/pictures/wiki/files/102/f2a7fc35e15b3af654fecee615fb03a5.png)
![\mu_k = \mathbb{E}\left[X(X-1)...(X-k+1)\right],](/pictures/wiki/files/97/a9ee4be4a84cec57b44f9b7de13398c0.png)