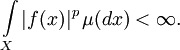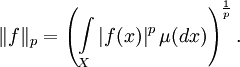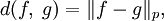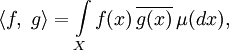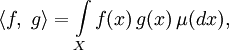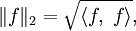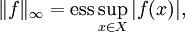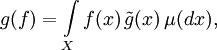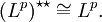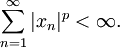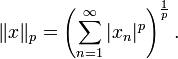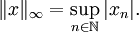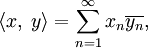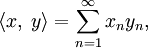- Пространство Lp
-
Пространство Lp
Для термина «Lp» см. другие значения.Пространства Lp (читается «эль-пэ») — это пространства измеримых функций таких, что их p-я степень интегрируема, где
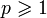 .
.Lp — важнейший класс банаховых пространств. В дополнение, L2 (читается «эль-два») — классический пример гильбертова пространства.
Содержание
Построение пространства Lp
Определение 1. Пусть дано пространство с мерой
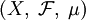 . Фиксируем
. Фиксируем 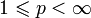 и рассмотрим множество измеримых функций, определенных на этом пространстве, таких что
и рассмотрим множество измеримых функций, определенных на этом пространстве, таких чтоОбозначим это множество
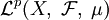 или просто
или просто  .
.Теорема 1. Пространство
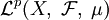 линейно. Доказательство следует из элементарных свойств интеграла Лебега, а также неравенства Минковского.
линейно. Доказательство следует из элементарных свойств интеграла Лебега, а также неравенства Минковского.На этом линейном пространстве можно ввести полунорму:
Неотрицательность и однородность следуют напрямую из свойств интеграла Лебега, а неравенство Минковского является неравенством треугольника для этой полунормы.
Замечание 1. Введённая таким образом полунорма не является нормой, ибо если f(x) = 0 почти всюду, то
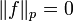 , что противоречит требованиям к норме. Чтобы превратить пространство с полунормой в пространство с нормой, необходимо «отождествить» функции, различающиеся между собой лишь на множестве меры нуль.
, что противоречит требованиям к норме. Чтобы превратить пространство с полунормой в пространство с нормой, необходимо «отождествить» функции, различающиеся между собой лишь на множестве меры нуль.Определение 2. Введём на
 отношение эквивалентности. Будем говорить, что
отношение эквивалентности. Будем говорить, что 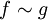 , если f(x) = g(x) почти всюду.
, если f(x) = g(x) почти всюду.Это отношение разбивает пространство
 на непересекающиеся классы эквивалентности, причём полунормы любых двух представителей одного и того же класса совпадают.
на непересекающиеся классы эквивалентности, причём полунормы любых двух представителей одного и того же класса совпадают.Тогда на построенном факторпространстве (то есть семействе классов эквивалентности)
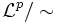 можно ввести норму равную полунорме любого представителя данного класса. По определению, все аксиомы полунормы сохранятся, и вдобавок в силу изложенного построения оказывается выполненной и положительная определённость.
можно ввести норму равную полунорме любого представителя данного класса. По определению, все аксиомы полунормы сохранятся, и вдобавок в силу изложенного построения оказывается выполненной и положительная определённость.Определение 3. Факторпространство
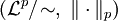 с построенной на нём нормой называется пространством
с построенной на нём нормой называется пространством 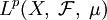 или просто Lp.
или просто Lp.Замечание 2. Чаще всего вышеизложенное построение имеют в виду, но не упоминают явно. Тогда элементами Lp называют не классы эквивалентности функций, а сами функции, «определённые с точностью до меры нуль».
 Комментарий: при 0 < p < 1, Lp не образуют нормированного пространства, так как не выполняется неравенство треугольника[1], однако образуют метрическое пространства. В этих пространствах нет нетривиальных линейных непрерывных операторов.
Комментарий: при 0 < p < 1, Lp не образуют нормированного пространства, так как не выполняется неравенство треугольника[1], однако образуют метрическое пространства. В этих пространствах нет нетривиальных линейных непрерывных операторов.Полнота пространства Lp
Введённая выше норма вместе с линейной структурой порождает метрику
а следовательно и понятие сходимости.
Определение 3. Пусть есть последовательность функций
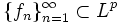 . Тогда эта последовательность сходится к функции
. Тогда эта последовательность сходится к функции 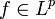 , если
, если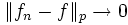 при
при 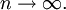
Теорема 2. Пространство Lp полно, то есть любая фундаментальная последовательность в Lp сходится к элементу этого же пространства. Таким образом Lp — банахово пространство.
Пространство L²
В случае p = 2 введённая выше норма порождается скалярным произведением. Таким образом вместе с понятием «длины» здесь имеет смысл и понятие «угла», а следовательно и смежные понятия, таких как ортогональность, проекция и пр.
Определение 4. Введём на пространстве L2 скалярное произведение следующим образом:
в случае, если рассматриваемые функции комплекснозначные, или
если они вещественные. Тогда, очевидно,
то есть норма порождается скалярным произведением. Используя это вместе с результатом о полноте любого Lp, заключаем, что имеет место
Теорема 3. Пространство L2 гильбертово.
Пространство L∞
Рассмотрим пространство
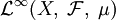 измеримых функций, ограниченных почти всюду. Отождествив между собой функции, различающиеся лишь на множестве меры нуль, и, положив по определению
измеримых функций, ограниченных почти всюду. Отождествив между собой функции, различающиеся лишь на множестве меры нуль, и, положив по определениюполучается полное нормированное, то есть банахово пространство.
Метрика, порождаемая этой нормой, называется равномерной. Так же называется и сходимость, порождённая такой метрикой:
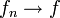 в
в 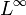 , если
, если 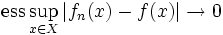 при
при 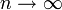 .
.
Свойства пространств Lp
- Сходимость функций почти всюду не влечёт сходимость в пространстве Lp. Пусть fn(x) = n1 / p при
![x\in(0,1/n]](http://dic.academic.ru/pictures/wiki/files/56/8018eb9ad8f3030d92b9ed8b9db1e65f.png) и fn(x) = 0 при
и fn(x) = 0 при ![x\in(1/n,1]](http://dic.academic.ru/pictures/wiki/files/51/3c98f14e255bdd19a3274d7d7b6a774d.png) ,
, 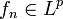 . Тогда
. Тогда  почти всюду. Но
почти всюду. Но 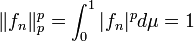 . Обратное также неверно.
. Обратное также неверно. - Если
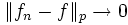 при
при 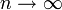 , то существует подпоследовательность
, то существует подпоследовательность 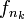 , такая что
, такая что 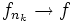 почти всюду.
почти всюду. - Lp функции на числовой прямой могут быть приближены гладкими функциями. Пусть
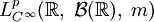 — подмножество
— подмножество 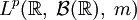 , состоящее из бесконечно гладких функций. Тогда
, состоящее из бесконечно гладких функций. Тогда 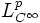 всюду плотно в Lp.
всюду плотно в Lp. 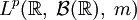 — сепарабельно.
— сепарабельно.- Если μ — конечная мера, например, вероятность, и
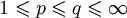 , то
, то 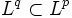 . В частности,
. В частности, 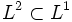 , то есть случайная величина с конечным вторым моментом имеет конечный первый момент.
, то есть случайная величина с конечным вторым моментом имеет конечный первый момент.
Пространства сопряжённые к Lp
Пространством
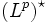 называется пространство линейных функционалов на Lp. Это пространство сопряжённое к Lp (копространство).
называется пространство линейных функционалов на Lp. Это пространство сопряжённое к Lp (копространство).Теорема 4. Если
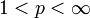 , то
, то 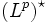 изоморфно Lq (пишем
изоморфно Lq (пишем 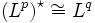 ), где 1 / p + 1 / q = 1. Любой линейный функционал на Lp имеет вид:
), где 1 / p + 1 / q = 1. Любой линейный функционал на Lp имеет вид:где
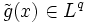 .
.В силу симметрии уравнения 1 / p + 1 / q = 1, само пространство Lp дуально (с точностью до изоморфизма) к Lq, а следовательно:
Этот результат справедлив и для случая p = 1, то есть
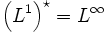 . Однако,
. Однако, 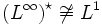 и, в частности,
и, в частности, 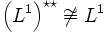 .
.Пространства lp, 1 ≤ p ≤ ∞
Пусть
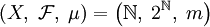 , где m — счётная мера на
, где m — счётная мера на 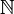 , то есть
, то есть 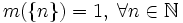 . Тогда если
. Тогда если 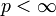 , то пространство
, то пространство 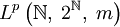 представляет собой семейство последовательностей
представляет собой семейство последовательностей 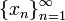 , таких что
, таких чтоСоответственно, норма на этом пространстве задаётся
Получившееся нормированное пространство обозначается lp.
Если
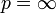 , то мы рассматриваем пространство ограниченных последовательностей с нормой
, то мы рассматриваем пространство ограниченных последовательностей с нормойПолучившееся пространство называется
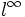 . Оно является примером не сепарабельного пространства.
. Оно является примером не сепарабельного пространства.Как и в общем случае, положив p = 2, мы получаем гильбертово пространство l2, чья норма порождена скалярным произведением
если последовательности комплекснозначные, и
если они вещественны.
Пространство, дуальное к lp, где
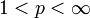 изоморфно lq, 1 / p + 1 / q = 1. Для
изоморфно lq, 1 / p + 1 / q = 1. Для 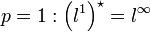 . Однако,
. Однако, 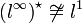 .
.Примечания
- ↑ Точнее, выполняется обратное неравенство треугольника:при 0 < p < 1
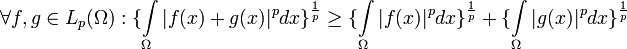
Литература
- Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. — изд. четвёртое, переработанное. — М.: Наука, 1976. — 544 с.
- Треногин В. А. Функциональный анализ. — М.: Наука, 1980. — 495 с.
Wikimedia Foundation. 2010.
ПРОСТРАНСТВО — фундаментальное (наряду с временем) понятие человеческого мышления, отображающее множественный характер существования мира, его неоднородность. Множество предметов, объектов, данных в человеческом восприятии одновременно, формирует сложный… … Философская энциклопедия
ПРОСТРАНСТВО — П., будучи одним из важнейших элементов мифопоэтической архаичной модели мира, осмысливалось в рамках этой модели совершенно отлично от того, как оно представляется современному человечеству под воздействием научных взглядов (особенно после… … Энциклопедия мифологии
Пространство — Пространство ♦ Espace То, что остается, если убрать все; пустота, но пустота в трех измерениях. Ясно, что понятие пространства – абстракция (если мы действительно уберем все, то не останется вообще ничего, и это будет уже не пространство, а… … Философский словарь Спонвиля
ПРОСТРАНСТВО — в математике множество объектов, между которыми установлены отношения, сходные по своей структуре с обычными пространственными отношениями типа окрестности, расстояния и т. д. Исторически первое и важнейшее математическое пространство евклидово… … Большой Энциклопедический словарь
пространство — См. промежуток... Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. пространство место, промежуток; площадь, участок, зона, район, область; окно, протяженность, прогалина, гаммада,… … Словарь синонимов
пространство — ПРОСТРАНСТВО фундаментальное понятие повседневной жизни и научного знания. Его обычное применение непроблематично в отличие от его теоретической экспликации, поскольку последнее связано с множеством других понятий и предполагает… … Энциклопедия эпистемологии и философии науки
ПРОСТРАНСТВО — ПРОСТРАНСТВО, объективная реальность, форма существования материи, характеризующаяся протяженностью и объемом. В реальном мире мы имеем дело с безграничным трехмерным пространством, в котором расположены объекты. В математике пространством… … Научно-технический энциклопедический словарь
пространство — пространство: восприятие восприятие пространства пространство: восприятие: нарушение … Большая психологическая энциклопедия
ПРОСТРАНСТВО — культуры важнейший аспект модели мира, характеристика протяженности, структурности, сосуществования, взаимодействия, координации элементов отд. культуры и соответствующих отношений между культурами, а также смысловой… … Энциклопедия культурологии
ПРОСТРАНСТВО — ПРОСТРАНСТВО, пространства, ср. 1. Состояние материи, характеризующееся наличием протяженности и объема. Пространство и время основные формы существования материи. 2. Промежуток между чем нибудь; место, способное вместить что нибудь. Свободное… … Толковый словарь Ушакова