- Аксиоматика вещественных чисел
-
Аксиоматика вещественных чисел
Аксиома́тика веще́ственных чи́сел — система аксиом, один из способов определения вещественных (действительных) чисел.
Далее символ
 обозначает логическое «и».
обозначает логическое «и».Содержание
Аксиомы сложения
На множестве вещественных чисел, обозначаемом через
 (так называемую R рубленую), введена операция сложения («+»), то есть каждой паре элементов (x,y) из множества вещественных чисел ставится в соответствие элемент x + y из этого же множества, называемый суммой x и y.
(так называемую R рубленую), введена операция сложения («+»), то есть каждой паре элементов (x,y) из множества вещественных чисел ставится в соответствие элемент x + y из этого же множества, называемый суммой x и y.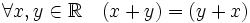 (коммутативность сложения);
(коммутативность сложения);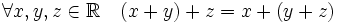 (ассоциативность сложения);
(ассоциативность сложения);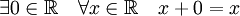 (существование нейтрального элемента по сложению — нуля);
(существование нейтрального элемента по сложению — нуля);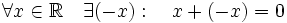 (существование противоположного элемента).
(существование противоположного элемента).
Аксиомы умножения
На
 введена операция умножения («·»), то есть каждой паре элементов (x,y) из множества вещественных чисел ставится в соответствие элемент
введена операция умножения («·»), то есть каждой паре элементов (x,y) из множества вещественных чисел ставится в соответствие элемент 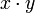 (или, сокращённо, xy) из этого же множества, называемый произведением x и y.
(или, сокращённо, xy) из этого же множества, называемый произведением x и y.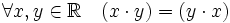 (коммутативность умножения);
(коммутативность умножения);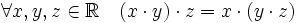 (ассоциативность умножения);
(ассоциативность умножения);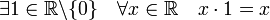 (существование нейтрального элемента по умножению — единицы);
(существование нейтрального элемента по умножению — единицы);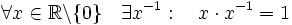 (существование обратного элемента).
(существование обратного элемента).
Связь сложения и умножения
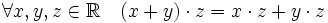 (дистрибутивность относительно сложения).
(дистрибутивность относительно сложения).
Аксиомы порядка
На
 задано отношение порядка «
задано отношение порядка «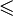 » (меньше или равно), то есть для любой пары x, y из
» (меньше или равно), то есть для любой пары x, y из  выполняется хотя бы одно из условий
выполняется хотя бы одно из условий 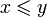 или
или 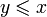 .
.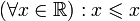 (рефлексивность порядка);
(рефлексивность порядка);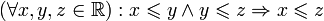 (транзитивность порядка);
(транзитивность порядка);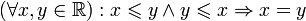 (антисимметричность порядка).
(антисимметричность порядка).
Связь отношения порядка и сложения
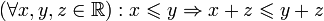 .
.Связь отношения порядка и умножения
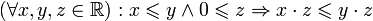 .
.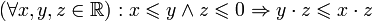
Аксиома непрерывности
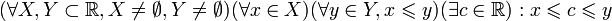 .
.Комментарий
Эта аксиома означает, что если X и Y — два непустых множества вещественных чисел такие, что любой элемент из X не превосходит любого элемента из Y, то между этими множествами можно вставить вещественное число. Для рациональных чисел эта аксиома не выполняется; классический пример: рассмотрим положительные рациональные числа и отнесём к множеству X те числа, квадрат которых меньше 2, а прочие — к Y. Тогда между X и Y нельзя вставить рациональное число (
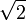 не является рациональным числом).
не является рациональным числом).Эта ключевая аксиома обеспечивает плотность
 и тем самым делает возможным построение математического анализа. Для иллюстрации её важности укажем на два фундаментальных следствия из неё.
и тем самым делает возможным построение математического анализа. Для иллюстрации её важности укажем на два фундаментальных следствия из неё.- Каждая неубывающая ограниченная сверху последовательность в
 имеет предел.
имеет предел. - Если непрерывное отображение f(x) на концах интервала имеет значения разного знака, то уравнение f(x) = 0 внутри интервала имеет вещественное решение.
Следствия аксиом
Непосредственно из аксиом следуют некоторые важные свойства вещественных чисел, например,
- единственность нуля,
- единственность противоположного и обратного элементов.
Литература
- Зорич В. А. Математический анализ. Том I. М.: Фазис, 1997, глава 2.
См. также
Ссылки
Wikimedia Foundation. 2010.
