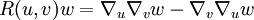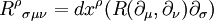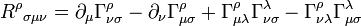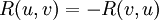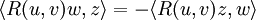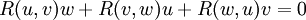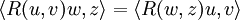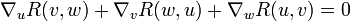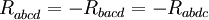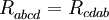Риманова кривизна

В дифференциальной геометрии тензор кривизны Римана представляет собой стандартный способ выражения кривизны римановых многообразий, а в общем случае — произвольных многообразий аффинной связности, без кручения или с кручением. Назван в честь Бернхарда Римана.

Определение

Тензор кривизны R(u,v) определяется как линейное преобразование касательного пространства в каждой точке многообразия, которое характеризует изменение вектора, параллельно перенесённого по бесконечно малому замкнутому параллелограмму, натянутому на векторы u,v. Тензор кривизны выражается через связность Леви-Чивита, или в общем случае аффинную связность $\nabla$ (которая также называется ковариантной производной) следующим образом:

$R(u,v)w=\nabla_u\nabla_v w - \nabla_v \nabla_u w - \nabla_{[u,v]} w,$

где [u,v] — скобка Ли.

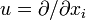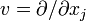Если векторные поля задаются дифференцированием по координатам, $u=\partial/\partial x_i$ и $v=\partial/\partial x_j$, и поэтому коммутируют ([u,v] = 0), формула принимает упрощённый вид

$R(u,v)w=\nabla_u\nabla_v w - \nabla_v \nabla_u w$

таким образом, тензор кривизны измеряет некоммутативность ковариантных производных.

Примечание: Некоторые авторы определяют тензор кривизны с противоположным знаком

Связанные определения

• Линейное преобразование 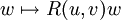$w\mapsto R(u,v)w$ называется преобразованием кривизны.
• Если u и v — два перпендикулярных единичных вектора в точке p, то выражение 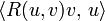$\langle R(u,v)v,\,u\rangle$ зависит только от плоскости σ в T_p которая натягивается на u и v.
  • Плоскость σ называется секционным направлением.
  • величина 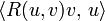$\langle R(u,v)v,\,u\rangle$ называется секционной кривизной в направлении σ, и обычно обозначается K_σ.

Компоненты тензора кривизны

В системе координат x^μ компоненты тензора кривизны определяются так:

${R^\rho}_{\sigma\mu\nu} = dx^\rho(R(\partial_{\mu},\partial_{\nu})\partial_{\sigma})$

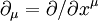где $\partial_{\mu} = \partial/\partial x^{\mu}$ — векторное поле, в каждой точке касательное к координатной линии x^μ. В терминах символов Кристоффеля :

${R^\rho}_{\sigma\mu\nu} = \partial_\mu\Gamma^\rho_{\nu\sigma} - \partial_\nu\Gamma^\rho_{\mu\sigma} + \Gamma^\rho_{\mu\lambda}\Gamma^\lambda_{\nu\sigma} - \Gamma^\rho_{\nu\lambda}\Gamma^\lambda_{\mu\sigma}$

В двумерном пространстве нетривиальной компонентой является только гауссова кривизна.

Симметрии

Тензор кривизны Римана обладает следующими свойствами симметрии:

$R(u,v)=-R(v,u)^{}_{}$

$\langle R(u,v)w,z \rangle=-\langle R(u,v)z,w \rangle^{}_{}$

$R(u,v)w+R(v,w)u+R(w,u)v=0 ^{}_{}$

Последнее тождество было открыто Риччи, хотя называется первым тождеством Бьянки или алгебраическим тождеством Бьянки.

Эти три тождества задают полный набор симметрий тензора кривизны, то есть для всякого тензора, удовлетворяющего этим соотношениям, можно найти риманово многообразие, кривизна которого описывается этим тензором. Простой комбинаторный подсчёт показывает, что тензор кривизны должен иметь n²(n² − 1) / 12 независимых компонент.

Еще одно полезное соотношение следует из этих трех тождеств:

$\langle R(u,v)w,z \rangle=\langle R(w,z)u,v \rangle^{}_{}$

Тождество Бьянки (еще называется вторым тождеством Бьянки или дифференциальным тождеством Бьянки) привлекает ковариантные производные:

$\nabla_uR(v,w)+\nabla_vR(w,u)+\nabla_w R(u,v) = 0$

В заданной системе координат в окрестности некоторой точки многообразия приведённые выше тождества в компонентах тензора кривизны могут быть записаны как:

$R_{abcd}^{}=-R_{bacd}=-R_{abdc}$

$R_{abcd}^{}=R_{cdab}$

$R_{a[bcd]}^{}=0$ (первое тождество Бьянки)

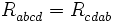$R_{abcd}^{}=R_{cdab}^{}$ (следствие (1), (2) и (3))

$R_{ab[cd;e]}^{}=0$ (второе тождество Бьянки)

где квадратные скобки обозначают симметризацию.

См. также

• Параллельное перенесение
• Метрический тензор
• Ковариантная производная
• Символы Кристоффеля