- Ресамплинг
-
 Иллюстрация эффекта наложения спектров при децимации изображения. Сверху — исходное изображение. Слева снизу — уменьшенное в два раза с фильтрацией. Справа снизу — уменьшенное в два раза без фильтрации (с наложением спектров).
Иллюстрация эффекта наложения спектров при децимации изображения. Сверху — исходное изображение. Слева снизу — уменьшенное в два раза с фильтрацией. Справа снизу — уменьшенное в два раза без фильтрации (с наложением спектров).Передискретиза́ция (англ. resampling) в обработке сигналов — изменение частоты дискретизации дискретного (чаще всего цифрового) сигнала. Алгоритмы передискретизации широко применяются при обработке звуковых сигналов, радиосигналов и изображений.
В англоязычной литературе применяются также термины downsampling для обозначения понижения частоты дискретизации и upsampling для её повышения.
Понятие передискретизации не следует смешивать с процедурой дискретизации сигнала с запасом по частоте дискретизации (англ. oversampling).
Содержание
Общие принципы
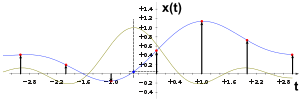 Вычисление промежуточного отсчёта дискретного сигнала с помощью идеального фильтра нижних частот. Синия кривая — исходный непрерывный сигнал, зелёная — импульсная характеристика идеального ФНЧ.
Вычисление промежуточного отсчёта дискретного сигнала с помощью идеального фильтра нижних частот. Синия кривая — исходный непрерывный сигнал, зелёная — импульсная характеристика идеального ФНЧ.Согласно теореме Котельникова любой непрерывный сигнал с финитным спектром (то есть таким спектром, что спектральные составляющие, соответствующие частотам выше некоторой частоты f0, отсутствуют) может быть представлен в виде отсчётов дискретного сигнала с частотой дискретизации fd > 2f0. При этом такое преобразование является взаимно однозначным, то есть при соблюдении условий теоремы Котельникова по дискретному сигналу можно восстановить исходный сигнал с финитным спектром без искажений.
При передискретизации отсчёты сигнала, соответствующие одной частоте дискретизации, вычисляются по имеющимся отсчётам этого же сигнала, соответствующим другой частоте дискретизации (при этом предполагается, что обе частоты дискретизации соответствуют условиям теоремы Котельникова). Идеальная передискретизация эквивалентна восстановлению непрерывного сигнала по его отсчётам с последующей дискретизацией его на новой частоте.
Точное вычисление значения исходного непрерывного сигнала в определённой точке производится следующим образом:
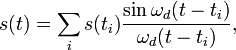
где s(ti) — i-й отсчёт сигнала, ti — момент времени, соответствующий этому отсчёту, s(t) — интерполированное значение сигнала в момент времени t.
Сложность практического применения этого выражения заключается в том, что функция
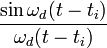 не является финитной, поэтому для вычисления значения сигнала в определённый момент времени необходимо обработать бесконечное число его отсчётов (как в прошлом, так и в будущем). В реальной жизни интерполяция осуществляется с помощью других фильтров, при этом выражение для неё принимает следующий вид:
не является финитной, поэтому для вычисления значения сигнала в определённый момент времени необходимо обработать бесконечное число его отсчётов (как в прошлом, так и в будущем). В реальной жизни интерполяция осуществляется с помощью других фильтров, при этом выражение для неё принимает следующий вид: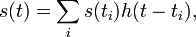
где h(t) — импульсная характеристика соответствующего восстанавливающего фильтра. Вид этого фильтра выбирается в зависимости от задачи.
Прямое вычисление новых отсчётов сигнала по вышеприведённым формулам требует значительных вычислительных ресурсов и нежелательно для приложений реального времени. Существуют важные частные случаи передискретизации, для которых вычисление новых отсчётов производится проще:
- децимация — уменьшение частоты дискретизации в целое число раз;
- интерполяция в узком смысле — увеличение частоты дискретизации в целое число раз.
При таких ограничениях становится удобным применение цифровых фильтров для передискретизации.
Передискретизация с помощью цифровых фильтров
 Иллюстрация алгоритма децимации дискретного сигнала (с коэффициентом 2). Красные точки обозначают отсчеты, сплошные линии — непрерывный сигнал, представлением которого эти отсчеты являются. Сверху — исходный сигнал. В середине — этот же сигнал после фильтрации в цифровом фильтре нижних частот. Снизу — децимированный сигнал.
Иллюстрация алгоритма децимации дискретного сигнала (с коэффициентом 2). Красные точки обозначают отсчеты, сплошные линии — непрерывный сигнал, представлением которого эти отсчеты являются. Сверху — исходный сигнал. В середине — этот же сигнал после фильтрации в цифровом фильтре нижних частот. Снизу — децимированный сигнал.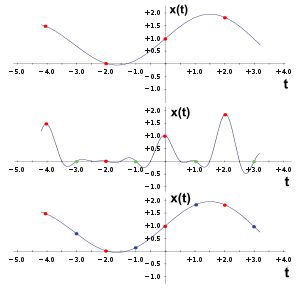 Иллюстрация алгоритма интерполяции дискретного сигнала (с коэффициентом 2). Красные точки обозначают исходные отсчеты сигнала, сплошные линии — непрерывный сигнал, представлением которого эти отсчеты являются. Сверху — исходный сигнал. В середине — этот же сигнал со вставленными нулевыми отсчётами (зеленые точки). Снизу — интерполированный сигнал (синие точки — интерполированные значения отсчётов).
Иллюстрация алгоритма интерполяции дискретного сигнала (с коэффициентом 2). Красные точки обозначают исходные отсчеты сигнала, сплошные линии — непрерывный сигнал, представлением которого эти отсчеты являются. Сверху — исходный сигнал. В середине — этот же сигнал со вставленными нулевыми отсчётами (зеленые точки). Снизу — интерполированный сигнал (синие точки — интерполированные значения отсчётов).Децимация
Децимацией называют уменьшение частоты дискретизации в целое число раз (далее N). Децимация цифрового сигнала производится в два этапа:
- Цифровая фильтрация сигнала с целью удаления высокочастотных составляющих, не удовлетворяющих условиям теоремы Котельникова для новой частоты дискретизации;
- Удаление (отбрасывание) лишних отсчетов (сохраняется каждый N-й отсчёт).
Первый этап необходим для исключения наложения спектров, природа которого аналогична наложению спектров при первоначальной дискретизации аналогового сигнала. Наложение спектров особенно заметно на тех участках сигнала, которые содержат значительные высокочастотные спектральные составляющие. Так, на приведённых в начале статьи фотографиях небо практически не подвергнулось наложению спектров, но эффект бросается в глаза, если обратить внимание на резкие переходы (такие как чёткие линии зданий и дорожной разметки).
При программной реализации алгоритма децимации «лишние» отсчёты не удаляются, а просто не вычисляются. При этом число обращений к цифровому фильтру уменьшается в N раз.
Интерполяция
Под интерполяцией в узком смысле понимают увеличение частоты дискретизации сигнала в целое число раз путем вычисления промежуточных отсчетов по уже имеющимся. Идеальная интерполяция позволяет точно восстановить значения сигнала в промежуточных отсчётах.
Стандартный алгоритм интерполяции заключается в следующем:
- вставка нулевых отсчетов на место отсчетов, которые необходимо вычислить;
- фильтрация сигнала цифровым фильтром нижних частот для того, чтобы убрать спектральные составляющие сигнала, которых заведомо не могло быть в исходном сигнале согласно теореме Котельникова.
Точность этого метода ограничивается невозможностью реализации фильтра нижних частот с идеально прямоугольной частотной характеристикой.
При программной реализации интерполяции нулевые отсчёты не участвуют в вычислении полинома, что позволяет оптимизировать процесс вычисления.
Комбинация интерполяции и децимации
Для того, чтобы изменить частоту дискретизации сигнала в
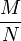 раз (M и N — целые положительные числа), можно сначала провести интерполяцию, увеличив частоту дискретизации в M раз, а затем с помощью децимации уменьшить её в N раз. Фильтрацию сигнала достаточно произвести всего один раз — между интерполяцией и децимацией.
раз (M и N — целые положительные числа), можно сначала провести интерполяцию, увеличив частоту дискретизации в M раз, а затем с помощью децимации уменьшить её в N раз. Фильтрацию сигнала достаточно произвести всего один раз — между интерполяцией и децимацией.Недостатком данного метода является необходимость фильтрации сигнала на повышенной в M раз частоте дискретизации, что требует значительных вычислительных ресурсов. При этом соответствующая частота может во много раз превосходить как исходную, так и окончательную частоту передискретизации, особенно если M и N — близкие большие числа. Так, например, при передискретизации звукового сигнала с 44100 Гц до 48000 Гц этим методом необходимо увеличить частоту дискретизации в 160 раз до 7056000 Гц и затем уменьшить её в 147 раз до 48000 Гц. Таким образом, в данном примере вычисления приходится производить на частоте дискретизации более 7 МГц.
Передискретизация с помощью полифазных фильтров
Метод передискретизации с помощью полифазных фильтров аналогичен предыдущему, с тем отличием, что в нём вместо одного фильтра, работающего на высокой частоте дискретизации, используется несколько фильтров, работающих на низкой частоте. При этом удаётся добиться сокращения количества необходимых вычислений, так как для каждого отсчёта необходимо вычислить выход только одного из этих фильтров.
Передискретизация с помощью дискретного преобразования Фурье
Передискретизация с помощью ДПФ используется для повышения частоты дискретизации в целое или дробное число раз. Алгоритм работает только с конечными отрезками сигнала. Пусть N - начальное число отсчётов, M - число отсчётов в передискретизованном сигнале. Алгоритм включает в себя следующие операции:
1. Вычисляется ДПФ исходного сигнала (чаще всего по алгоритму быстрого преобразования Фурье).
2. В середину спектра вставляется необходимое число нулевых компонент:
- 2.1. если N нечётное:
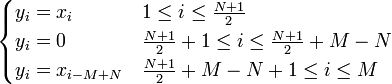
- 2.2. если N чётное
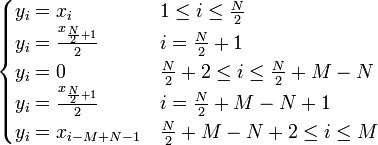
3. Вычисляется обратное ДПФ.
Ограничением этого метода является то, что, как и любой метод, основанный на ДПФ, он даёт точный результат только для периодического дискретного сигнала. Для обработки непериодических сигналов необходимо применять оконные функции и выбирать отрезки сигнала для вычисления ДПФ таким образом, чтобы их концы перекрывались.
Применения
Широко применяется как аппаратная (на основе специализированных микросхем или FPGA), так и программная (на базе процессоров общего назначения или сигнальных процессоров) реализация алгоритмов передискретизации.
Выбор конкретной реализации алгоритма передискретизации является результатом компромисса между качеством преобразования и его вычислительной сложностью. Основным параметром, влияющим на эти характеристики, является близость используемых цифровых фильтров к идеальным. Более качественные фильтры требуют больше ресурсов для вычисления.
На практике передискретизация в большинстве случаев ведёт к потере информации о сигнале по следующим причинам:
- при уменьшении частоты дискретизации сигнал необходимо отфильтровать с целью удаления высокочастотных спектральных составляющих, которые не соответствуют условиям теоремы Котельникова для новой частоты дискретизации;
- вычисления, производимые над цифровыми (квантованными по уровню) сигналами ведут к необратимым ошибкам округления.
Таким образом, при увеличении частоты дискретизации с последующим уменьшением её до исходного значения качество сигнала будет потеряно (если только высокая частота не кратна низкой).
При обработке звука
Оборудование, предназначенное для воспроизведения цифрового звука, как правило, рассчитано на вполне определённую частоту дискретизации сигнала непосредственно перед цифро-аналоговым преобразованием (для многих звуковых карт эта частота составляет 48000 Гц). Все звуковые сигналы с другими частотами дискретизации должны быть рано или поздно передискретизованы.
Передискретизация звукового сигнала на требуемую частоту может осуществляться мультимедиа-проигрывателем, драйвером звуковой карты или самой звуковой картой. Использование программы-проигрывателя для данной цели может быть оправдано, если есть желание избежать аппаратной передискретизации звука (или передискретизации драйвером) с целью добиться более высокого качества (при большей загрузке центрального процессора). Однако программная передискретизация воспроизводимого материала на частоту, отличную от частоты, поддерживаемой оборудованием, не имеет смысла и приводит только к потере качества сигнала.
Существуют программные передискретизаторы звуковых сигналов с открытым исходным кодом:
- SRC (Secret Rabbit Code) или libsamplerate[1] — существует плагин для [2] — существуют плагины для foobar2000.
Также передискретизация поддерживается программами-редакторами звука.
При обработке изображений
Изменение разрешения является одной из распространённых операций обработки изображений. Передискретизация, приближенная к идеальной (с минимизацией наложения спектров), не всегда является желательной. Выбор фильтра для передискретизации является результатом компромисса между типом и выраженностью артефактов и вычислительной сложностью преобразования (актуальной для приложений реального времени).
Типичные артефакты при изменении разрешения изображения:
- Пикселизация (англ. blocking);
- Звон (англ. ringing);
- Алиасинг (англ. aliasing);
- Размытие (англ. blurring).
Для передискретизации изображений применяется большое число фильтров, которые можно классифицировать следующим образом[3]:
- Фильтры интерполяционного типа, обладающие сравнительно узкой импульсной характеристикой. К ним относятся, в частности, треугольный фильтр, производящий билинейную интерполяцию и полином Лагранжа, с помощью которого можно реализовать бикубическую интерполяцию. Применение таких фильтров позволяет осуществить передискретизацию изображения достаточно быстро.
- Фильтры с колоколообразной характеристикой, такие как фильтр Гаусса. Эти фильтры хорошо справляются с пикселизацией, звоном и алиасингом, а также отфильтровывают высокочастотные шумы. Их недостаток — заметное размытие изображения.
- Оконные sinc-фильтры. Sinc-фильтр — это идеальный фильтр нижних частот. Как говорилось выше, он не может быть реализован. Однако если частотную характеристику sinc-фильтра умножить на оконную функцию, получится реализуемый фильтр с хорошими спектральными свойствами. При применении данных фильтров к изображениям удаётся сохранить относительно высокую чёткость (даже при увеличении разрешения), но может быть сильно заметен эффект звона. Одним из наиболее часто применяемых фильтров данного типа является фильтр Ланцоша.
При обработке радиосигналов
При демодуляции цифровых сигналов желательно, чтобы частота дискретизации сигнала была кратна его скорости манипуляции (иначе говоря, чтобы на каждый символ приходилось одинаковое число отсчётов сигнала). Однако частота дискретизации входного сигнала с АЦП, как правило, фиксирована, а скорость манипуляции может меняться. Решением является передискретизация сигнала.
Примечания
- ↑ Secret Rabbit Code (aka libsamplerate)
- ↑ Shibatch Audio Tools
- ↑ Resize and Scaling на сайте программы
Литература
- Richard G. Lyons Understanding digital signal processing. — Addison Wesley, 1997. — 517 с. — ISBN 0-201-63467-8
- Л. Рабинер, Б. Гоулд Теория и применение цифровой обработки сигналов = Theory and Application of Digital Signal Processing. — М.: Мир, 1978. — 848 с.
- Романюк Ю.А. Основы цифровой обработки сигналов. В 3-х ч. Ч.1. Свойства и преобразования дискретных сигналов: Учебное пособие. — М.: МФТИ, 2005. — 332 с. — ISBN 5-74-170144-2
Wikimedia Foundation. 2010.
