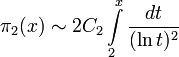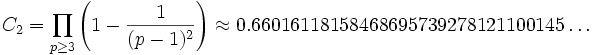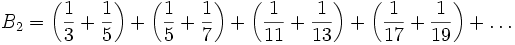- Простые близнецы
-
Простые числа-близнецы это пара простых чисел, отличающихся на 2.
Все пары простых-близнецов, кроме (3, 5) имеют вид
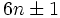 .
.Первые простые числа-близнецы:
(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883)
На данный момент, наибольшими известными простыми-близнецами являются числа
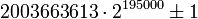 [1].
[1].Предполагается, что таких пар бесконечно много, но это не доказано. По гипотезе Харди-Литтлвуда, количество π2(x) пар простых-близнецов, не превосходящих x, асимптотически приближается к
где C2 — константа простых-близнецов:
Содержание
Теорема Бруна
Вигго Брун в 1919 доказал, что
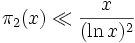 и ряд обратных величин сходится
и ряд обратных величин сходитсяЭто означает, что если простых близнецов и бесконечно много, то они все же расположены в натуральном ряду довольно редко.
Значение
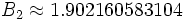 называется константой Бруна для простых-близнецов.
называется константой Бруна для простых-близнецов.Впоследствии была доказана сходимость аналогичного ряда для обобщенных простых близнецов.
Списки
Самые большие известные простые близнецы
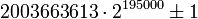 (58711 цифр)
(58711 цифр)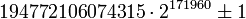 (51780 цифр)
(51780 цифр)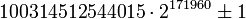 (51780 цифр)
(51780 цифр)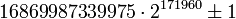 (51779 цифр)
(51779 цифр)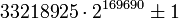 (51090 цифр)
(51090 цифр)
Простые числа-триплеты
Это, тройка различных простых чисел, разность между наибольшим и наименьшим из которых минимальна. Наименьшими, простыми числами, отвечающими заданному условию, являются - (2, 3, 5) и (3, 5, 7). Данная пара триплетов исключительна, так как, во всех остальных случаях, разность между первым и третьим членом равна шести. Обобщёно, последовательность простых чисел (p, p+2, p+6) или (p, p+4, p+6) называется триплетом.
Первые простые числа-триплеты:
(5, 7, 11), (7, 11, 13), (11, 13, 17), (13, 17, 19), (17, 19, 23), (37, 41, 43), (41 , 43, 47), (67, 71, 73), (97, 101, 103), (101, 103, 107), (103, 107, 109), (107, 109, 113), (191, 193 , 197), (193, 197, 199), (223, 227, 229), (227, 229, 233), (277, 281, 283), (307, 311, 313), (311, 313, 317 ), (347, 349, 353), (457, 461, 463), (461, 463, 467), (613, 617, 619), (641, 643, 647), (821, 823, 827), (823, 827, 829), (853, 857, 859), (857, 859, 863), (877, 881, 883), (881, 883, 887)
На данный момент, наибольшими известными простыми-триплетами являются числа:
(p, p+2, p+6), где p = 2072644824759 × 233333 − 1 (10047 цифр, ноябрь, 2008, Norman Luhn, François Morain, FastECPP)
См. также
- Простые Софи Жермен
- Последовательности A001359 и A006512 из Энциклопедии числовых последовательностей.
Wikimedia Foundation. 2010.