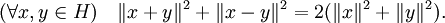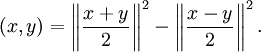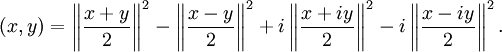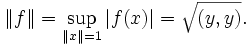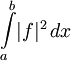Пространство Гильберта

Ги́льбертово простра́нство — особый тип банаховых пространств, обобщение евклидова пространства на бесконечномерный случай. При этом гильбертово пространство не обязательно является бесконечномерным.

Гильбертово пространство есть банахово пространство, норма которого порождена положительно определённым скалярным произведением.

Названо в честь Давида Гильберта.

Связанные определения

• Наименьшая из мощностей подмножеств гильбертова пространства H, для которых замыкание линейной оболочки совпадает с H, называется размерностью пространства H.

Свойства

• Характеристическим свойством, выделяющим гильбертовы пространства H среди прочих банаховых пространств, является тождество параллелограмма:

  $(\forall x,y\in H)\quad \|x+y\|^2+\|x-y\|^2=2(\|x\|^2+\|y\|^2).$

  • Если удовлетворяющее тождеству параллелограмма банахово пространство является вещественным, то отвечающее его норме скалярное произведение задаётся равенством

    $(x,y) = \left\|\dfrac{x+y}{2}\right\|^2-\left\|\dfrac{x-y}{2}\right\|^2.$

  • Аналогично, если это пространство является комплексным, то отвечающее его норме скалярное произведение задаётся равенством

    $(x,y) = \left\|\dfrac{x+y}{2}\right\|^2-\left\|\dfrac{x-y}{2}\right\|^2+ i\left\|\dfrac{x+iy}{2}\right\|^2-i\left\|\dfrac{x-iy}{2}\right\|^2.$

• Любые два гильбертовы пространства, имеющие одинаковую размерность, изоморфны. В частности,
  • любые два бесконечномерные сепарабельные гильбертовы пространства изоморфны друг другу и пространству 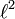$\ell^2$ (см. ниже).
• Теорема Рисса — Фреше: Для любого непрерывного линейного функционала f на Гильбертовом пространстве H существует единственный вектор 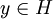$y \in H$ такой, что f(x) = (x,y) для любого 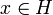$x \in H$. При этом норма линейного функционала f совпадает с нормой вектора y:

  $\|f\|=\sup_{\|x\|=1} |f(x)|= \sqrt{(y,y)}.$

Примеры

• Евклидово пространство.
• Пространство 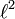$\ell^2$. Его точки суть бесконечные последовательности вещественных чисел 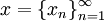$x = \{x_n\}_{n=1}^{\infty}$, для которых сходится ряд 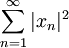$\sum_{n=1}^\infty |x_n|^2$. Скалярное произведение на этом пространстве задаётся равенством

  $(x, y) = \sum_{n=1}^\infty x_n y_n$.

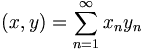• Пространство L²[a,b] измеримых функций с вещественными значениями на отрезке [a,b] с интегрируемыми по Лебегу квадратами — т. е. таких, что интеграл

  $\int\limits_a^b\!|f|^2\,dx$

определён и конечен. Скалярное произведение на этом пространстве задаётся равенством

$(f, g) = \int\limits_a^b\!f{g}\,dx$.

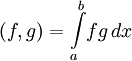Для пространств 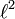$\ell^2$ и L²[a,b] над полем комплексных чисел, последовательностей комплексных чисел и комплекснозначных функций, определение скалярного произведения отличается лишь комплексной сопряжённостью второго сомножителя:

$(x, y) = \sum_{n=1}^\infty x_n \overline{y}_n$;

$(f, g) = \int\limits_a^b\!f\overline{g}\,dx$.

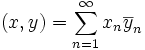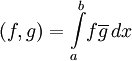См. также

• равенство Парсеваля
• Предгильбертово пространство

Литература

• Халмош П., Гильбертово пространство в задачах, Перевод с английского И. Д. Новикова и Т. В. Соколовской; под ред. Р. А. Минлоса. — М.: Издательство «Мир», 1970. — 352 с.
• Морен К., Методы гильбертова пространства. — М.: Мир, 1965. — 570 c.

Ссылки