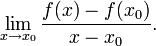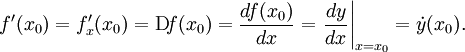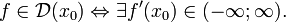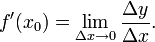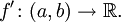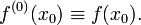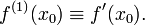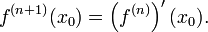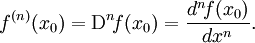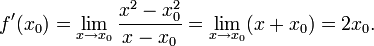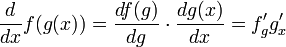Производная функция

Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференци́рованием.

Определение

Пусть в некоторой окрестности точки 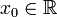$x_0 \in \R$ определена функция 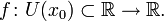$f\colon U(x_0) \subset \R \to \R.$ Производной функции f в точке x₀ называется предел, если он существует,

$\lim\limits_{x \to x_0} \frac{f(x) - f(x_0)}{x - x_0}.$

Общепринятые обозначения производной функции y = f(x) в точке x₀:

$f'(x_0) = f'_x(x_0)=\mathrm{D}\!f(x_0) = \frac{df(x_0)}{dx} = \left.\frac{dy}{dx}\right\vert_{x = x_0} = \dot{y}(x_0).$

Заметим, что последнее обычно обозначает производную по времени (в теоретической механике).

Дифференцируемость

Основная статья: Дифференцируемая функция

Производная f'(x₀) функции f в точке x₀, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x₀ тогда и только тогда, когда её производная в этой точке существует и конечна:

$f \in \mathcal{D}(x_0)\Leftrightarrow\exists f'(x_0) \in (-\infty;\infty).$

Для дифференцируемой в x₀ функции f в окрестности U(x₀) справедливо представление

f(x) = f(x₀) + f'(x₀)(x − x₀) + o(x − x₀) при $x \to x_0.$

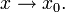
Замечания

• Назовём Δx = x − x₀ приращением аргумента функции, а Δy = f(x₀ + Δx) − f(x₀) приращением значения функции в точке x₀. Тогда

  $f'(x_0) = \lim\limits_{\Delta x \to 0} \frac{\Delta y}{\Delta x}.$

• Пусть функция 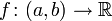$f\colon(a,b) \to \R$ имеет конечную производную в каждой точке 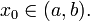$x_0 \in (a,b).$ Тогда определена произво́дная фу́нкция

  $f'\colon(a,b) \to \R.$

• Функция, имеющая конечную производную в точке, непрерывна в ней. Обратное не всегда верно.
• Если производная функция сама является непрерывной, то функцию f называют непреры́вно дифференци́руемой и пишут: $f \in C^{(1)}\bigl((a,b)\bigr).$

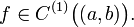
Геометрический и физический смысл производной

Тангенс угла наклона касательной прямой

Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точки x₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло серая линия C). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C₀ — C₅). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Основная статья: Касательная прямая

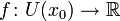Если функция $f\colon U(x_0) \to \R$ имеет конечную производную в точке x₀, то в окрестности U(x₀) её можно приблизить линейной функцией

f_l(x) = f(x₀) + f'(x₀)(x − x₀).

Функция f_l называется касательной к f в точке x₀. Число f'(x₀) является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Скорость изменения функции

Пусть s = s(t) — закон прямолинейного движения. Тогда v(t₀) = s'(t₀) выражает мгновенную скорость движения в момент времени t₀. Вторая производная a(t₀) = s''(t₀) выражает мгновенное ускорение в момент времени t₀.

Вообще производная функции y = f(x) в точке x₀ выражает скорость изменения функции в точке x₀, то есть скорость протекания процесса, описанного зависимостью y = f(x).

Производные высших порядков

Понятие производной произвольного порядка задаётся рекуррентно. Полагаем

$f^{(0)}(x_0) \equiv f(x_0).$

Если функция f дифференцируема в x₀, то производная первого порядка определяется соотношением

$f^{(1)}(x_0) \equiv f'(x_0).$

Пусть теперь производная n-го порядка f⁽ⁿ⁾ определена в некоторой окрестности точки x₀ и дифференцируема. Тогда

$f^{(n+1)}(x_0) = \left(f^{(n)}\right)'(x_0).$

Производные высших порядков обозначаются символами:

$f^{(n)}(x_0) = \mathrm{D}^n\!f(x_0) = \frac{d^n\!f(x_0)}{dx^n}.$

Когда n мало, используются штрихи, римские цифры или точки:

$f^{(1)}(x_0) = f'(x_0) = f^I(x) = \dot{f}(x_0),$

$f^{(2)}(x_0) = f''(x_0) = f^{II}(x) = \ddot{f}(x_0),$

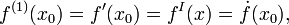
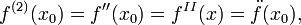
f⁽³⁾(x₀) = f'''(x₀) = f^III(x), и т. д.

Примеры

• Пусть f(x) = x². Тогда

$f'(x_0) = \lim\limits_{x \to x_0}\frac{x^2 - x_0^2}{x-x_0} = \lim\limits_{x \to x_0}(x+x_0) = 2x_0.$

• Пусть f(x) = | x | . Тогда если 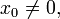$x_0 \neq 0,$ то

f'(x₀) = sgnx₀,

где sgn обозначает функцию знака. Если x₀ = 0, то 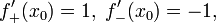$f'_+(x_0) = 1,\; f'_-(x_0) = -1,$ а следовательно f'(x₀) не существует.

Правила дифференцирования

Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.

• (f + g)' = f' + g' (производная суммы равна сумме производных)
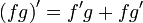• $\left(fg\right)'=f'g+fg'$ (отсюда, в частности, следует, что производная произведения функции и константы равна произведению производной этой функции на константу)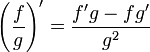
• $\left(\frac{f}{g}\right)'=\frac{f' g-fg'}{g^2}$
• Если функция задана параметрически:

$\left\{\begin{matrix}x=x(t),\\y=y(t),\end{matrix}\; \; t\in\left[T_1; T_2 \right] \right.$, то $y'_x=\frac{d_y}{d_x}=\frac{d_y}{d_t}\cdot \frac{d_t}{d_x}=y'_t\cdot t'_x=\frac{y'_t}{x'_t}$

• $\frac{d}{dx}f(g(x))=\frac{df(g)}{dg}\cdot \frac{dg(x)}{dx}=f'_g g'_x$

Основная статья: Дифференцирование сложной функции

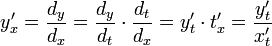
Следующие свойства производной служат дополнением к правилам дифференцирования:

• если функция дифференцируема на интервале (a,b), то она непрерывна на интервале (a,b);
• если функция имеет локальный максимум/минимум при значении аргумента, равном x, то f'(x) = 0 (это так называемая лемма Ферма);
• производная данной функции единственна, но у разных функций могут быть одинаковые производные.

Производная вектор-функции по параметру

Определим производную вектор-функции 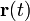$\mathbf{r}(t)$ по параметру:

$\frac{d}{dt}\mathbf{r}(t)=\lim_{h\to 0}\frac{\mathbf{r}(t+h) - \mathbf{r}(t)}{h}$.

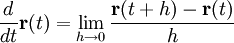Если производная в точке 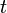$~t$ существует, вектор-функция называется дифференцируемой в этой точке. Координатными функциями для производной будут $x'(t),\ y'(t),\ z'(t)$.

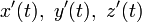Свойства производной вектор-функции (всюду предполагается, что производные существуют):

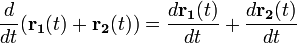• $\frac{d}{dt} (\mathbf{r_1}(t)+\mathbf{r_2}(t))=\frac{d\mathbf{r_1}(t)}{dt}+\frac{d\mathbf{r_2}(t)}{dt}$ — производная суммы есть сумма производных.

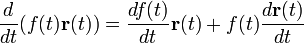• $\frac{d}{dt} (f(t)\mathbf{r}(t))=\frac{df(t)}{dt}\mathbf{r}(t) + f(t)\frac{d\mathbf{r}(t)}{dt}$ — здесь 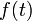$~f(t)$ — дифференцируемая скалярная функция.

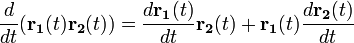• $\frac{d}{dt} (\mathbf{r_1}(t)\mathbf{r_2}(t))=\frac{d\mathbf{r_1}(t)}{dt}\mathbf{r_2}(t) + \mathbf{r_1}(t)\frac{d\mathbf{r_2}(t)}{dt}$ — дифференцирование скалярного произведения.

• $\frac{d}{dt} [\mathbf{r_1}(t)\mathbf{r_2}(t)]=\left [\frac{d\mathbf{r_1}(t)}{dt}\mathbf{r_2}(t)\right ] + \left [\mathbf{r_1}(t) \frac{d\mathbf{r_2}(t)}{dt}\right]$ — дифференцирование векторного произведения.

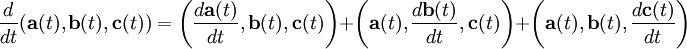• $\frac{d}{dt} (\mathbf{a}(t),\mathbf{b}(t),\mathbf{c}(t))=\left (\frac{d\mathbf{a}(t)}{dt},\mathbf{b}(t),\mathbf{c}(t)\right) + \left (\mathbf{a}(t),\frac{d\mathbf{b}(t)}{dt},\mathbf{c}(t)\right) + \left (\mathbf{a}(t), \mathbf{b}(t), \frac{d\mathbf{c}(t)}{dt}\right)$ — дифференцирование смешанного произведения.

См. также

• Таблица производных
• Дифференцирование сложной функции
• Первообразная
• Обобщения производных
• Основная теорема анализа
• Геометрический смысл производной
• Экономический смысл производной
• Частная производная
• Производная по направлению

Литература

• В. Г. Болтянский, Что такое дифференцирование?, «Популярные лекции по математике», Выпуск 17, Гостехиздат 1955 г., 64 стр.
• В. А. Гусев, А. Г. Мордкович «Математика»

Ссылки

Онлайн Калькулятор Производных