- Преобразование плоскости
-
Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице).
# А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ы Э Ю Я
N
- n-угольник — многоугольник с n вершинами.
А
- Аффи́нное преобразование — преобразование плоскости, переводящее прямые в прямые.
- Антипаралле́ль к стороне BC — отрезок B1C1, где точки B1 и C1 лежат на лучах AC и AB, при условии, что ∠AB1C1 = ∠ABC и ∠AC1B1 = ∠ACB.
- Асимпто́та кривой γ, имеющей бесконечную ветвь, — прямая, такая, что расстояние от точки γ кривой до этой прямой стремится к нулю при движении ее вдоль ветви к бесконечности.
Б
- Барице́нтр системы точек Ai с массами mi — точка Z такая что
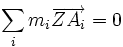 .
.
- Барицентри́ческие координаты точки X относительно невырожденного треугольника ABC — тройка чисел (m1:m2:m3), такая что
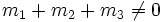 и
и 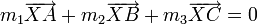 , то есть если разместить в вершины треугольника массы, численно равные m1,m2,m3, то барицентр полученной системы точек совпадёт с точкой X. Барицентрические координаты называют приведёнными, если m1 + m2 + m3 = 1
, то есть если разместить в вершины треугольника массы, численно равные m1,m2,m3, то барицентр полученной системы точек совпадёт с точкой X. Барицентрические координаты называют приведёнными, если m1 + m2 + m3 = 1
- Биссектри́са треугольника, проведенная из вершины — отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противоположной стороне.
- Биссектри́са угла — луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.
В
- Вневпи́санная окружность треугольника. Окружность, касающаяся одной из сторон треугольника и продолжений двух других его сторон.
- Внешний угол — см. многоугольник.
- Внутренний угол — см. многоугольник.
- Впи́санная окружность треугольника. Окружность, касающаяся трёх сторон треугольника.
- Впи́санный четырёхуго́льник. Выпуклый четырёхугольник, все вершины которого лежат на одной окружности.
- Высота треугольника. Высотой треугольника называют перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. Иногда так называют длину этого перпендикуляра.
Г
- Геометрическое место точек (ГМТ) — множество точек плоскости, удовлетворяющее определённому условию. Например, срединный перпендикуляр к отрезку есть геометрическое место точек, равноудалённых от его концов.
- Гипербола
- Гомотетия с центром O и коэффициентом
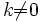 — преобразование плоскости, переводящее точку P в точку P' , такую что
— преобразование плоскости, переводящее точку P в точку P' , такую что 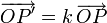 .
.
Д
- Движение. см. изометрия.
- Диаметр Брокара — диаметр окружности Брокара.
И
- Изоме́трия. Преобразование, сохраняющее расстояния.
- Инве́рсия — конформное преобразование, при котором окружности и прямые переходят в прямые и окружности (не обязательно соответственно).
- Инце́нтр треугольника — точка пересечения биссектрис, а также центр вписанной в треугольник окружности.
- Изогональное сопряжение. Пусть на сторонах BC, CA и AB треугольника ABC взяты точки A1, B1 и C1, причем прямые AA1, BB1 и CC1 пересекаются в одной точке P. Тогда прямые AA2, BB2 и CC2, симметричные этим прямым относительно соответствующих биссектрис, также пересекаются в одной точке Q. В этом случае точки P и Q называются изогонально сопряженными относительно треугольника ABC.
- Изогонический центр треугольника. Построим на сторонах треугольника ABC внешним (внутренним) образом правильные треугольники ABC1, AB1C и A1BC. Тогда прямые AA1, BB1 и CC1 пересекаются в одной точке. Эту точку называют первым (вторым) изогоническим центром. Первый изогонический центр называют также точкой Ферма.
- Изодинамический центр треугольника. Пусть AD и AE — биссектрисы внутреннего и внешнего углов треугольника ABC и Sa — окружность с диаметром DE, окружности Sb и Sc определяются аналогично. Тогда эти три окружности имеют две общие точки M и N, которые называются изодинамическими центрами. Кроме того, прямая MN проходит через центр описанной окружности треугольника ABC.
К
- Коллинеа́рные точки. Набор точек, находящихся на одной прямой.
- Конгруэ́нтные фигуры. Две фигуры называются конгруэнтными, если существует изометрия плоскости, которая переводит одну в другую.
- Конкуре́нтные прямые. Набор прямых, проходящих через одну точку, или попарно параллельных.
- Кривая постоянной ширины a есть замкнутая выпуклая кривая, длина проекции которой на любую прямую равна a.
- Круг есть ограниченная часть плоскости, ограниченная окружностью.
- Круговая плоскость. Евклидова плоскость, дополненная одной идеальной точкой (
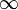 ).
).
Л
- Луч — «полупрямая», имеет начальную точку, но не имеет конечной точки.
М
- Медиа́на треугольника. Отрезок соединяющий вершину треугольника с серединой противоположной стороны.
- Многоуго́льник. Замкнутая ломаная на плоскости.
Н
- Накло́нная к прямой p ― прямая, пересекающая прямую p под углом, отличным от прямого.
О
- Окру́жность с центром в точке О — геометрическое место точек, равноудалённых от точки О.
- Окру́жность Аполло́ния для данных точек A и B и коэффициента
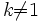 — геометрическое место точек, таких, что | AX | = k | BX | .
— геометрическое место точек, таких, что | AX | = k | BX | .
- Окружность Брокара — описанная окружность треугольника Брокара.
- Окружности Лемуана. Через точку Лемуана данного треугольника проведем прямые, параллельные сторонам этого треугольника. Окружность, проходящая через точки их пересечения со сторонами треугольника (в общем случае таких точек 6), называется первой окружностью Лемуана. Если же через точку Лемуана провести прямые, антипараллельные сторонам треугольника, то окружность, проходящая через точки их пересечения со сторонами треугольника называется второй окружностью Лемуана.
- Окружность Нейберга Пусть вершины B и C треугольника фиксированы, а вершина A движется так, что угол Брокара
 треугольника ABC остается постоянным. Тогда точка A движется по окружности радиуса
треугольника ABC остается постоянным. Тогда точка A движется по окружности радиуса 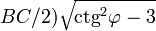 , которая и называется окружностью Нейберга.
, которая и называется окружностью Нейберга.
- Окружность Тукера треугольника ABC — окружность, которая проходит через точки пересечения сторон треугольника ABC с продолжениями сторон треугольника A1B1C1, полученного из треугольника ABC при гомотетии с центром в точке Лемуана. Эти точки (в общем случае их шесть) всегда лежат на одной окружности. Центр окружности Тукера лежит между точкой Лемуана и центром описанной окружности.
- Окружности Схоуте. Опустим из точки M перпендикуляры MA1, MB1 и MC1 на прямые BC, CA и AB. Для фиксированного треугольника ABC множество точек M, для которых угол Брокара треугольника A1B1C1 имеет заданное значение, состоит из двух окружностей, причем одна из них расположена внутри описанной окружности треугольника ABC, а другая вне ее. Данные окружности называются окружностями Схоуте треугольника ABC. 'Отре́зок — часть прямой между двумя точками, включая концы.
- Описанная окружность многоугольника — окружность, содержащая все вершины многоугольника. Многоугольник, вокруг которого описанна окружность, называется вписанным в эту окружность.
П
- Параллелогра́мм — четырехугольник, противоположные стороны и противоложные углы которого равны.
- Параллельный перенос — преобразование M'=f(M) такое, что все отрезки MM' равны и параллельны. Из этого вытекает, что x' = x + a1, y' = y + a2, где a1,a2 — произвольные константы. Параллельный перенос является изометрией и не имеет неподвижных точек.
- Педа́льный треугольник см. Подерный треугольник
- Площадь — некоторая аддитивная неотрицательная величина, сопоставляемая каждой элементарной фигуре.
- Поворот — изометрическое преобразование, являющееся результатом вращения всей плоскости вокруг точки на этой плоскости на заданный угол.
- Поде́рный треугольник точки Р относительно ∆ABC. Треугольник, вершинами которого являются основания перпендикуляров, опущенных из точки Р на стороны треугольника ABC (или их продолжения).
- Подобие — преобразование, сохраняющее отношение расстояний.
- Преобразование плоскости — взаимнооднозначное отображение плоскости на себя. Часто однако преобразванием называют отображения, которые продолжаются до преобразований расширенной плоскости, например инверсия — преобразование круговой плоскости, перспектива — преобразование проективной плоскости, и т. д.
- Проективная плоскость — евклидова плоскость, дополненная идеальной прямой (см. бесконечно удалённая прямая).
- Проективные преобразования — преобразования проективной плоскости, сохраняющие отношение параллельности.
- Прямая Эйлера
Р
- Равновеликие фигуры — фигуры имеющие одинаковую площадь.
- Ромб — параллелограмм, у которого все стороны равны. Частным случаем ромба является квадрат.
С
- Симедиана — отрезок, симметричный медиане треугольника относительно биссектрисы угла этого треугольника. Симедианы треугольника пересекаются в точке Лемуана.
- Серединный перпендикуляр к отрезку — прямая, перпендикулярная к отрезку и делящая его на две равные части.
- Серединный треугольник — треугольник, образованный средними линиями исходного треугольника.
- Средняя линия треугольника или трапеции — отрезок, соединяющий середины боковых сторон. Средняя линия параллельна основанию треугольника (или основаниям трапеции) и равна половине основания треугольника (или полусумме оснований трапеции).
- Степень точки относительно окружности — число d2 − R2, где d — расстояние от точки до центра окружности, a R — радиус окружности.
- Стереографическая проекция — проекция из точки О сферы, проходящей через эту точку на плоскость, касающуюся сферы в точке, антиподальной к точке О.
- Скользящая симметрия — композиция симметрии относительно некоторой прямой и переноса на вектор, параллельный этой прямой (этот вектор может быть и нулевым).
Т
- Точка Жерго́на — точка пересечения чевиан, проходящих через точки касания вписанной окружности со сторонами этого треугольника.
- Точка Лемуана — точка пересечения симедиан треугольника. Эта точка изогонально сопряженна центроиду.
- Точка На́геля — точка пересечения прямых, соединяющих вершины треугольника с точками касания противоположных сторон с вневписанными окружностями.
- Точка Торричелли — точка, из которой все стороны видны под углом 120°.
- Точки Брокара — такие внутренние точки P и Q
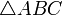 , что
, что 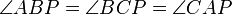 и
и 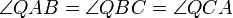 .
.
- Треугольник Наполеона для треугольника — равносторонний треугольник, образованный центрами равносторонних треугольников, построенных на всех сторонах данного треугольника.
- Трисектри́са угла есть луч, делящий этот угол в отношении 2:1.
- Трисектри́са — плоская кривая.
- Тупой угол — угол, величина которого находится между 90 и 180 градусами.
- Теорема Гаусса. Рассмотрим четырехугольник ABCD. Пусть u = AD2, v = BD2, w = CD2, U = BD2 + CD2 - BC2, V = AD2 + CD2 - AC2, W = AD2 + BD2 - AB2. Тогда uU2 + vV2 + wW2 = UVW + 4uvw.
- Теорема Карно. Перпендикуляры, опущенные из точек A1, B1 и C1 на стороны BC, CA и AB треугольника ABC, пересекаются в одной точке тогда и только тогда, когда A1B2 + C1A2 + B1C2 = B1A2 + A1C2 + C1B2.
- Теорема Наполеона. Если на сторонах правильного треугольника внешним (внутренним) образом построены правильные треугольники, то их центры образуют правильный треугольник. Кроме того, разность площадей треугольников, полученных при построении правильных треугольников внешним и внутренним образом, равна площади исходного треугольника.
- Теорема о группировке масс. Центр масс системы точек останется прежним, если часть точек заменить одной точкой, которая расположена в их центре масс и которой приписана масса, равная сумме масс удаленных точек.
- Теорема о дважды перспективных треугольниках. Рассмотрим два треугольника ABC и A1B1C1 таких, что прямые AA1, BB1 и CC1 пересекаются в одной точке O, и прямые AB1, BC1 и CA1 пересекаются в одной точке O1. Тогда прямые AC1, BA1 и CB1 тоже пересекаются в одной точке O2.
- Теорема о полном четырехстороннике. Рассмотрим четыре точки A, B, C и D. Пусть P, Q и R — точки пересечения прямых AB и CD, AD и BC, AC и BD соответственно; K и L — точки пересечения прямой QR с прямыми AB и CD соответственно. Тогда (QRKL)=-1, где (QRKL) — двойное отношение точек Q, R, K, L</math>.
- Теорема о трижды перспективных треугольниках. Рассмотрим два треугольника ABC и A1B1C1 таких, что прямые AA1, BB1 и CC1 пересекаются в одной точке O, прямые AA1, BC1 и CB1 пересекаются в одной точке O1 и прямые AC1, BB1 и CA1 пересекаются в одной точке O2. Тогда прямые AB1, BA1 и CC1 также пересекаются в одной точке O3.
- Теорема Тебо: На стороне BC треугольника ABC взята точка D. Окружность S1 касается отрезков BE и EA и описанной окружности, окружность S2 касается отрезков CE и EA и описанной окружности. Пусть I, I1, I2 и r, r1, r2 — центры и радиусы вписанной окружности и окружностей S1, S2;
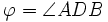 . Тогда точка I лежит на отрезке I1I2, причём
. Тогда точка I лежит на отрезке I1I2, причём 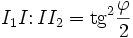 , причем
, причем 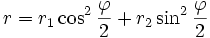 (Тебо).
(Тебо).
- Теорема Шаля утверждает, что любое движение плоскости является одним из следующего списка: параллельный перенос, поворот, скользящая симметрия (включая осевую). Теорема Шаля дает полную классификацию всех движений плоскости.
- — Часто также бывает удобно воспользоваться тем фактом, что любое движение плоскости есть композиция некоторого количества осевых симметрий (всегда можно обойтись не более, чем тремя).
- — Аналогичная теорема классифицирует все движения трехмерного пространства: всякое сохраняющее ориентацию движение пространства является винтовым движением (то есть композицией поворота вокруг определенной оси с параллельным переносом вдоль той же оси, причем как угол, так и вектор могут быть и нулевыми). Движение, меняющее ориентацию, является композицией симметрии относительно плоскости и винтового движения.
- Точки изотомически сопряженные Пусть прямые AP,BP и CP пересекают прямые BC,CA и AB в точках A1,B1 и C1 соответственно, а точки A2,B2 и C2 выбраны на прямых BC,CA и AB так, что
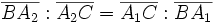 ,
, 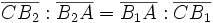 и
и 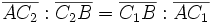 . Тогда прямые AA2,BB2 и CC2 либо параллельны, либо также пересекаются в одной точке Q. В последнем случае точки P и Q называют изотомически сопряженными относительно треугольника ABC.
. Тогда прямые AA2,BB2 и CC2 либо параллельны, либо также пересекаются в одной точке Q. В последнем случае точки P и Q называют изотомически сопряженными относительно треугольника ABC.
- Точки постоянные подобных фигур Пусть l1, l2 и l3 — соответственные прямые подобных фигур F1, F2 и F3, пересекающиеся в точке W. Пусть J1, J2 и J3 — точки пересечения прямых l1, l2 и l3 с окружностью подобия, отличные от точки W. Оказывается, что эти точки зависят только от фигур F1, F2 и F3 и не зависят от выбора прямых l1, l2 и l3. Точки J1, J2 и J3 и называют постоянными точками подобных фигур F1, F2 и F3, а треугольник J1J2J3 называют постоянным треугольником подобных фигур F1, F2 и F3.
- Точки соответственные Точки A1 и A2 называют соответственными точками подобных фигур F1 и F2, если при поворотной гомотетии, переводящей F1 в F2, точка A1 переходит в A2. Аналогично определяются соответственные прямые и отрезки.
- Треугольник Брокара — треугольник с вершинами в постоянных точках треугольника.
- Треугольник подобия Пусть F1, F2 и F3 — три подобные фигуры, O1 — центр поворотной гомотетии, переводящей F2 в F3, точки O2 и O3 определяются аналогично. Если точки O1, O2 и O3 не лежат на одной прямой, то треугольник O1O2O3 называют треугольником подобия фигур F1, F2 и F3, а его описанную окружность называют окружностью подобия этих фигур. В случае, когда точки O1, O2 и O3 совпадают, окружность подобия вырождается в центр подобия, а в случае, когда эти точки не совпадают, но лежат на одной прямой, окружность подобия вырождается в ось подобия
- Треугольник постоянный См. точки постоянные подобных фигур.
- Треугольники ортологические — треугольники ABC и A1B1C1, для которых перпендикуляры, опущенные из точек A, B и C на прямые B1C1, C1A1 и A1B1 пересекаются в одной точке. В этом случае и перпендикуляры, опущенные из точек A1, B1 и C1 на прямые BC, CA и AB также пересекаются в одной точке.
У
- Угол Брокара. Пусть P — точка Брокара треугольника ABC. Угол
 = ∠ABP = ∠BCP = ∠CAP называется углом Брокара этого треугольника.
= ∠ABP = ∠BCP = ∠CAP называется углом Брокара этого треугольника.
- Угол между окружностями — угол между касательными к окружностям в точке пересечения этих окружностей. Оба угла между двумя пересекающимися окружностями равны.
- Угол между окружностью и прямой — угол между прямой и касательной к окружности в точке пересечения прямой и окружности. Оба угла между пересекающимися окружностью и прямой равны.
Ф
- Фигура — произвольное подмножество плоскости.
Х
- Хо́рда кривой — отрезок, концы которого лежат на данной кривой.
Ц
- Центр масс см. Барицентр.
- Центральная симме́три́я Центра́льной симме́три́ей относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через ZA, в то время как обозначение SA можно перепутать с осевой симметрией. Это преобразование эквивалентно повороту на 180° относительно точки А.
- Центро́ид треугольника. Точка пересечения медиан треугольника.
Ч
- Чевиа́на — отрезок (или продолжение отрезка), соединяющий вершину треугольника с точкой на противоположной ей стороне или на её продолжении.
Ссылки
Wikimedia Foundation. 2010.
