- Преобразование Кармана — Трефтца
-
Функцией Жуковского называется функция вида
 .
.Она относится к классическим элементарным функциям комплексного анализа, так как большинство тригонометрических и гиперболических функций представимы в виде суперпозиции экспоненты и функции Жуковского.
Применение её в аэродинамике основано на том факте, что функция Жуковского отображает окружность на некую замкнутую кривую, подобную профилю самолетного крыла в разрезе. Вариацией радиуса и положения круга относительно 0 можно менять угол изгиба и толщину крыла.
Расчёт потенциального потока для окружности (в двумерном случае) выполняется достаточно просто. Далее можно применить к результату преобразование Жуковского и получить потенциальный поток для профиля крыла, соответствующего данной окружности. И на основании его делать выводы о подьёмной силе, сопротивлении...
Преобразование Кармана — Трефтца
Для более тонкого построения применяется представление функции Жуковского в виде суперпозиции трех функций, в каждой из которых может присутствовать некий параметр. Вкупе с вариацией отображаемого круга так называемая обобщенная функция Жуковского или преобразование Кармана — Трефтца представляет собой мощный инструмент для моделирования:
 , где
, где ,
, ,
,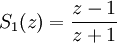 .
.
Wikimedia Foundation. 2010.
