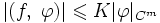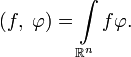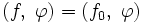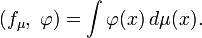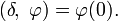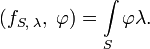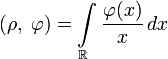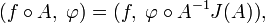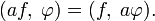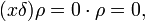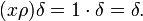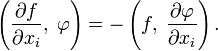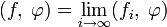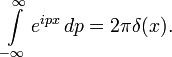Основная функция

Обобщённая фу́нкция или распределе́ние — математическое понятие, обобщающее классическое понятие функции. Потребность в таком обобщении возникает во многих физических и математических задачах.

Понятие обобщённой функции даёт возможность выразить в математически корректной форме такие идеализированные понятия, как плотность материальной точки, точечного заряда, точечного диполя, (пространственную) плотность простого или двойного слоя, интенсивность мгновенного источника и т. д.

С другой стороны, в понятии обобщённой функции находит отражение тот факт, что реально нельзя измерить значение физической величины в точке, а можно измерять лишь её средние значения в малых окрестностях данной точки. Таким образом, техника обобщённых функций служит удобным и адекватным аппаратом для описания распределений различных физических величин.

Обобщённые функции были введены впервые в конце 20-х годов XX в. Дираком в его исследованиях по квантовой механике, где он систематически использует понятие δ-функции и её производных.

Основы математической теории обобщённых функций были заложены Соболевым при решении задачи Коши для гиперболических уравнений, а в 50-х годах Шварц дал систематическое изложение теории обобщённых функций и указал многие применения.

В дальнейшем теория обобщённых функций интенсивно развивалась многими математиками и физиками-теоретиками, главным образом в связи с потребностями теоретической и математической физики и теории дифференциальных уравнений ^[1].

Определение

Формально обобщённая функция f определяется как линейный непрерывный функционал над тем или иным векторным пространством достаточно «хороших функций» (так называемых основных функций) 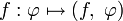$f:\varphi\mapsto(f,\;\varphi)$. 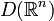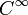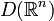Важным примером основного пространства является пространство $D(\R^n)$ — совокупность финитных $C^\infty$-функций на $\R^n$, снабжённая естественной для неё топологией: последовательность функций из $D(\R^n)$ сходится, если их носители принадлежат фиксированному шару и в нём они 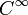$C^\infty$-сходятся.

Сопряжённое пространство к 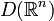$D(\R^n)$ есть пространство обобщённых функций $D'(\R^n)$.

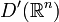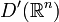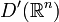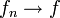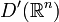Сходимость последовательности обобщённых функций из $D' (\R^n)$ определяется как слабая сходимость функционалов из $D'(\R^n)$, то есть $f_n\to f$, в $D'(\R^n)$ означает, что 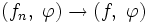$(f_n,\;\varphi)\to(f,\;\varphi)$, для любой $\varphi\in D(\R^n)$.

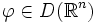Для того, чтобы линейный функционал f на 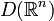$D(\R^n)$ был обобщённой функцией, то есть 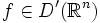$f\in D'(\R^n)$, необходимо и достаточно, чтобы для любого ограниченного открытого множества Ω существовали числа K и m такие, что

$|(f,\;\varphi)|\leqslant K|\varphi|_{C^m}$

для всех $\varphi$ с носителем в Ω.

Если в неравенстве число m можно выбрать не зависящим от Ω, то обобщённая функция f имеет конечный порядок; наименьшее такое m называется порядком f.

Простейшими примерами обобщённых функций являются функционалы, порождаемые локально суммируемыми функциями

$(f,\;\varphi)=\int\limits_{\R^n}f\varphi.$

Обобщённые функции, определяемые локально суммируемыми в функциями f(x) по этой формуле, называются регулярными; остальные обобщённые функции называются сингулярными.

Обобщённые функции вообще говоря, не имеют значений в отдельных точках. Тем не менее можно говорить о совпадении обобщённой функции с локально суммируемой функцией на открытом множестве: обобщённая функция f из 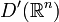$D'(\R^n)$ совпадает в Ω с локально суммируемой в Ω функцией f₀(x), если

$(f,\;\varphi)=(f_0,\;\varphi)$

для всех $\varphi$ с носителм в Ω. В частности, при f₀ = 0 получается определение того, что обобщённая функция f обращается в нуль внутри Ω.

Множество точек, ни в какой окрестности которых обобщённая функция не обращается в ноль, называется носителем обобщённой функции f и обозначается 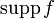$\mathrm{supp}\,f$. Если 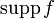$\mathrm{supp}\,f$ компактен, то обобщённая функция f называется финитной.

Примеры

• Любая локально конечная мера μ определяет обобщённую функцию f_μ

$(f_\mu,\;\varphi)=\int\varphi(x)\,d\mu(x).$

В частности,

• Примером сингулярной обобщённой функции в $\R^n$ служит δ-функция Дирака

$(\delta,\;\varphi)=\varphi(0).$

Она описывает плотность массы 1, сосредоточенной в точке x = 0. δ-функция имеет порядок 1.

• Поверхностная δ-функция. Пусть S — кусочно гладкая поверхность и λ — непрерывная функция на S. Обобщённая функция 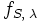$f_{S,\;\lambda}$ определяется равенством

$(f_{S,\;\lambda},\;\varphi)=\int\limits_S\varphi\lambda.$

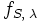При этом $f_{S,\;\lambda}$ — сингулярная обобщённая функция. Эта обобщённая функция описывает пространственную плотность масс пли зарядов, сосредоточенных на поверхности S с поверхностной плотностью λ (плотность простого слоя).

• Обобщённая функция 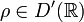$\rho\in D'(\R)$ определяемая равенством

$(\rho,\;\varphi)=\int\limits_\R\frac{\varphi(x)}{x}\,dx$

(для гладких финитных функций этому интегралу можно придать смысл) функция ρ сингулярна и её порядок равен 2, однако на открытом множестве 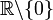$\R\backslash\{0\}$ она регулярна и совпадает с $\frac{1}{x}$.

Операции

Линейные операции над обобщёнными функциями вводятся как расширение соответствующих операций над основными функциями.

Замена переменных

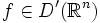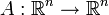Пусть $f\in D'(\R^n)$ и $A:\R^n\to\R^n$ — гладкая замена переменных. Обобщённая функция 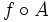$f\circ A$ определяется равенством

$(f\circ A,\;\varphi)=(f,\;\varphi\circ A^{-1}J(A)),$

где J(A) обозначает якобиан A. Эту формулу можно применять в частности к линейному отображению A, она позволяет определить трансляционно инвариантные, сферически симметричные, центрально симметричные, однородные, периодические, лоренц-инвариантные и т. д. обобщённые функции.

Произведение

Чаще всего определяется произведение обобщённых функций на обычные, а произведение обобщённых функций остается неопределенным.

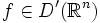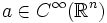Пусть $f\in D'(\R^n)$ и $a\in C^\infty(\R^n)$. Произведение af = fa определяется равенством

$(af,\;\varphi)=(f,\;a\varphi).$

Например aδ = a(0)δ, xρ = 1. Для обычных локально суммируемых функций произведение af совпадает с обычным умножением функций f(x) и a(x).

Однако эта операция произведения вообще говоря не допускает распространения на любые обобщённые функции так, чтобы она была ассоциативной и коммутативной.

Действительно, в противном случае получилось бы противоречие:

$(x\delta)\rho=0\cdot\rho=0,$

$(x\rho)\delta=1\cdot\delta=\delta.$

В частности, Ю. М. Широков построил некоммутативную алгебру обобщённых функций^[2][3].

Дифференцирование

Пусть 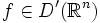$f\in D'(\R^n)$. Обобщённая (слабая) производная обобщённой функции 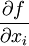$\frac{\partial f}{\partial x_i}$ определяется равенством

$\left(\frac{\partial f}{\partial x_i},\;\varphi\right)=-\left(f,\;\frac{\partial\varphi}{\partial x_i}\right).$

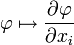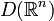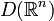Так как операция $\varphi\mapsto\frac{\partial\varphi}{\partial x_i}$ линейна и непрерывна из $D(\R^n)$ в $D(\R^n)$, то функционал, определяемый правой частью равенства, есть обобщённая функция.

Свойства

• Пространство 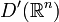$D'(\R^n)$ — полное: если последовательность обобщённых функций f_i из 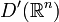$D'(\R^n)$ такова, что для любой функции 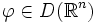$\varphi\in D(\R^n)$ числовая последовательность 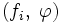$(f_i,\;\varphi)$ сходится, то функционал

$(f,\;\varphi)= \lim_{i\to\infty}(f_i,\;\varphi)$

принадлежит $D'(\R^n)$.

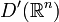• Всякая f из 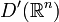$D'(\R^n)$ есть слабый предел функций из 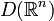$D(\R^n)$. Это свойство иногда берётся в качестве исходного для определения обобщённой функции, из полноты пространства обобщённых функций это приводит к эквивалентному определению.
• Любая обобщённая функция из 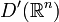$D'(\R^n)$ бесконечно дифференцируема (в обобщённом смысле).
• Дифференцирование не увеличивает носителя обобщённой функции.
• Для обобщённых функций справедлива формула Лейбница для дифференцирования произведения af, где $a\in C^\infty(\R^n)$.
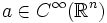• Всякая обобщённая функция f из 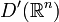$D'(\R^n)$ есть некоторая частная производная от непрерывной функции в $\R^n$.
• Для любой обобщённой функции f порядка N с носителем в точке 0 существует единственное представление 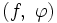$(f,\;\varphi)$ в виде линейной комбинации частных производных $\varphi$ в нуле, с порядком меньшим либо равным N.

Примеры

Дельта-функция получается при вычислении интеграла Фурье от константы:

$\int\limits_{-\infty}^{\infty}e^{ipx}\,dp=2\pi\delta(x).$

Примечания

1. ↑ Обобщенные функции и действия над ними.
2. ↑ Ю. М. Широков, Алгебра одномерных обобщенных функций. — Теоретическая и математическая физика. — 1979. — том 39. — № 3. — стр. 291—301.
3. ↑ Г. К. Толоконников. Об Алгебрах Ю. М. Широкова. — Теоретическая и математическая физика. — 1979. — том 39. — № 3. — стр. 366—375.

См. также

• Спор о струне