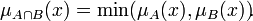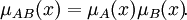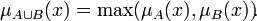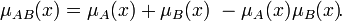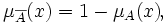- Нечеткое множество
-
Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество — понятие, введённое Лотфи Заде в 1965 г. в статье «Fuzzy Sets» (нечёткие множества) в журнале Information and Control [1]. Л. Заде расширил классическое канторовское понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0,1], а не только значения 0 или 1.
Содержание
Определение
Под нечётким множеством
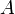 понимается совокупность
понимается совокупность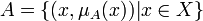 ,
,где
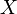 — универсальное множество, а
— универсальное множество, а 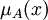 — функция принадлежности (характеристическая функция), характеризующая степень принадлежности элемента
— функция принадлежности (характеристическая функция), характеризующая степень принадлежности элемента 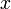 нечёткому множеству
нечёткому множеству 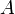 .
.Функция
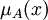 принимает значения в некотором вполне упорядоченном множестве
принимает значения в некотором вполне упорядоченном множестве 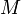 . Множество
. Множество 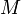 называют множеством принадлежностей, часто в качестве
называют множеством принадлежностей, часто в качестве 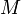 выбирается отрезок
выбирается отрезок ![[0, 1] \](/pictures/wiki/files/98/bc5aec02790c5998360e5dae043f3a51.png) . Если
. Если 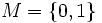 , то нечёткое множество может рассматриваться как обычное, чёткое множество.
, то нечёткое множество может рассматриваться как обычное, чёткое множество.Основные определения
Пусть
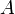 нечёткое множество с элементами из универсального множества
нечёткое множество с элементами из универсального множества 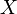 и множеством принадлежностей
и множеством принадлежностей ![M = [0, 1] \](/pictures/wiki/files/52/47064879f7ff287903f285a7efdcc9b6.png) . Тогда
. Тогда- Носителем (суппортом) нечёткого множества
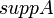 называется множество
называется множество 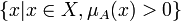 .
. - Величина
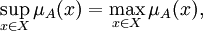
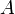 . Нечёткое множество
. Нечёткое множество 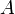 нормально, если его высота равна
нормально, если его высота равна 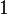 . Если высота строго меньше
. Если высота строго меньше 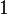 , нечёткое множество называется субнормальным.
, нечёткое множество называется субнормальным. - Нечёткое множество пусто, если
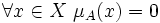 . Непустое субнормальное нечёткое множество можно нормализовать по формуле:
. Непустое субнормальное нечёткое множество можно нормализовать по формуле:
-
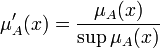
- Нечёткое множество унимодально, если
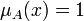 только на одном
только на одном 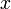 из
из 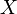 .
. - Элементы
 , для которых
, для которых 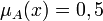 , называются точками перехода нечёткого множества
, называются точками перехода нечёткого множества 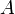 .
.
Сравнение нечётких множеств
Пусть A и B нечёткие множества, заданные на универсальном множестве X.
- A содержится в B, если для любого элемента из X функция его принадлежности множеству A будет принимать значение меньшее либо равное, чем функция принадлежности множеству B:
- В случае, если условие
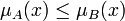 выполняется не для всех
выполняется не для всех  , говорят о степени включения нечёткого множества A в B, которое определяется так:
, говорят о степени включения нечёткого множества A в B, которое определяется так:
где
- Два множества называются равными, если они содержатся друг в друге:
- В случае, если значения функций принадлежности
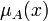 и
и 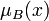 почти равны между собой, говорят о степени равенства нечётких множеств A и B, например, в виде
почти равны между собой, говорят о степени равенства нечётких множеств A и B, например, в виде
где
Свойства нечётких множеств
- α-разрезом нечёткого множества
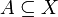 , обозначаемым как
, обозначаемым как 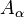 , называется следующее чёткое множество:
, называется следующее чёткое множество:
то есть множество, определяемое следующей характеристической функцией (функцией принадлежности):
Для α-разреза нечёткого множества истинна импликация
- Нечёткое множество
 является выпуклым тогда и только тогда, когда выполняется условие
является выпуклым тогда и только тогда, когда выполняется условие
для любых
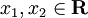 и
и ![\gamma \in [0,1]\!](/pictures/wiki/files/56/83e14ac251be09a30ad4aee2da41420e.png) .
.- Нечёткое множество
 является вогнутым тогда и только тогда, когда выполняется условие
является вогнутым тогда и только тогда, когда выполняется условие
для любых
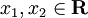 и
и ![\gamma \in [0,1]\!](/pictures/wiki/files/56/83e14ac251be09a30ad4aee2da41420e.png) .
.Операции над нечёткими множествами
При
![M = [0, 1] \](/pictures/wiki/files/52/47064879f7ff287903f285a7efdcc9b6.png)
- Пересечением нечётких множеств A и B называется наибольшее нечёткое подмножество, содержащееся одновременно в A и B:
- Произведением нечётких множеств A и B называется нечёткое подмножество с функцией принадлежности:
- Объединением нечётких множеств A и B называется наименьшее нечёткое подмножество, содержащее одновременно A и B:
- Суммой нечётких множеств A и B называется нечёткое подмножество с функцией принадлежности:
- Отрицанием множества
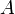 при
при ![M = [0, 1] \](/pictures/wiki/files/52/47064879f7ff287903f285a7efdcc9b6.png) называется множество
называется множество 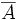 с функцией принадлежности:
с функцией принадлежности:
для каждого
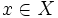 .
.Альтернативное представление операций над нечёткими множествами
Пересечение
В общем виде операция пересечения нечётких множеств определеляется следующим образом
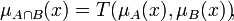
где функция T — это так называетмая T-норма. Ниже приведены частные примеры реализации T-нормы:
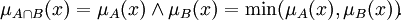
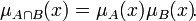
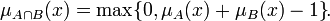
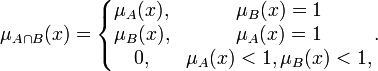
![\mu_{A\cap B}(x) = 1 - \min\{1,[(1 - \mu_A(x))^p + (1 - \mu_B(x))^p]^{1\over p}\}\!](/pictures/wiki/files/97/a46749e74f41e0bba8f2eae8b2565e7c.png) , для
, для 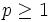 .
.
Объединение
В общем случае операция объединения нечётких множеств определеляется следующим образом
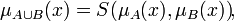
где функция S — S-норма (T-конорма). Ниже приведены частные примеры реализации S-нормы:
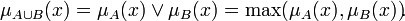
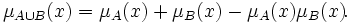

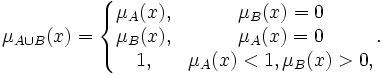
![\mu_{A\cup B}(x) = \min\{1,[\mu_A^p(x)+\mu_B^p(x)]^{1\over p}\}\!](/pictures/wiki/files/97/ab752813110f7a5172334aca3a61f914.png) , для
, для 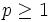 .
.
Связь с теорией вероятностей
Теория нечётких множеств в определенном смысле сводится к теории случайных множеств и тем самым к теории вероятностей. Последовательность теорем, описывающих это сведение, дана в монографиях [2, 3, 4]. Основная идея состоит в том, что значение функции принадлежности
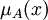 можно рассматривать как вероятность накрытия элемента
можно рассматривать как вероятность накрытия элемента 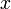 некоторым случайным множеством
некоторым случайным множеством 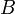 .
.Однако при практическом применении аппарат теории нечётких множеств обычно используется самостоятельно, выступая конкурентом к аппарату теории вероятностей и прикладной статистики.
Примеры
Литература
- Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. М.: Мир, 1976. 166c.
- Zadeh L.A. Fuzzy sets. — Information and Control, 1965, vol.8, N 3,pp.338-353.
- Батыршин И.З., Недосекин А.О., Стецко А.А., Тарасов В.Б., Язенин А.В., Ярушкина Н.Г. Теория и практика нечетких гибридных систем. Под ред. Н.Г. Ярушкиной. М.: Физматлит, 2007. ISBN 978-5-9221-0786-0
- Круглов В. В., Дли М. И., Голунов Р. Ю. Нечёткая логика и искусственные нейронные сети. Учеб. пособие. М.: Издательство Физико-математической литературы, 2001. - 224 c. ISBN 5-94052-027-8
- Кофман А. Введение в теорию нечетких множеств. М.: Радио и связь, 1982. - 432 с.
- Нечеткие множества и теория возможностей: Последние достижения. Под редакцией Р.Р. Ягера. - М.: Радио и связь, 1986.
- Орлов А. И. Задачи оптимизации и нечеткие переменные. М.: Знание, 1980. — 64 с.
- Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польского И. Д. Рудинского. М.: Горячая линия — Телеком, 2004. — 452 с. ISBN 5-93517-103-1
- Статьи и доклады Лотфи Заде http://zadeh.narod.ru/zadeh_papers.html
Ссылки
- Fuzzy.su - сайт о развитии теории и практическом применении нечетких множеств
- Международная ассоциация нечетких систем (International Fuzzy Systems Association)
- Российская ассоциация нечетких систем и мягких вычислений
- Нечеткая логика, мягкие вычисления и вычислительный интеллект
- Алексей Недосекин. Нечеткие множества, любовь моя
- Расширение языка CLIPS для работы с нечеткими множествами
См. также
- Носителем (суппортом) нечёткого множества
Wikimedia Foundation. 2010.

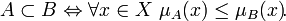
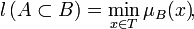



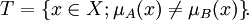
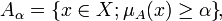
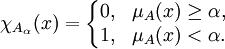
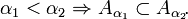
![\mu_A[\gamma x_1 +(1 - \gamma)x_2] \geq \langle\mu_A(x_1)\land \mu_A(x_2) = \min\{\mu_A(x_1), \mu_A(x_2)\}\rangle\!,](/pictures/wiki/files/55/700eeb69e78ca6fe29fc32831d4e0fc6.png)
![\mu_A[\gamma x_1 +(1 - \gamma)x_2] \leq \langle\mu_A(x_1)\lor \mu_A(x_2) = \max\{\mu_A(x_1), \mu_A(x_2)\}\rangle\!,](/pictures/wiki/files/101/ea86e10ed93dad24a72b1debaea5ca21.png)