Моделей теория

Теория моделей — это раздел математической логики, который занимается изучением связи между формальными языками и их интерпретациями, или моделями. Название теория моделей было впервые предложено Тарским в 1954 году. Основное развитие теория моделей получила в работах Тарского, Мальцева и Робинсона.

История возникновения

Теория моделей посвящена изучению фундаментальной взаимосвязи между синтаксисом и семантикой. При этом, первому в ней отвечает формальный язык, а второму — модель — математическая структура, допускающая некоторое описание этим языком. Теория моделей возникла как обобщение существующих подходов решения математематических проблем, связанных с алгеброй и математической логикой. Сами эти подходы существовали давно, но при этом долгое время не рассматривались во всей своей общности, в рамках одной логико-философской парадигмы. Естественным примером в этом контексте есть проблема, связанная с пятым постулатом Евклида о параллельности линий. Веками математикам не удавалось доказать его истинность, пока в XIX веке Бойяи и Лобачевский не построили неевклидову геометрию, показав тем самым, что постулат параллельности не может быть ни доказан, ни опровергнут. С точки зрения теории моделей, это означает, что система аксиом без пятого постулата допускает несколько различных моделей, то есть в этом случае — несколько вариантов реализации геометрии.

Таким образом, первоначальная теория моделей выросла из таких разделов математики как логика, универсальная алгебра, теория множеств в качестве обобщения и укрупнения существующих знаний. Поэтому первые результаты теории моделей появились задолго до её «официального» возникновения. Первым таким результатом принято считать^[1] теорему Лёвенгейма — Сколема (1915). Другим крупным результатом стала теорема компактности, доказанная Гёделем (1930) и Мальцевым (1936).

Классическая теория моделей первого порядка

Теория моделей для классической логики первого порядка является исторически первым и наиболее развитым примером теоретико-модельного подхода. В роли моделей здесь выступают множества, представляющие область возможных значений переменных. Функциональные символы интерпретируются как операции соответствующей арности над ними, а предикаты - как отношения (более подробно, см. Логика первого порядка, интерпретация).

Теорема компактности

Одним из важнейших инструментов теории моделей является теорема компактности, доказанная Мальцевым, которая утверждает, что множество формул первого порядка имеет модель тогда и только тогда, когда модель имеет каждое его конечное подмножество.

Название теоремы связано с тем, что она может быть сформулирована как утверждение о компактности стоуновского пространства.

Из теоремы компактности следует, что некоторые понятия не являются выразимыми в логике первого порядка. Например, понятия конечности или счётности не могут быть выражены никакими формулами первого порядка и даже их множествами: если множество формул имеет сколь угодно большие конечные модели, то оно имеет и бесконечную модель. Аналогично, теория, имеющая бесконечную модель, мощность которой не меньше мощности сигнатуры, имеет модели и любой большей мощности.

Теорема компактности находит применение для конструирования нестандартных моделей классических теорий, например, элементарной арифметики или математического анализа.

Теории и элементарная эквивалентность

Теория T — это множество замкнутных формул, замкнутое относительно выводимости, то есть если формула $\varphi$ следует из T, то $\varphi$ принадлежит T.

Теория, имеющая хотя бы одну модель, называется непротиворечивой, остальные теории — противоречивыми.

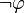Теория T называется полной, если для любой формулы $\varphi$ теория содержит $\varphi$ или $\lnot\varphi$. Если A — алгебраическая система, то множество истинных на A замкнутых формул образует полную теорию — теорию системы A, обозначаемую с помощью Th(A).

Если на алгебраических системах A и B истинны одни и те же замкнутые формулы, то A и B называются элементарно эквивалентными. Таким образом, A и B элементарно эквивалентны тогда и только тогда, когда они являются моделью одной и той же полной теории.

Если полная теория T имеет конечную модель A, то все модели теории T изоморфны A, в частности, все они содержат такое же количество элементов. Следовательно, для конечных алгебраических систем понятия элементарной эквивалентности и изоморфизма совпадают.

Подсистемы и теоремы Лёвенгейма — Скулема

Алгебраическая система B называется подсистемой алгебраической системы A, если 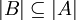$|B|\subseteq|A|$ и интерпретация каждого сигнатурного символа в B является ограничением его же интерпретации в A на множество | B | . Подсистема называется элементарной, если для любой формулы 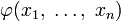$\varphi(x_1,\;\ldots,\;x_n)$ и для любых 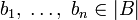$b_1,\;\ldots,\;b_n\in |B|$ выполнено: 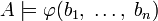$A\models\varphi(b_1,\;\ldots,\;b_n)$ тогда и только тогда, когда 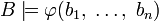$B\models\varphi(b_1,\;\ldots,\;b_n)$. Система A называется в этих случаях (элементарным) расширением системы B.

Если 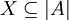$X\subseteq|A|$ — непустое множество, то среди всех подсистем A, включающих X, существует наименьшая, которая называется порожденной множеством X. Для элементарных подсистем в общем случае такое утверждение неверно.

Говорят, что теория T имеет термальные скулемовские функции, если для каждой формулы 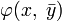$\varphi(x,\;\bar y)$ существует терм 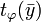$t_\varphi(\bar y)$ и из теории T следует формула 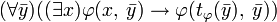$(\forall\bar y)((\exists x)\varphi(x,\;\bar y)\to \varphi(t_\varphi(\bar y),\;\bar y))$. Иначе говоря, если существует элемент, на котором формула 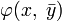$\varphi(x,\;\bar y)$ истинна, то в качестве этого элемента может быть взято 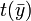$t(\bar y)$. Если теория имеет термальные скулемовские функции и A — ее модель, то любая подсистема A является элементарной. Каждая теория T имеет расширение T^s, имеющее термальные скулемовские функции. При этом каждая модель A теории T может быть обогащена до модели A^s теории T^s.

Теорема Лёвенгейма — Скулема «вверх» утверждает, что если A — алгебраическая система мощности не меньше α = | Th(A) | , то A имеет элементарные расширения любой мощности больше или равной α. Теорема Лёвенгейма — Скулема «вниз»: если A — алгебраическая система мощности α и β = | Th(A) | , то A имеет элементарные подсистемы любой мощности между β и α.

Аксиоматизируемость и устойчивость

Множество формул A называется множеством аксиом для теории T, если T является множеством следствий A. В частности, сама T является множеством аксиом для себя. Если для теории T существует конечное множество аксиом, то она называется конечно аксиоматизируемой.

Совокупности алгебраических систем называют классами. Класс алгебраических систем K называется аксиоматизируемым, если он является совокупностью моделей некоторой теории T. В этом случае множество аксиом для T называется также множеством аксиом для K. Класс K конечно аксиоматизируем тогда и только тогда, когда аксиоматизируемы сам K и его дополнение.

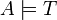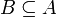Теория T называется устойчивой относительно надсистем (соответственно, подсистем), если для любой алгебраической системы A из $A\models T$ и $B\subseteq A$ (соответственно, 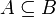$A\subseteq B$) следует, что 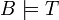$B\models T$. Теория T устойчива относительно подсистем тогда и только тогда, когда она аксиоматизируема посредством универсальных формул. Теория T устойчива относительно надсистем тогда и только тогда, когда она аксиоматизируема посредством экзистенциальных формул.

Теория T называется устойчивой относительно гомоморфизмов, если для любой алгебраической системы A из 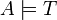$A\models T$ следует, что 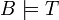$B\models T$, если B — гомоморфный образ A. Теория T устойчива относительно гомоморфизмов тогда и только тогда, когда она аксиоматизируема посредством позитивных формул (то есть формул, не содержащих импликацию и отрицание).

Цепи

Ультрапроизведения

Типы

Категоричность

Теория моделей высших порядков

Теория конечных моделей

Примечания

1. ↑ Кейслер Г., Чен Ч. Теория моделей. — М.: Мир, 1977, стр. 14