- Лемма Коши-Кантора
-
Лемма о вложенных отрезках или лемма Кантора — это фундаментальное утверждение в математическом анализе, связанное с полнотой поля вещественных чисел.
Формулировка
Пусть дана последовательность вложенных отрезков
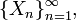 то есть
то есть ![X_n = [a_n,b_n],\; X_{n+1} \subset X_n,\; n\in \mathbb{N}.](/pictures/wiki/files/101/e73f02ee3c65a85d870a0af67bd4e38e.png) Тогда
Тогда- найдется хотя бы одна точка, принадлежащая всем этим отрезкам, то есть
- если длина отрезков стремится к нулю, то такая точка единственна:
Замечание
Отрезки в формулировке теоремы нельзя заменить на открытые интервалы. Например,
Доказательство
1)
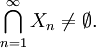
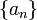 левее
левее 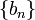 Тогда, из определения о вложенных отрезках
Тогда, из определения о вложенных отрезках 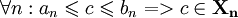
2)
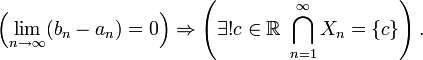
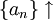 , что для любого
, что для любого 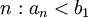 , следовательно существует
, следовательно существует 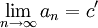
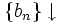 , что для любого
, что для любого 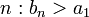 , и существует
, и существует 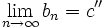
Так как мы доказываем единственность точки, следовательно пределы последовательностей в этой точке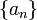 и
и 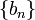 равны. Из этого следует,
равны. Из этого следует, 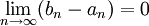
Как нам известно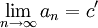 , а
, а 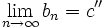 , то
, то
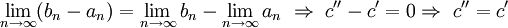
Что и требовалось доказать.
- найдется хотя бы одна точка, принадлежащая всем этим отрезкам, то есть
Wikimedia Foundation. 2010.