Ближний порядок

Ближний порядок — упорядоченность во взаимном расположении атомов или молекул в веществе, которая (в отличие от дальнего порядка) повторяется лишь на расстояниях, соизмеримых с расстояниями между атомами, то есть ближний порядок это наличие закономерности в расположении соседних атомов или молекул.

Ближним порядком в расположении атомов или молекул обладают, наряду с кристаллами,также аморфные тела и жидкости.

Радиальная функция распределения

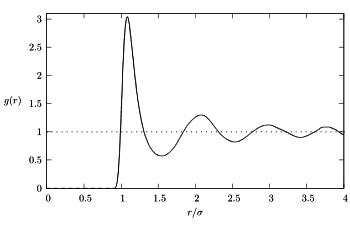Радиальная функция распределения $g(r)$ для жидкости Леннарда-Джонса вблизи тройной точки ($T^*=0{,}71, \; \rho^*=0{,}844$). Результат компьютерного моделирования.

Понятие ближнего порядка вводится через парную функцию распределения $f_2(\boldsymbol{r}_1, \boldsymbol{r}_2)$. Для этого $f_2$ представляется в виде

$f_2(\boldsymbol{r}_1, \boldsymbol{r}_2) = f_1(\boldsymbol{r}_1) f_1(\boldsymbol{r}_2) g(r_{12}),$

где $f_1(\boldsymbol{r})$ — одночастичная функция распределения, а $r_{12}=|\boldsymbol{r}_1-\boldsymbol{r}_2|$ — расстояние между двумя молекулами. Функция $g(r)$ носит название радиальной функции распределения. В основе такого представления парной функции распределения лежит предположение об однородности жидкости и изотропности потенциала взаимодействия.

Для идеального газа $g(r)=1$, то есть ближний порядок отсутствует, так как расположение каждой частицы в пространстве не зависит от расположения других частиц и двухчастичная функция распределения является просто произведением одночастичных $f_2(\boldsymbol{r}_1, \boldsymbol{r}_2) = f_1(\boldsymbol{r}_1) f_1(\boldsymbol{r}_2)$.

Однако для реального вещества ситуация иная. На рисунке показана характерная радиальная функция распределения для жидкости Леннарда-Джонса вблизи тройной точки. Она имеет осцилляции, затухающие с ростом $r$. Таким образом, вероятность найти молекулы на расстояниях, соответствующих локальным максимумам $g(r)$ больше, нежели на расстояниях, соответствующих локальным минимумам — в жидкости присутствует ближний порядок.

При увеличении температуры или уменьшении плотности ближний порядок становится всё менее отчётливым. Для разреженного реального газа $g(r)=\exp \left(-\textstyle{\frac{U(r)}{k_B T}} \right)$, $U(r)$ — потенциал парного взаимодействия частиц. Для этого случая остаётся только почти нулевая область при малых $r$ (соответствует конечным размерам молекул) и единственный пик (соответствует минимуму $U(r)$).

См. также

• Дальний порядок
• Химическая связь

Для улучшения этой статьи желательно?: Проставив сноски, внести более точные указания на источники. Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.