Контактный элемент

Касательное пространство $\scriptstyle T_xM$ и касательный вектор $\scriptstyle v\in T_xM$, вдоль кривой $\scriptstyle \gamma (t)$, проходящей через точку $\scriptstyle x\in M$

Касательное пространство к гладкому многообразию M в точке p — совокупность касательных векторов с введённой на ней естественной структурой линейного пространства. Касательное пространство к M в точке x обычно обозначается T_pM, или когда очевидно о каком многообразии идёт речь, просто T_p.

Совокупность касательных пространств во всех точках многообразия (вместе с самим многообразием) образует векторное расслоение, которое называется касательным расслоением. Соответственно, каждое касательное пространство есть слой касательного расслоения.

Также как у касательного вектора, существуют модификация понятия касательное пространство — касательное пространство в точке p подмногообразия.

В простейшем случае, когда гладкое многообразие гладко вложено в линейное пространство (что возможно всегда, согласно Теореме Уитни о вложении), каждое касательное пространство можно естественно отождествить с некоторым афинным подпространством объемлющего линейного пространства.

Определение через дифференцирование в точке

Пусть M — гладкое многообразие. Тогда касательным пространством назовем пространство дифференцирований в точке p. То есть пространство операторов X которые дают число Xf для каждой гладкой функции $f:M\to \R$, и обладающее следующими свойствами:

• Аддитивность: X(f + h) = Xf + Xh
• Правило Лейбница: $X(fh)=(Xf)\cdot h(p)+f(p)\cdot(Xh)$

Легко видеть, что на множестве всех дифференцирований в точке p можно ввести структуру линейного пространства:

(X + Y)f = Xf + Yf

$(k\cdot X)f=k\cdot(Xf).$

Свойства

• Касательное пространство n-мерного гладкого многообразия является n-мерным векторным пространством
• Для выбранной локальной карты 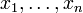$x_1,\dots, x_n$, операторы $X_if=\frac {\partial f}{\partial x_i}(p)$ представляют собой базис T_p, называемый голономным базисом.

Связанные определения

• Контактным элементом к многообразию в некоторой точке называется любая гиперплоскость касательного пространства в этой точке.

См. также

• Касательный вектор
• Кокасательное пространство
• Касательное расслоение