- Булева логика
-
- Не следует путать с булевой алгеброй.
Алгебра логики — раздел математической логики, в котором изучаются логические операции над высказываниями. Высказывания могут быть истинными и ложными.
Содержание
Определение
Высказывания строятся над множеством {B,
 ,
,  ,
,  , 0, 1}, где B — непустое множество, над элементами которого определены три операции:
, 0, 1}, где B — непустое множество, над элементами которого определены три операции: отрицание (унарная операция),
отрицание (унарная операция), конъюнкция (бинарная),
конъюнкция (бинарная), дизъюнкция (бинарная),
дизъюнкция (бинарная),
а также две константы — логический ноль 0 и логическая единица 1.
Дизъю́нкт — пропозициональная формула, являющаяся дизъюнкцией одного или более литералов (например
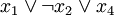 ). Конъюнкт — пропозициональная формула, являющаяся конъюнкцией одного или более литералов (например
). Конъюнкт — пропозициональная формула, являющаяся конъюнкцией одного или более литералов (например 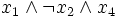 ).
).Аксиомы
1. ¬(¬x)=x, x=¬(¬x);
2. x*(¬x)=0;
3. x+1=1;
4. x+x=x, x=x+x+x;
5. x+0=x;
6. x*x=x, x=x*x*x;
7. x*0=0;
8. x*1=x;
9. x+(¬x)=1.Унарные логические операции x g1 (  )
)g2 (=) g3 (1) g4 (0) 0 1 0 1 0 1 0 1 1 0 g1(x) — отрицание/негация (g1(x) =
 x = x')
x = x')g2(x) — тождественная функция (g2(x) = x)
Бинарные логические операции x y f1 (  )
)f2 (  )
)f3 (  )
)f4 (  )
)f5 (  )
)f6 (  )
)f7 ( 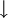 )
)f8 ( 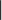 )
)0 0 0 0 1 0 1 1 1 1 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 0 0 1 1 1 1 1 1 0 1 1 0 0 x y f9 f10 f11 f12 f13 f14 f15 f16 0 0 0 0 1 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 1 0 0 1 1 0 1 0 1 1 0 0 0 0 1 1 1 0 Здесь 0 и 1 — тождественные нуль и единица соответственно,
f1(x, y) — конъюнкция (f1(x, y) = x&y = x
 y = x
y = x y = min(x, y)),
y = min(x, y)),f2(x, y) — дизъюнкция (f2(x, y) = x
 y = max(x, y)),
y = max(x, y)),f3(x, y) — эквивалентность (f3(x, y) = x
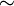 y = x
y = x y = x
y = x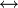 y),
y),f4(x, y) — сумма по модулю два (f4(x, y) = x
 y),
y),f5(x, y) — импликация от y к x (f5(x, y) = x
 y = x
y = x y),
y),f6(x, y) — импликация от x к y (f6(x, y) = x
 y = x
y = x y),
y),f7(x, y) — стрелка Пи́рса = функция Да́ггера = функция Ве́бба
(«антидизъюнкция») (f7(x, y) = x y).
y).f8(x, y) — штрих Ше́ффера («антиконъюнкция») (f8(x, y) = x
 y),
y),f9(x, y), f10(x, y) — инверсии импликаций f5 и f6,
f11—f14 — функции только одного аргумента,
f15, f16 — тождества.
Все вышеперечисленные функции называются логическими связками.
Логические операции
Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов:
- B = { Ложь, Истина }.
Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений, представленных в таблице справа, однако все они могут быть получены через суперпозицию трёх выбранных операций.
Опираясь на этот математический инструментарий, логика высказываний изучает высказывания и предикаты. Также вводятся дополнительные операции, такие как эквивалентность
 («тогда и только тогда, когда»), импликация
(«тогда и только тогда, когда»), импликация  («следовательно»), сложение по модулю два
(«следовательно»), сложение по модулю два  («исключающее или»), штрих Шеффера
(«исключающее или»), штрих Шеффера 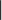 , стрелка Пирса
, стрелка Пирса 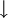 и другие.
и другие.Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция
 приобретает смысл вычитания из единицы;
приобретает смысл вычитания из единицы;  — немодульного сложения; & — умножения;
— немодульного сложения; & — умножения; 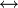 — равенства;
— равенства;  — в буквальном смысле сложения по модулю 2 (исключающее Или — XOR);
— в буквальном смысле сложения по модулю 2 (исключающее Или — XOR); 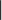 — непревосходства суммы над 1 (то есть A
— непревосходства суммы над 1 (то есть A 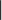 B = (A + B) <= 1).
B = (A + B) <= 1).Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено») и др. --
Свойства логических операций
- Коммутативность: x
 y = y
y = y x,
x, 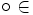 {&,
{&, 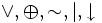 }.
}. - Идемпотентность: x
 x = x,
x = x, 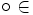 {&,
{&,  }.
}. - Ассоциативность: (x
 y)
y) z = x
z = x (y
(y z),
z), 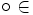 {&,
{&, 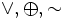 }.
}. - Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно:
- x
 (y
(y z) = (x
z) = (x y)
y) (x
(x z),
z), - x
 (y
(y z) = (x
z) = (x y)
y) (x
(x z),
z), - x
 (y
(y z) = (x
z) = (x y)
y) (x
(x z).
z).
- x
- Законы де Мо́ргана:
 (x
(x y) = (
y) = ( x)
x) (
( y),
y), (x
(x y) = (
y) = ( x)
x) (
( y).
y).
- Законы поглощения:
- x
 (x
(x y) = x,
y) = x, - x
 (x
(x y) = x.
y) = x.
- x
- Другие (1):
- x
 (
( x) = x
x) = x 0 = x
0 = x x = 0.
x = 0. - x
 (
( x) = x
x) = x 1 = x
1 = x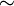 x = x
x = x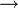 x = 1.
x = 1. - x
 x = x
x = x x = x
x = x 1 = x
1 = x 0 = x
0 = x 0 = x.
0 = x. - x
 1 = x
1 = x 0 = x
0 = x 0 = x
0 = x x = x
x = x x =
x =  x.
x. 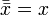 .
.
- x
- Другие (2):
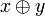 =
= 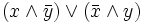 =
= 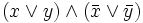 .
.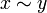 =
=  =
= 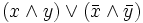 =
= 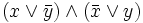 .
.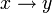 =
= 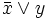 =
= 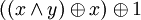 .
.
- Другие (3) (Дополнение законов де Мо́ргана):
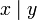 =
= 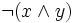 =
= 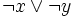 .
.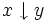 =
= 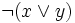 =
= 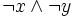 .
.
Существуют методы упрощения логической функции: например, Карта Карно, метод Куайна - Мак-Класки
История
Своим существованием наука обязана английскому математику Джорджу Булю, который исследовал логику высказываний. Первый в России курс по алгебре логики был прочитан П. С. Порецким в Казанском государственном университете
См. также
Ссылки
Логика Формальная Логические операции с понятиями
Изменение содержания понятия: отрицание • ограничение • обобщение • деление
Типы: Многозначная логика
Изменение объёма понятия: сложение • умножение • вычитаниеМатематическая
(теоретическая, символическая)Логические связки (операции) над высказываниями
Высказывание - построение над множеством {B,
2 константы: 0 • 1 ,
,  ,
,  , 0, 1}
, 0, 1}
В - непустое множество, над элементами которого определены три операции: конъюнкция ( или &,бинарная) • дизъюнкция (
или &,бинарная) • дизъюнкция ( ,бинарная) • отрицание (
,бинарная) • отрицание ( ,унарная)
,унарная)Прочее импликация (  )
)
Wikimedia Foundation. 2010.
