ЛАМИНАРНОЕ ТЕЧЕНИЕ

ЛАМИНАРНОЕ ТЕЧЕНИЕ

       

(от лат. lamina — пластинка, полоска), упорядоченное течение жидкости или газа, при к-ром жидкость (газ) перемещается как бы слоями, параллельными направлению течения. Л. т. наблюдается или у очень вязких жидкостей, или при течениях, происходящих с достаточно малыми скоростями, а также при медленном обтекании жидкостью тел малых размеров. В частности, Л. т. имеют место в узких (капиллярных) трубках, в слое смазки в подшипниках, в тонком пограничном слое, образующемся вблизи поверхности тел при обтекании их жидкостью или газом, и др. С увеличением скорости движения данной жидкости Л. т. в нек-рый момент переходит в турбулентное течение. При этом существенно изменяются все его св-ва, в частности структура потока, профиль скоростей, закон сопротивления. Режим течения жидкости характеризуется Рейнольдса числом Re. Когда значение Re меньше критич. числа Reкр, имеет место Л. т. жидкости; если Re > Reкр, течение становится турбулентным. Значение Reкр зависит от вида рассматриваемого течения. Так, для течения в круглых трубах ReKp »2300 (если характерной скоростью считать среднюю по сечению скорость, а характерным размером — диаметр трубы). При Reкр<2300 течение жидкости в трубе будет Л. т. Вязкое Л. т. жидкости в трубе определяется Пуазёйля законом.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

ЛАМИНАРНОЕ ТЕЧЕНИЕ

(от лат. lamina - пластинка) - упорядоченный режим течения вязкой жидкости (или газа), характеризующийся отсутствием перемешивания между соседними слоями жидкости. Условия, при к-рых может происходить устойчивое, т. е. не нарушающееся от случайных возмущений, Л. т., зависят от значения безразмерного Рейнольдса числа Re. Для каждого вида течения существует такое число R е _Кр, наз. нижним критич. числом Рейнольдса, что при любом Re<Re _кp Л. т. является устойчивым и практически осуществляется; значение R е _кр обычно определяется экспериментально. При R е>R е _кр, принимая особые меры для предотвращения случайных возмущений, можно тоже получить Л. т., но оно не будет устойчивым и, когда возникнут возмущения, перейдёт в неупорядоченное турбулентное течение. Теоретически Л. т. изучаются с помощью Навье - Стокса уравнений движения вязкой жидкости. Точные решения этих ур-ний удаётся получить лишь в немногих частных случаях, и обычно при решении конкретных задач используют те или иные приближённые методы.

Представление об особенностях Л. т. даёт хорошо изученный случай движения в круглой цилиндрич. трубе. Для этого течения R е _Кр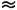2200, где Re= 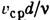( 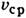- средняя по расходу скорость жидкости, d - диаметр трубы, 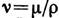- кинематич. коэф. вязкости, 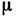- динамич. коэф. вязкости, 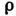- плотность жидкости). Т. о., практически устойчивое Л. т. может иметь место или при сравнительно медленном течении достаточно вязкой жидкости или в очень тонких (капиллярных) трубках. Напр., для воды (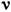=10^-6 м ²/с при 20° С) устойчивое Л. т. с 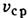=1 м/с возможно лишь в трубках диаметром не более 2,2 мм.

При Л. т. в неограниченно длинной трубе скорость в любом сечении трубы изменяется по закону 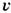-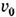(1 - -r²/ а²), где а - радиус трубы, r - расстояние от оси, 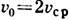- осевая (численно максимальная) скорость течения; соответствующий параболич. профиль скоростей показан на рис. а. Напряжение трения изменяется вдоль радиуса по линейному закону 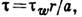где 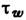= 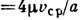- напряжение трения на стенке трубы. Для преодоления сил вязкого трения в трубе при равномерном движении должен иметь место продольный перепад давления, выражаемый обычно равенством P₁-P₂ 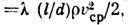где p₁ и р ₂ - давления в к.-н. двух поперечных сечениях, находящихся на расстоянии l друг от друга, 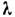- коэф. сопротивления, зависящий от 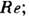для Л. т. 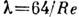. Секундный расход жидкости в трубе при Л. т. определяет Пуазейля закон. В трубах конечной длины описанное Л. т. устанавливается не сразу и в начале трубы имеется т. н. входной участок, на к-ром профиль скоростей постепенно преобразуется в параболический. Приближённо длина входного участка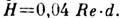

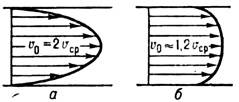
Распределение скоростей по сечению трубы: а - при ламинарном течении; б - при турбулентном течении.

Когда при 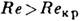течение становится турбулентным, существенно изменяются структура потока, профиль скоростей (рис., 6 )и закон сопротивления, т. е. зависимость 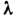от Re (см. Гидродинамическое сопротивление).

Кроме труб Л. т. имеет место в слое смазки в подшипниках, вблизи поверхности тел, обтекаемых маловязкой жидкостью (см. Пограничный слой), при медленном обтекании тел малых размеров очень вязкой жидкостью (см., в частности, Стокса формула). Теория Л. т. применяется также в вискозиметрии, при изучении теплообмена в движущейся вязкой жидкости, при изучении движения капель и пузырьков в жидкой среде, при рассмотрении течений в тонких плёнках жидкости и при решении ряда др. задач физики и физ. химии.

Лит.: Ландау Л. Д., Лифшиц Е. М., Механика сплошных сред, 2 изд., М., 1954; Лойцянский Л. Г., Механика жидкости и газа, 6 изд., М., 1987; Тар г С. М., Основные задачи теории ламинарных течений, М.- Л., 1951; Слезкин Н. А., Динамика вязкой несжимаемой жидкости, М., 1955, гл. 4 - 11. С. М. Тарг.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.